五大常用算法入门（三）——回溯算法

1. 写在前面

在正式介绍回溯算法的时候，我们先来回顾一下之前写的解答树的例子。

1.1 排列树
如果要生成 $1-n$ 的所有排列或者要生成含有 $n$ 个元素集合的一个排列，则我们会构造一棵排列树，例如当 $n=3$ 时：

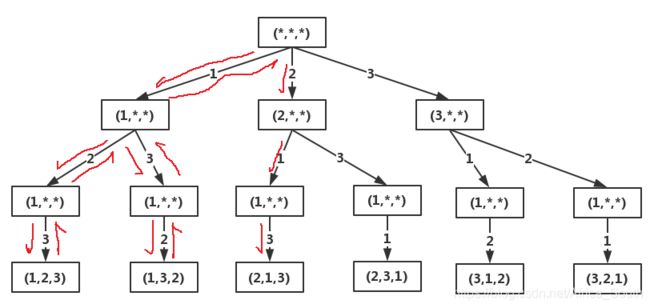
我们能得到 $3!=3\ast 2\ast 1=6$个叶子结点，每个叶子结点代表一个排列。一般的，对于含有n个元素的集合，我们最多有 $2^n$ 种不同的排列。

1.2 子集树
同样的，如果我们要枚举出含有n个元素S的子集，则我们会构造一个子集树。例如当集合 $S=\{1,2,3\}$时，我们有子集树：

上述子集树有 $2^n$ 个结点，每个结点表示一个子集。

或者有子集树：

上述子集树有 $2^n$ 个叶子结点，每个叶子结点表示一个子集的位向量。

1.3 解答树
而子集树和排列树是织回溯算法中的 解空间 的常见组织方式，下面用例子来说明。

2. 例子引入

2.1 排列树——八皇后问题

在棋盘上放置8个皇后，使得它们互不攻击。且每个皇后得攻击范围为同行、同列或者同对角线。如下图所示：(左图为攻击范围，右图为一可行解)

问题分析

• 最简单的想法是：从“64个格子中选择一个子集”，使得“子集中恰好有8个格子，且这8个格子不同列、不同行、不同对角线”，但是这样我们的解空间就含有 $2^{64}$ 个子集，太大。
• 第二种方案是“从64个格子中选择8个格子，使其满足条件”，这是一个排列组合生成问题，解空间有 $C_{64}^8=4.426\ast 10^9$ 种情况，还是太大。
• 第三种方案是，我们会在每一行放置一个皇后，则我们只需要求一个列的全排列使其满足条件即可，即令C[i]表示第i行皇后的列编号，则问题转换成生成一个 {1,2,3,4,5,6,7,8} 的列排列，使其满足条件，而8!=40320比方案1和2都要小。

问题实现
通过分析，我们将问题转换成了一个全排列生成问题，对于n个元素有 $n!$种情况，实际上，由于有限制条件，我们最后生成的排列树不一定有 $n!$ 个结点，以四皇后问题举例：

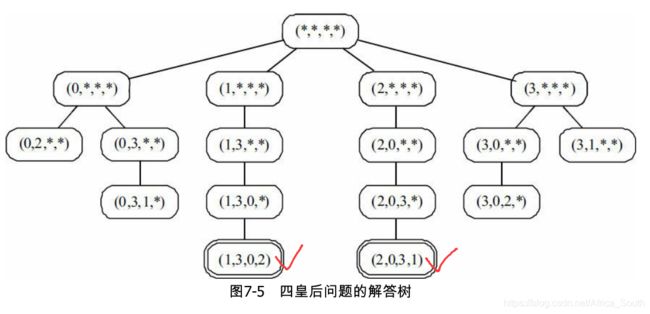
可以看到，最后的叶子结点只有2个。因为中间有些结点由于互不攻击条件限制而不同继续扩展。
在这种情况下，递归函数不再继续递归调用其本身，而是返回上一层调用，称之为回溯（backtracking）

实现方法1

void search1(int cur) {
	if (cur == n) {
		printMap(); // 打印结果
		return;
	}
	for (int i = 0; i < n; i++) {
		// 给第cur行选择一列i
		index[cur] = i; // 尝试cur行放i
		int ok = 1; // 合法
		for (int j = 0; j < cur; j++) {
			if (index[j] == i || index[cur] - cur == index[j] - j
				|| index[cur] + cur == index[j] + j) ok = 0; // 会攻击
		}// for
		if (ok) search1(cur + 1);
	}
}

上述写法每次尝试一个位置i时，都要遍历之前已经找到的列数是否存在攻击，即：$$\frac{cur-j}{index[cur]-index[j]}=\pm 1$$即$$cur-index[cur]=j-index[j]或cur+index[cur]=j+index[j]$$
其原理可有下图说明：

优化——空间换时间
实现方法1每次检查某个i是否合格时，都需要遍历已找到的列，而由上图可知，主对角线上x-y=C，此对角线上x+y=C，所以在判断某个行cur处列数i时候合格时，我们可以用两个数组来计算 cur + i 和 cur - i 是否出现过，即用数组vis[3][]来存储，其中

• 第一维表示已经放置的皇后占了哪些列；
• 第二维表示已经放置的皇后占了哪些主对角线；
• 第二维表示已经放置的皇后占了哪些次对角线；

// 八皇后问题求解
#include
#include
#include
using namespace std;

const int maxn = 20; // 最多20 x 20 个格子
const int maxd = maxn * 2 + 1; // 拿来记录状态

int vis[3][maxd]; 
// 0表示列，1表示主对角线，2表示次对角线
int n; // n 个皇后
int index[maxn]; // 第i个皇后所在的列数
int cnt; // 统计解答树中结点

void init() {
	memset(vis, 0, sizeof(vis));
	memset(index, 0, sizeof(index));
	cnt = 1; // 1 表示根结点
}
void printMap() {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (j == index[i]) printf("*");
			else printf("-");
		}// 行打印完成
		printf("\n");
	}
	printf("\n");
}
void search(int cur) {
	// 搜索cur位置
	if (cur == n) {
		printMap(); return;
	}
	for (int i = 0; i < n; i++) {
		if (!vis[0][i] && !vis[1][cur + i] && !vis[2][cur - i + n]) {
			cnt++;
			index[cur] = i;
			vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 1;
			search(cur + 1);
			vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 0;
		}
	}
}

int main() {
	while (cin >> n) {
		init();
		search(0);
		printf("%d皇后的内部结点%d\n", n, cnt);
	}
	return 0;
}

2.2 子集树——部分和问题

为了讨论子集树，我们举一个简单的例子，即给定n个正整数组成的集合A，判断能否从中选择某些数，使得其和为K。

问题分析：
此题很明显可以用子集树来构造解空间，比如位向量法，即设置一个数组vis[]，vis[i]=1表示选择第i个元素;否则不选，即解答树形式大概类似于下图：

当然不是每个结点都需要搜索，例如当搜索到某个结点时，当前和已经大于K了我们就没有再继续扩展该结点的必要了，因为集合A中元素全是正整数。

问题实现：

#include
#include
#include
#include
/*
输入 N 表示元素个数 1 <= N <= 20
输入 K 表示目标和，
若能找到这样的子集，则输出；否则输出NO
*/
using namespace std;

int a[20], vis[20];
int n, k;
int ok; // 是否有解
void dfs(int index, int sum) {
	// index表示当前位置,sum表示当前和
	if (index == n) {
		if (sum == k) {
			ok = 1;
			for (int i = 0; i < n; i++) {
				if (vis[i]) cout << a[i] << " ";
			}// for
			cout << endl;
		}
		return;
	}// if
	if (sum > k) return; // 剪枝
	vis[index] = 1; // 选当前位置
	dfs(index + 1, sum + a[index]); // 包含index
	vis[index] = 0; // 不选择当前位置
	dfs(index + 1, sum);
}
int main() {
	while (cin >> n >> k) {
		ok = 0;
		for (int i = 0; i < n; i++) cin >> a[i];
		memset(vis, 0, sizeof(vis));
		dfs(0, 0);
		if (ok == 0) cout << "No\n";
	}
	return 0;
}
/*
4 13
1 2 4 7
*/

3. 正式定义

再认真阅读了1和2后，我相信大部分人都对回溯法有了一些基础的认识，下面我们对回溯法进行正式介绍。

解决一个最无脑的方法就是生成——检验法，即列出所有候选解然后逐个检查，找出所需要的解，但是，当问题空间很大的时候，这种方法非常的耗时，所以我们需要对解空间搜索策略进行一些处理，其中一个方法就是——回溯法。

如果某问题的解可以由多个步骤得到，而每个步骤都有若干种选择（这些候选方案集可能会依赖于先前作出的选择），且可以用递归枚举法实现，则它的工作方式可以 用解答树来描述（例如子集树和排列树）。而这里所说的递归枚举法 就是我们的 回溯法，它的一般步骤如下：

• 1） 定义一个解空间，包含对问题的可行解；
• 2） 用适合搜索的方式组织解空间，例如树（排列树或子集树），或者图（迷宫问题）；
• 3） 利用深度优先搜索DFS搜索解空间，同时利用 剪枝函数 避免扩展无解的子结点。

即把问题的解空间转化成了图或者树的结构表示，然后使用深度优先搜索策略进行遍历，遍历的过程中记录和寻找所有可行解或者最优解,其类似于 图的深度优先搜索 和 树的后序遍历。

而我们的剪枝函数一般包含下面两类：

• 约束函数：即该结点违反了我们的约束条件，例如八皇后问题中的“不可攻击”条件；
• 界定函数：确定当前结点是否能产生比当前最优解还要好的解，若不能，则剪掉；或者我们要找和为k，但是当前结点的和已经超过了k（部分和问题）。

回溯法有一个很好的特性：
在进行搜索的同时产生问题的解，不用事先存储所有可能的解，所以回溯法需要的空间复杂度为 $O(从开始结点到终止结点的最长路径的长度)$。

4. 经典应用

排列树

• 旅行商问题

子集树

• 0/1背包问题

图解空间

• 迷宫问题

参考资料

• 《算法竞赛经典入门 第二版》 第7章 7.4节
• 《数据结构、算法与应用》 第20章