图论07—经过指定两点的最短路
经过两点(某路段)的最短路规划.
========================================================
function jingguoliangdianzuiduanlu(W)
clc
qidian=input('起点:');
zhongdian=input('终点:');
t1=input('经过点1:');%不是必须先经过点1
t2=input('经过点2:');
[p1 d1]=liangdianzuiduanlu(W,qidian,t1);
[p2 d2]=liangdianzuiduanlu(W,t1,t2);
[p3 d3]=liangdianzuiduanlu(W,t2,zhongdian);
dt1=d1+d2+d3;
[p4 d4]=liangdianzuiduanlu(W,qidian,t2);
[p5 d5]=liangdianzuiduanlu(W,t2,t1);
[p6 d6]=liangdianzuiduanlu(W,t1,zhongdian);
dt2=d4+d5+d6;
if dt1<=dt2
lujing=[p1 p2(2:length(p2)) p3(2:length(p3))];
d=dt1;
else
lujing=[p4 p5(2:length(p2)) p6(2:length(p3))];
d=dt2;
end;
lujing
d
========================================================
评:相当于求6次两点间最短路径,分两种情况:
(1)qidian-t1-t2-zhongdian
(2)qidian-t2-t1-zhongdian
每种情况求起点-中间点1,中间点1-中间点2,中间点2-终点共3个路径3个距离
缺点是有时会漏解(两条最短路距离相同,只会输出其中一条)
拓展:若需要,可增加至经过3点、4点等情况,只是排列组合情况复杂而已。
========================================================
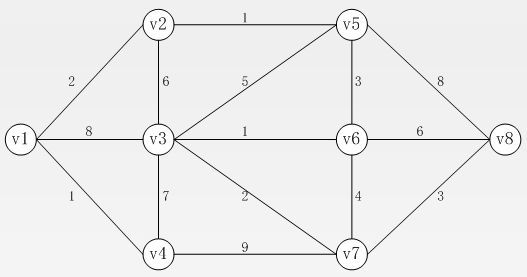
例:求下图中起点1,终点8,经过4和7的最短路。(可以想象成列车必须经停4、7站)
解:
(1)写权值矩阵
quanzhijuzhen=[ 0 2 8 1 Inf Inf Inf Inf
2 0 6 Inf 1 Inf Inf Inf
8 6 0 7 5 1 2 Inf
1 Inf 7 0 Inf Inf 9 Inf
Inf 1 5 Inf 0 3 Inf 8
Inf Inf 1 Inf 3 0 4 6
Inf Inf 2 9 Inf 4 0 3
Inf Inf Inf Inf 8 6 3 0]
(2)带入程序(格式整理后输出如下)
>> jingguoliangdianzuiduanlu(quanzhijuzhen)
起点:1
终点:8
经过点1:4
经过点2:7
lujing =
1 4 3 7 8
d =
13
说明:起点1,终点8,经过4和7的最短路径为1->4->3->7->8,最短距离为 13.