快速排序+改进版（邓俊辉老师讲授）

课程链接地址：https://www.bilibili.com/video/av22774520

快速排序是另一个分而治之排序算法。归并排序的重点在于合并，快速排序的重点在于分。（红色为每一次选取的候选轴点）

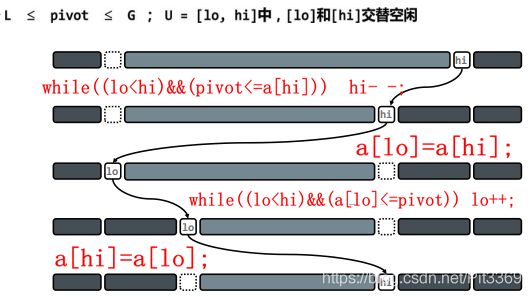
对于一个数组，起始为lo，结束为hi，轴点为pivot。通过每次选取不同的轴点，将轴点移动至某一位置，使得满足下述条件。

那么如何分呢？重点在于寻找轴点轴点需要满足的条件：其左侧元素都比其小，右侧元素都要比其大。如下图：

那么，快速排序就是使得所有元素逐个转换为轴点pivot，那么如何找到/构造这个轴点呢？

构造轴点

1. 任取一个数组元素设置为候选轴点pivot，那就随意点---选择a[0]
2. 中段U初始化为全集；比轴点小者归为前缀L，U左边界收缩；比轴点大者归为后缀G，U右边界收缩。

 

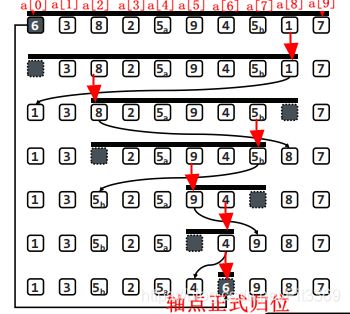
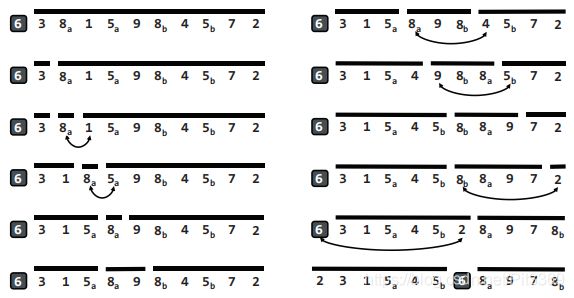
通过上面这个实例先来了解主要过程，再看代码估计就好一些了。

1. 首先，lo=0,hi=9，右侧选取a[0]=6为候选轴点，a[0]挖掉，作为前缀L的起始位置（因为a[0]作为轴点已经保存，则a[0]可以作为坑，待填）。默认选取第一个为候选轴点，默认从右侧a[hi-1]开始进行逐个检查。
2. a[hi=9]=7>轴点（6），归为后缀G，hi--；a[hi=8]=1<轴点（6），归为前缀L，lo++，a[8]连根拔起填入坑a[0]，a[8]变为坑。
3. a[lo=1]=3<轴点（6），归为前缀L，lo++；a[lo=2]=8>轴点（6），归为后缀G，hi--，a[2]连根拔起填入坑a[8]，a[2]变为坑。
4. ......依次根据上述规则，直至lo=hi时，轴点正式归位！

 

则可以归纳为：左右边界lo、hi交替向内收敛，逐个检查元素，与轴点比较，小的归为前缀，大的归为后缀，lo=hi时，即为轴点归位点！！！

综上，mid=6，a[6]=pivot=6；分的过程如图。详细代码如下。

void quickSort(int a[], int low, int high) 
{
  	if (low < high) 
	{
    	int m = partition(a, low, high); // O(N)
    	    // a[low..high] ~> a[low..m–1], pivot, a[m+1..high]
    	quickSort(a, low, m-1); // 递归地将左子阵列排序
    	    // a[m] = pivot 在分区后就被排序好了
    	quickSort(a, m+1, high); // 然后将右子阵列排序
  	}
}

int partition(int a[], int lo, int hi) 
{
   int pivot = a[lo]; //选取侯取轴点 
   while(lo

对于上述算法

最好的情况：每次划分接近平均（L、G都接近n/2），轴点总是接近中央(hi-lo)/2，此时达到O(logn)；

最坏的情况：每次划分都不均衡（比如轴点总是最大/最小元素），此时达到O(n^2)，与冒泡排序相当。

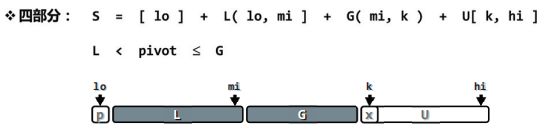
做出下列改进，根据L、G、U三者大小关系的不变性，将数组分为四个部分：

轴点最初还是选取a[0]，L左界是lo，L右界是mi，G左界是mi+1，G左界是mi，G右界是k，U左界是k，U右界是hi。

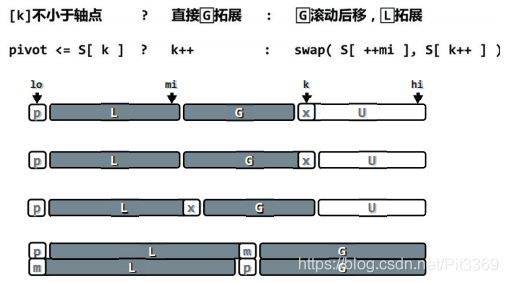
对于元素x逐个与轴点比较，若小于归为L，若大于归为G。当G区间足够大时，平滑式移动会比较复杂，在此采用滚动式移动比较简便，只要将x与G[mi+1]进行交换。为何能交换呢？因为G中元素均比x大，L中元素均比x小，这一条件始终满足。

遍历完成时，区间U会根据与轴点的大小，分别归入L、G，U会被完全分解，最终消失。最后一步，候选轴点与L右界进行交换，候选轴点归位，名副其实。

如上，可以归纳为：

 上述是第一次遍历的最终结果，其余情况类似。

int partition(int a[], int lo, int hi) 
{
	swap(a[lo],a[lo+rand()%(hi-lo+1)]);//随机交换，避免最坏情况的发生 
	int pivot = a[lo];
	int mi=lo;
	for(int i=lo+1;i<=hi;i++)//自左向右考察每个a[i] 
		if(a[i] a[low..m–1], pivot, a[m+1..high]
    	quickSort(a, low, m-1); // 递归地将左子阵列排序
    	// a[m] = pivot 在分区后就被排序好了
    	quickSort(a, m+1, high); // 然后将右子阵列排序
  	}
}