搜索算法入门

什么是搜索

搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况，从而求出问题的解的一种方法。现阶段一般有枚举算法、深度优先搜索、广度优先搜索、A*算法、回溯算法、蒙特卡洛树搜索、散列函数等算法。在大规模实验环境中，通常通过在搜索前，根据条件降低搜索规模；根据问题的约束条件进行剪枝；利用搜索过程中的中间解，避免重复计算这几种方法进行优化。
——百度百科

根据百度百科的定义，我们大致可以知道什么是搜索。同时，在上文的定义中在介绍了几种搜索方式的之后还介绍了几种搜索的优化方式，在本文中笔者将会介绍两种较为进阶的搜索方法：迭代加深（ID）搜索和启发式（A*）搜索。

---

常见的搜索优化

迭代加深（ID）搜索

对于迭代加深搜索，网络上并没有明确地阐明它的定义到底是什么，我们可以感性地理解一下迭代加深。

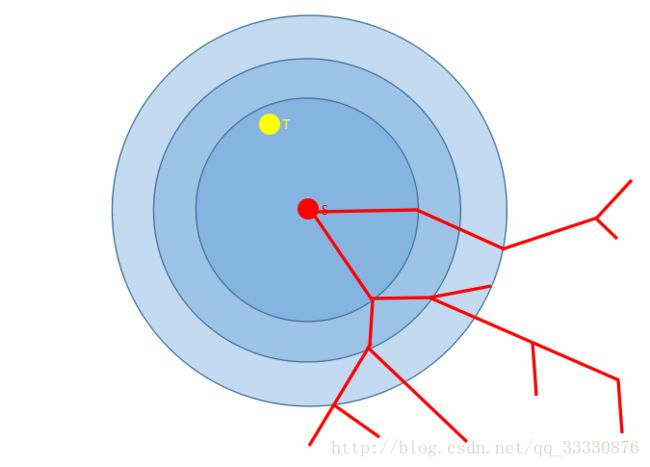
图示：



在图中，中间的红点（S）点为搜索的原点。对于某种题目（后文会说明），我们的搜索可以表示为如图所示的过程。

传统的DFS

传统的DFS在图中可以表示为从S点出发的红线所示的路径，这条路径可以用”不撞南墙不回头“来形容。因为没有搜到搜索的边界就不会停下来，而且搜索的层数越深，产生的冗余状态——既与正解无关的状态就产生地越多。

迭代加深搜索

而蓝色的半透明圆圈所示的就是一个迭代假设的过程，在限制了搜索深度的情况下在有限的深度内寻找最优解。迭代加深搜索适用于传统搜索后继状态多、深度上限较小的问题。在图中，迭代加深就可以避免传统DFS 搜得过深、搜得过窄 的情况。

经典问题

最经典的就是国际象棋问题，在复杂的中间局面里面你不会搜索得很深。而在残局中，有时你甚至会搜索到100层以上。

核心思想

有一位叫做 Bruce Moreland 的人这样说：

有一个思想，就是一开始只搜索一层，如果搜索的时间比分配的时间少，那么搜索两层，然后再搜索三层，等等，直到你用完时间为止。
这足以保证很好地运用时间了。如果你可以很快搜索到一个深度，那么你在接下来的时间可以搜索得更深，或许你可以完成。如果局面比你想象的复杂，那么你不必搜索得太深，但是至少有合理的着法可以走了，因为你不太可能连1层搜索也完不成。

伪代码

上述的叙述用代码可以表示为：

for (depth = 1; ; depth ++) {
    val = AlphaBeta(depth, -INFINITY, INFINITY);
    if (TimedOut()) break;
}

---

启发式（A*）搜索

启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。
——百度百科

图示


上图为传统搜索的图示（图摘）

---


上图为启发式（A*）搜索的图示（图摘）

传统的DFS

可以在第一张图中看出，传统的DFS搜索会搜出很多的冗余状态，导致程序的搜索量大大增加，降低程序效率。所以对比A*搜索，我们可以称传统搜索为”盲搜“。

启发式（A*）搜索

启发式搜索和核心就是它的估价函数，启发式搜索中的估价函数所起的作用可以感♂性地理解为”还有几步能到目标答案“，”距离正解还有多远“，……等等。一个启发式搜索的效率往往取决于估价函数的质量。对比与传统的DFS，启发式搜索可以被称为”有目标的搜索“。

所以说，A*搜索与其说是一种搜索的方法，不如说A*的估价函数是一种针对DFS的强力的剪枝。

---

相关例题

-

UVA 11212 Editing a Book

题目大意

给定一个由1到N的数字组成的组成的序列，问最少需要几步”剪切-粘贴“操作才能使该数列变为升序的有序数列。（1

大概思路

由题目可知，本题最坏的情况下也最多只会移动n-1步（虽然在实际情况中最多只有5步），所以可以在搜索的同时限制搜索层数，既使用迭代加深。

继续考虑每一层的情况，因为9！=362880，所以每一层的状态非常的庞大，因此我们可以采用A*剪枝。

考虑每一个序列后续不正确的数字个数h，每一次剪切最多3个数字后续数字发生改变，每次剪切最多可减少3个不正确的后续数字。所以在当前层d，最大层maxd时，最多可减少的不正确后续数字是3*(maxd-d)，若h>3*(maxd-d)，则剪枝。

代码

#include

const int maxn = 9;

int n,a[maxn];

inline bool End() {
    for(int i = 1; i < n; i++) {
        if(a[i] <= a[i-1]) return false;
    }
    return true;
}

inline int h() {
    int cnt = 0;
    for(int i = 1; i < n; i++)
        if(a[i] != a[i-1]+1) cnt++;
    return cnt;
}

int maxd;
const int intsz = sizeof(int);
const int asz = sizeof(a);

bool dfs(int d) {
    if(3*d + h() > 3*maxd) return false;
    if(End()) return true;

    int old[maxn]; //保存a
    memcpy(old,a,asz);
    int b[maxn]; //剪切板

    for(int i = 0; i < n; i++) if( i == 0 || old[i] != old[i-1] + 1) //策略3 选择尽量长的连续片段 剪切的起点
    for(int j = i; j < n; j++) {  //不同选取片段可以不连续
        while(j+1 < n && old[j+1] == old[j] + 1)j++ ;
        memcpy(b,old+i,intsz*(j-i+1));  //剪切移动片段
        for(int k = j+1;k < n;k++){ //由于对称性，只要往后贴就行了
            while(k+1 < n && old[k+1] == old[k] + 1)k++;//不破坏连续序列
            memcpy(a+i,old+j+1,intsz*(k-j));
            memcpy(a+i+k-j,b,intsz*(j-i+1));
            if(dfs(d+1))return true; //恢复
            memcpy(a,old,asz);
        }
    }
    return false;
}

inline int solve() {
    if(End())return 0;
    for(maxd = 1; maxd < 5 ;maxd++)
        if(dfs(0)) return maxd;
    return 5;
}
int main() {
    int Cas = 0;
    while(~scanf("%d",&n)&&n) {
        for(int i = 0; i < n; i++)
            scanf("%d",a+i);
        int ans = solve();
        printf("Case %d: %d\n",++Cas,ans);
    }
    return 0;
}