0x43.数据结构进阶 - 线段树

声明：
本系列博客是《算法竞赛进阶指南》+《算法竞赛入门经典》+《挑战程序设计竞赛》的学习笔记，主要是因为我三本都买了 按照《算法竞赛进阶指南》的目录顺序学习，包含书中的少部分重要知识点、例题解题报告及我个人的学习心得和对该算法的补充拓展，仅用于学习交流和复习，无任何商业用途。博客中部分内容来源于书本和网络（我尽量减少书中引用），由我个人整理总结（习题和代码可全都是我自己敲哒）部分内容由我个人编写而成，如果想要有更好的学习体验或者希望学习到更全面的知识，请于京东搜索购买正版图书：《算法竞赛进阶指南》——作者李煜东，强烈安利，好书不火系列，谢谢配合。

---

下方链接为学习笔记目录链接（中转站）

学习笔记目录链接

---

ACM-ICPC在线模板

---

好久没有写线段树了。线段树可好玩了呢！正好这次从基础再过一遍
具体的基础知识可以看《算法竞赛进阶指南》哟

一、基础线段树

线段树要保证数组长度不小于4N

首先定义左右儿子

#define ls (p<<1)
#define rs (p<<1|1)

线段树的建树

struct SegmentTree{
    int l,r;
    int dat;//最大值
    int sum;//和
}t[N<<2];

void build(int p,int l,int r){
    t[p].l = l;t[p].r = r;
    if(l == r){
        t[p].dat = a[r];
        return ;
    }
    int mid = (l + r) / 2;
    build(ls,l,mid);
    build(rs,mid+1,r);
    t[p].dat = max(t[ls].dat,t[rs].dat);
    t[p].sum = t[ls].sum + t[rs].sum;
}
int n;
int main(){
    build(1,1,n);
}

线段树的单点修改

void change(int p,int x,int val){
    if(t[p].l == t[p].r){
        t[p].dat = t[p].sum = val;
        return ;
    }
    int mid = (t[p].l + t[p].r) / 2;
    if(x <= mid)change(ls,x,val);
    else change(rs,x,val);
    t[p].dat = max(t[ls].dat,t[rs].dat);
    t[p].sum = t[ls].sum + t[rs].sum;
}

线段树的区间查询

int ask_max(int p,int l,int r){
    if(l <= t[p].l && r >= t[p].r)
        return t[p].dat;
    int mid = (t[p].l + t[p].r) / 2;
    int val = -(1<<30);
    if(l <= mid)val = max(val,t[ls].dat);
    if(r > mid)val = max(val,t[rs].dat);
    return val;
}

线段树的延迟标记（懒惰标记）

1.POJ3486 $ASimpleProblemwithIntegers$

…

The sums may exceed the range of 32-bit integers.
Source
…

题意：一行序列，每次操作把一个区间里的每个数都加上一个数，或者查询一个区间的和。

模板题，
注意数据范围会爆int，记得开long long 。

#include
#include
#include
#include
#include
#include
#include
#include

#define ls (p<<1)
#define rs (p<<1|1)

#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5+7;
const int M = 2007;

struct SegmentTree{
    int l,r;
    ll sum;//总和
    ll lz_add;//增量延迟标记
    #define tl(x) tree[x].l
    #define tr(x) tree[x].r
    #define tsum(x) tree[x].sum
    #define lza(x) tree[x].lz_add
}tree[N<<2];

int a[N],n,m;

void build(int p,int l,int r){
    tl(p) = l,tr(p) = r;
    if(l == r) {
        tsum(p) = a[r];
        return ;
    }
    int mid = (l + r) / 2;
    build(ls,l,mid);
    build(rs,mid+1,r);
    tsum(p) = tsum(ls) + tsum(rs);
}

void push_down(int p){//向下更新一层
    if(lza(p)){
        tsum(ls) += lza(p)*(tr(ls) - tl(ls) + 1);
        tsum(rs) += lza(p)*(tr(rs) - tl(rs) + 1);
        lza(ls) += lza(p);//注意是+=
        lza(rs) += lza(p);
        lza(p) = 0;
    }
}

void change(int p,int l,int r,int d){
    if(l <= tl(p) && r >= tr(p)){
        tsum(p) += (ll)d * (tr(p) - tl(p) + 1);//差多少补多少
        lza(p) += d;
        return ;
    }
    push_down(p);
    int mid = (tl(p) + tr(p)) / 2;
    if(l <= mid)change(ls,l,r,d);
    if(r > mid)change(rs,l,r,d);
    tsum(p) = tsum(ls) + tsum(rs);
}

ll ask(int p,int l,int r){//ask和change的时候都要push_down，因为要直接用下一层
    if(l <= tl(p) && r >= tr(p))
        return tsum(p);
    push_down(p);
    int mid = (tl(p) + tr(p)) / 2;
    ll val = 0;
    if(l <= mid)val += ask(ls,l,r);
    if(r > mid)val += ask(rs,l,r);
    return val;
}

int main()
{
    cin>>n>>m;
    over(i,1,n)
    scanf("%d",&a[i]);
    build(1,1,n);
    while(m--){
        char ch[2];
        int l,r,d;
        scanf("%s%d%d",ch,&l,&r);
        if(ch[0] == 'C'){
            scanf("%d",&d);
            change(1,l,r,d);
        }
        else printf("%lld\n",ask(1,l,r));
    }
    return 0;
}

二、扫描线法

2.POJ1151 $Atlantis$

线段树扫描线的应用

我们尝试设想有一条无限高的竖线左往右扫过这个并集图形，按照每一个矩形的的左右边界，我们可以将这个并集图形分为2n 段，对于两两相邻的部分，我们可以分别计算面积，这样就得到了整个并集图形的面积。

如图，我们就是把每个矩形的左右边界提了出来，就变成了这样一些线段。
那么我们需要这些量化记录下来：每个四元组(x,y1,y2,1/−1)分别代表了一条线段，x是线段的横坐标，(y1,y2)是线段上下端点的纵坐标，1/−1代表了这条线段是矩形的左边界还是右边界。

显然，我们只需要把这些线段按照横坐标排序，对于一次遍历来说，两两线段之间的距离是已知的。那么我们需要解决的问题就是纵坐标的影响范围。
我们不妨把纵坐标都取出来，离散化映射到[1,T]之间的T个整数值，并将这些纵坐标表示为T−1段，其中第i段代表了第i个纵坐标和第i+1个纵坐标之间的部分，然后，我们设立数组ci代表第i段被覆盖的次数。

这样，我们就可以用如下的算法流程计算矩形的面积：

1. 对于每一个线段，将其的k值累加到这个线段对应的若干个纵坐标区间
2. 计算面积：所有T−1个纵坐标区间对应的c值大于零的就说明这些部分的区间还存在，将存在的区间的长度累加起来，乘上当前线段与下一条线段之间的横坐标之差就是这两条线段之间的面积。

显然，这里需要我们维护一个区间内的区间加法，区间求和，这个就是线段树的事情了。

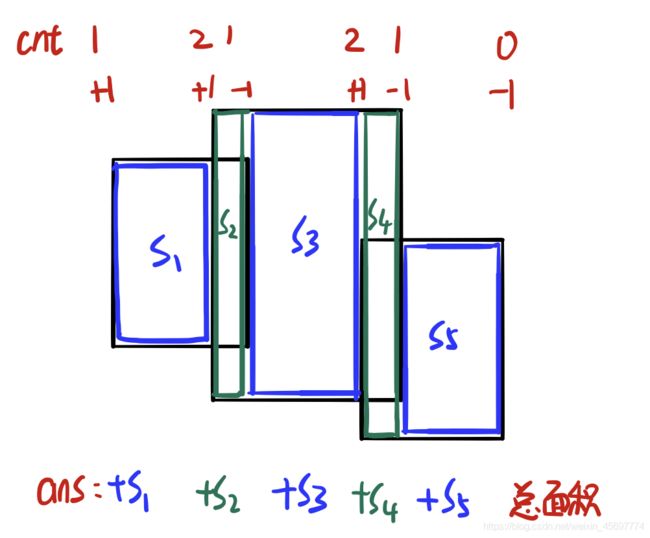
由于本题中的区间修改成对出现，互相抵消，所以我们可以不写带有lazytag的线段树。我们在线段树的每一个节点上维护两个值cnt和len，cnt代表这段区间被覆盖的次数，如果cnt>0则当前区间的len等于当前区间的纵坐标长度，反之lenp=lenp∗2+lenp∗2+1。那么对于每一次区间修改，我们直接在线段树上改cnt的值即可，并沿路更新len值即可。

/*POJ 1151 Atlantis*/
#include
#include
#include
#include
#include
#include
#include
#include

#define ls (p<<1)
#define rs (p<<1|1)

#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5+7;
const int M = 2007;

struct line{
    double x,y1,y2;
    int f;
    bool operator<(const line &t)const{
        return x < t.x;
    }
}a[N<<1];

struct SegmentTree{
    int l,r;
    double cnt;
    double len;
    #define tl(x) tree[x].l
    #define tr(x) tree[x].r
    #define tcnt(x) tree[x].cnt
    #define tlen(x) tree[x].len
}tree[N<<3];

int n,T,tot,val[N<<1][2];
double raw[N<<1],ans;

inline void build(int p,int l,int r){
    tl(p) = l;
    tr(p) = r;
    if(l == r)return ;
    int mid = (l+r) / 2;
    build(ls,l,mid);
    build(rs,mid+1,r);
}

inline void push_up(int p){
    if(tcnt(p) > 0)tlen(p) = raw[tr(p) + 1] - raw[tl(p)];
    else if(tl(p) == tr(p))tlen(p) = 0;
    else tlen(p) = tlen(ls) + tlen(rs);
}

void updata(int p,int l,int r,int v){
    if(l <= tl(p) && r >= tr(p)){
        tcnt(p) += v;
        push_up(p);
        return ;
    }
    int mid = (tl(p) + tr(p)) / 2;
    if(l <= mid)updata(ls,l,r,v);
    if(r > mid)updata(rs,l,r,v);
    push_up(p);
}

int main()
{
    while(cin>>n && n){
        ans = tot = 0;
        over(i,1,n){
            double x1,x2,y1,y2;
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            a[2*i-1] = (line){x1,y1,y2,1};//奇和偶，左和右
            a[2*i] = (line){x2,y1,y2,-1};
            raw[++tot] = y1;
            raw[++tot] = y2;
        }
        sort(a+1,a+1+2*n);
        sort(raw+1,raw+1+tot);
        tot = unique(raw+1,raw+1+tot) - (raw+1);//注意+1因为从1开始的
        over(i,1,2*n){
            val[i][0] = lower_bound(raw+1,raw+1+tot,a[i].y1) - raw;
            val[i][1] = lower_bound(raw+1,raw+1+tot,a[i].y2) - raw;
        }
        build(1,1,tot);
        over(i,1,2*n){
            updata(1,val[i][0],val[i][1] - 1,a[i].f);
            ans += (a[i+1].x - a[i].x) * tlen(1);
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",++T,ans);
    }
    return 0;
}

POJ 2482-Stars in Your Window(经典扫描线变式)

题目大意：给出n个星星的坐标，每个星星有一个亮度，给出一个矩形的长和宽，问矩形能包括的星星的最大亮度和（不包括边框）。

https://fanfansann.blog.csdn.net/article/details/106725096

三、动态开点和线段树合并

动态开点

在一些计数问题中，线段树用于维护值域（一段权值范围），这样的线段树被称之为权值线段树。为了降低空间复杂度，我们可以不建出整棵树的结构，而是在最初只建立一个根结点，代表整个区间，当需要访问线段树的某棵子树（某个子区间）时，在建立代表这个区间的结点，这种方法就是动态开点的线段树。

这里使用了指针来代表子结点，并在递归访问的过程中区间作为参数来传递。

int tot;
struct Seg{
    int lc,rc;
    int dat;//区间最大值
    #define trl(x) tree[x].lc
    #define trr(x) tree[x].rc
    #define tdat(x) tree[x].dat
}tree[N<<1];

int build(){
    tot++;
    trl(tot) = trr(tot) = tdat(tot) = 0;
    return tot;
}
//将val位置上的值加上delta
void Insert(int p,int l,int r,int val,int delta){
    if(l == r){
        tdat(p) += delta;
        return ;
    }
    int mid = (l + r) / 2;
    if(val <= mid){//要往左边走
        if(!trl(p))//但是左边没有
            trl(p) = build();//动态开点//返回的是tot，也就是指针
        Insert(trl(p),l,mid,val,delta);
    }
    else {
        if(!trr(p))//同上
            trr(p) = build();
        Insert(trr(p),mid+1,r,val,delta);
    }
    tdat(p) = max(tdat(trl(p)),tdat(trr(p)));
}
int root,n;
int delta,val;
int main()
{
    tot = 0;
    root = build();//根节点
    Insert(root,1,n,val,delta);
}

线段树合并

int Merge(int p,int q,int l,int r){
    if(!p)return q;//一旦有一个为空就return
    if(!q)return p;
    if(l == r){//到达叶子结点
        tdat(p) += tdat(q);
        return p;//规定合并到p处并返回p
    }
    int mid = (l + r) / 2;
    trl(p) = Merge(trl(p),trl(q),l,mid);
    trr(p) = Merge(trr(p),trr(q),mid+1,r);
    tdat(p) = max(tdat(trl(p)),tdat(trr(p)));
    return p;
}

一个写的很棒的线段树教程
cppblog.com/menjitianya/archive/2016/02/25/212891.html