Dijkstra算法（matlab)

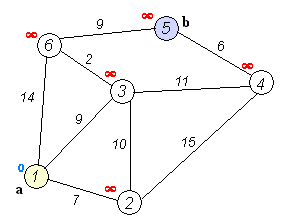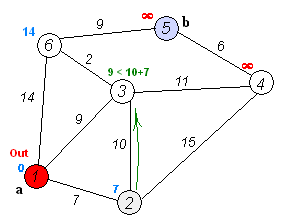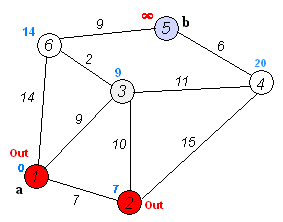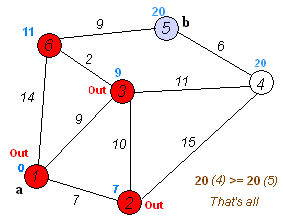
Dijkstra算法是寻找最短路径的一种搜索算法，由荷兰科学家提出。

算法描述：通过为每个节点保留目前为止所找到的从s到e的最短路径。为了记录最佳路径轨迹，记录路径上每个节点的前趋，通过回溯法找出最短路径轨迹。

在网上搜索一些版本的Matlab实现方法，感觉都有些毛病。经过修改，得到比较好的效果。

function [ distance path] = Dijk( W,st,e )
%DIJK Summary of this function goes here
%   W  权值矩阵   st 搜索的起点   e 搜索的终点
n=length(W);%节点数
D = W(st,:);
visit= ones(1:n); visit(st)=0;
parent = zeros(1,n);%记录每个节点的上一个节点

path =[];

for i=1:n-1
    temp = [];
    %从起点出发，找最短距离的下一个点，每次不会重复原来的轨迹，设置visit判断节点是否访问
    for j=1:n
       if visit(j)
           temp =[temp D(j)];
       else
           temp =[temp inf];
       end
       
    end
    
    [value,index] = min(temp);
   
    visit(index) = 0;
    
    %更新 如果经过index节点，从起点到每个节点的路径长度更小，则更新，记录前趋节点，方便后面回溯循迹
    for k=1:n
        if D(k)>D(index)+W(index,k)
           D(k) = D(index)+W(index,k);
           parent(k) = index;
        end
    end
    
   
end

distance = D(e);%最短距离
%回溯法  从尾部往前寻找搜索路径
t = e;
while t~=st && t>0
 path =[t,path];
  p=parent(t);t=p;
end
path =[st,path];%最短路径


end

测试：

测试用例1

W=[0 50 inf 40 25 10
    50 0 15 20 inf 25
    inf 15 0 10 20 inf 
    40 20 10 0 10 25
    25 inf 20 10 0 55
    10 25 inf 25 55 0];

[distance,path]=Dijk(W,1,4);

>> distance


distance =


    35


>> path


path =


     1     6     4

从节点1到节点4最短距离路径为1-->6-->4, 最短距离为35

测试用例2

W=[0 1 3 4
    1 0 2 inf
    3 2 0 5
    4 inf 5 0];

[distance,path]=Dijk(W,2,4);

>> distance


distance =


     5


>> path


path =


     2     1     4
从节点2到节点4最短距离路径为2-->1-->4, 最短距离为5

java版dijkstra

import java.util.HashMap;
import java.util.Map;

/**
 * Created by zhangjackie on 18/5/2.
 */
public class DijkstraShortPath {
    private static final int N = 1000;
    private static int[][] graph = {
            {0, 7, 9, N, N, 14},
            {7, 0, 10, 15, N, N},
            {9, 10, 0, 11, N, 2},
            {N, 15, 11, 0, 6, N},
            {N, N, N, 6, 0, 9},
            {14, N, 2, N, 9, 0}
    };

    private static void dijkstra(int vstart, int[][] graph) {
        int n = graph.length;
        int[] dist = new int[n];
        boolean[] visit = new boolean[n];
        int[] prev = new int[n];
        Map path = new HashMap();
        int vnear = vstart;

        //初始化
        for (int i = 0; i < n; i++) {
            dist[i] = graph[vstart][i];
            visit[i] = false;
            prev[i] = vstart;
        }

        visit[vstart] = true;


        for (int i = 1; i < n; i++) {
            int min = N;
            //寻找最近的节点
            for (int j = 0; j < n; j++) {
                if (!visit[j] && dist[j] < min) {
                    min = dist[j];
                    vnear = j;
                }
            }

            visit[vnear] = true;

            //更新dist,记录前一执行节点
            for (int k = 0; k < n; k++) {
                int minDist = min + graph[vnear][k];
                if (!visit[k] && minDist < dist[k]) {
                    dist[k] = minDist;
                    prev[k] = vnear;
                }
            }
        }

        //打印最短路径
        for (int i = 0; i < n; i++) {
            int preprev = prev[i];
            path.put(i,Integer.toString(i));
            while (preprev != vstart) {
                String oldpath = path.get(i);
                path.put(i, preprev + "->" + oldpath);
                preprev = prev[preprev];
            }

            String oldpath = path.get(i);
            path.put(i,  vstart +"->" + oldpath);
        }

//        System.out.println(Arrays.toString(dist));
        for (int i = 0; i < n; i++) {
//            System.out.println("v" + vstart + "...v" + prev[i] + "->v" + i + ", s=" + dist[i]);
            System.out.println(path.get(i)  + ", s=" + dist[i]);
        }

    }


    public static void main(String[] args) {
        dijkstra(3, graph);
    }

}