算法：螺旋折线问题

引言：2018蓝桥杯 Java B 个人解析
该题方法很多，就不列举了。

题目7：螺旋折线

如图p1所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】
X和Y

对于40%的数据，-1000 <= X, Y <= 1000
对于70%的数据，-100000 <= X， Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】
输出dis(X, Y)

【输入样例】
0 1

【输出样例】
3

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是：Main，否则按无效代码处理。

---

我在做的时候首先想到的就是把原图分为4个象限，不同位置的点使用不同的函数计算。
有个规律，每一圈，左下角的点的值都是所在边的长度的平方。
例如：dis（-1，0）=1,dis(-2,-1)=9.
下面我给出部分dis值的参照表，方便参考。

坐标	dis值
0,0	0
-1,0	1
-1,1	2
0,1	3
1,1	4
1,0	5
1,-1	6
0,-1	7
-1,-1	8
-2,-1	9
……	……
-6,-1	125
……	……
2,8	250
……	……

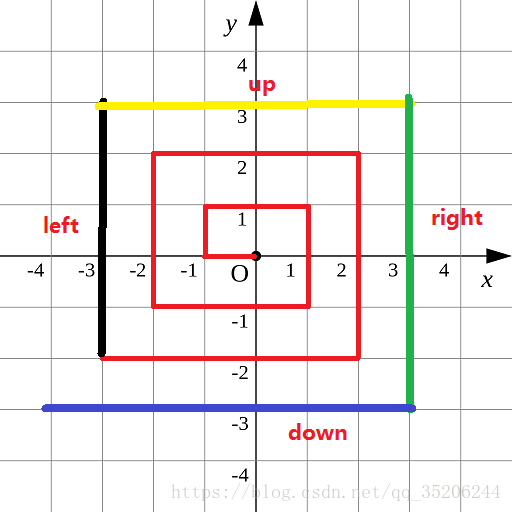
方法一、
如图2所示，将折线按颜色分为4个区域，对应的计算函数为left，up，right，down。
左下角点（-3，-2）的值恰为其所在边长度的平方，也就是（2*（-x）-1）^2。
那么，该边上其他点的dis值就是该点到左下角点的距离加上左下角点的值，dis（x，x+1）。
左上角点有其位置的特殊性，坐标均为（x，-x），因此其值恰为dis（左下角点）+|x|。
有个距离函数：Point.distance(x1,y1,x2,y2);返回两点的距离的double值。
其他边依次类推，上一边的最后一个点，也是下一边的第一个点。

import java.awt.Point;
import java.util.Scanner;


public class Main {

	public static int left(int x,int y){
		
		if((x+1)==y)return(int)(2*(-x)-1)*(2*(-x)-1);
		//左下角坐标，dis(x,y)=(2*(-x)-1)^2
		if(y==-x)
		return (int)((2*(-x)-1)*(2*(-x)-1)+Point.distance(x, y, x, x+1));
		//左上角坐标,dis(x,y)=dis(左下角)+point.distance(左下角,左上角);
		//左下角-左上角之间的其他任意点的值等于左下角的值加上该点与左下角的距离
		if(y!=x||y!=-x)			
		return(int) (left(x,x+1)+Point.distance(x, y, x, x+1));
		return 0;
	
	}
	public static int up(int x,int y){
		if(x==y)return(int) (left(-x,y)+Point.distance(x,y,-x,y));
		if(x!=-y||x!=y)
		return(int) (left(-y,y)+Point.distance(x, y, -y, y));
		return 0;
	}
	public static int right(int x,int y){
		if(y!=x||y!=-x)return (int)(up(x, x)+Point.distance(x, y, x, x));
		return 0;
		
	}
	public static int down(int x,int y){
		if(x!=-y||x!=y)
		return (int) (right(-y,y)+Point.distance(x, y, -y, y));
		return 0;
		
	}
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int x=sc.nextInt();
		int y=sc.nextInt();
		int sum=0;
			int start = (int) System.nanoTime();
		if(x<0 && (y>=x+1&&y<=-x)) {//left
			sum = left(x,y);
		}
		if(x>0 && (y>=-x&&y<=x)) {//right
			sum = right(x, y);
		}
		if(y>0 && (x>=-y&&x<=y)) {//up
			sum = up(x, y);
		}
		if(y<0 && (x>=y-1&&x<=-y)) {//down
			sum = down(x, y);
		}
		int end = (int) System.nanoTime();
		System.out.println("耗时："+(end-start)+"ns(或 "+(end-start)/1000000+" ms)");
		System.out.println(sum);
		System.out.println(sum);
	}

}

方法二、

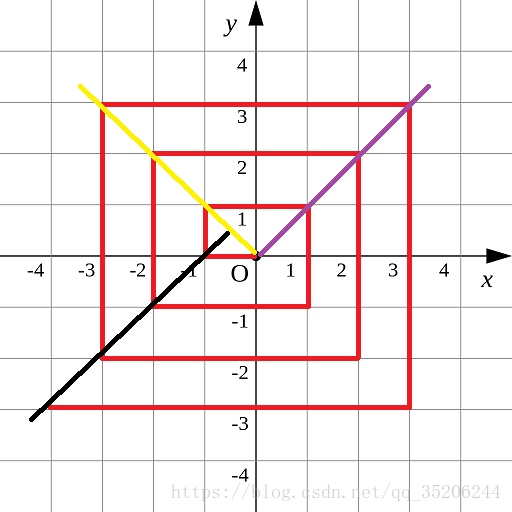
大致思想为：将折线分为3部分，①：黑线-黄线之间 ②：黄线-紫线之间 ③： 紫线-黑线之间
同方法一所述，区域①部分点的dis值均可基于左下角点计算，即满足（x，x+1）（x<0)的点。
区域②可基于右上角点减去两点之间距离计算。左上角点（x==y）的dis值满足（x+y）^2。
区域③即可通过左下角点和右上角点结合计算。
方法三、

---

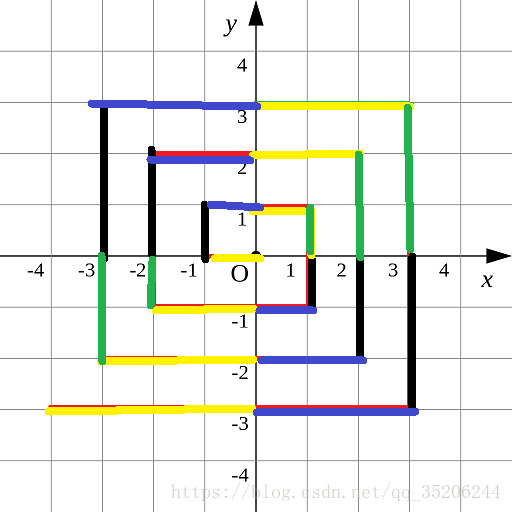
感谢评论区林鸿清读者的勘误，算法思想及其实现是正确的，对于没有返回预期输出的问题，原因是main函数中的判断有误，现修改中。

---

2019年8月14日 22:56:46

上面的错误引申出一个新问题，如何判断一个点在left，up，right，down某个区域？
即，这个点是x<0,平行于y轴，还是x>0，平行于y轴，或是y>0，平行于x轴，或是y<0，平行于x轴？
解决了这个问题，整个问题就解决了。

2019年8月14日 23:12:32

已经修改了原来错误的main方法。不能简单使用x<0,x>0,y<0,y>0进行判断，应该将点精确到
left，up，right，down所在范围的线段上。

2019年8月14日 23:17:39

新增了（-6，-1）=125，（2，8）=250两组测试数据

附：另一位博主解法，可供本文算法结果校验。
https://blog.csdn.net/Heloiseeeeeee/article/details/87987709

2019年8月14日 23:26:05

添加了程序运行时间统计，单位为纳秒。ps：1ms=1000000ns，时间太短，ms统计已经为0.
测试了几组大数。结果如下：

PS：10亿时，性能还是很好。

由于本人水平有限，如有错误之处，欢迎指出。