matlab练习程序（最大流/最小割）

学习这个算法是为学习图像处理中的图割算法做准备的。

基本概念：

1.最大流是一个有向图。

2.一个流是最大流，当且仅当它的残余网络中不包括增广路径。

3.最小割就是网络中所有割中值最小的那个割，最小割是不唯一的，不过最小割的值是唯一的。

4.最大流的流量等于某一最小割的容量。

算法思想就是Ford-Fulkerson方法。

具体流程：

1.首先使用广度优先搜索找到源节点到汇节点的一条路径，为增广路径。

2.如果找不到新的从源到汇的增广路径，则上一次求得的网络就是最大流，否则向下执行。

3.找出增广路径中最小的路径的值。

5.用路径中最小的值构造最大流网络，原网络包含这个网络。

4.将增广路径中所有的路径减去最小路径这个值，形成新的网络图。

6.对新的网络图继续执行第1步。

网络图如下，没什么好办法形象表示。我比较懒，不想画图了，真想看明白过程就看算法导论405页。

原网络：

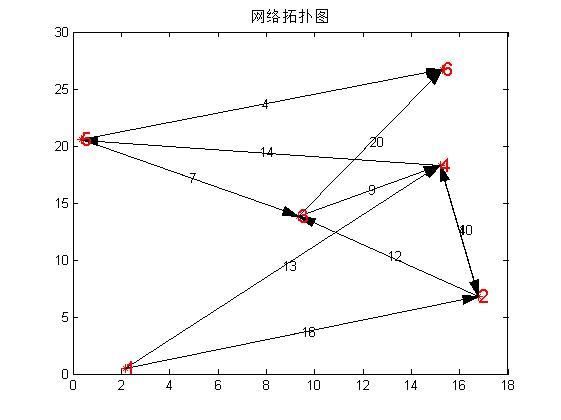
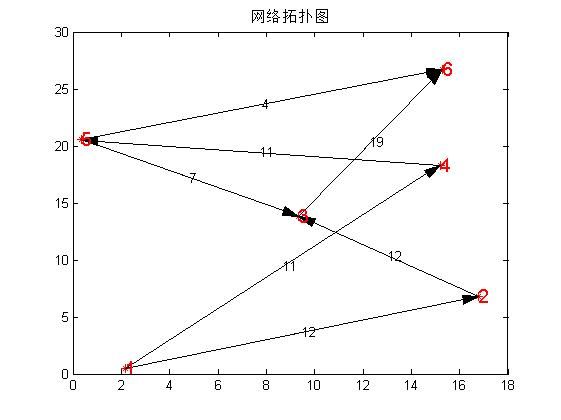
最大流：

matlab代码如下：

clear all;close all;clc

%初始化邻接压缩表，算法导论405页的图



b=[1 2 16;

   1 4 13; 

   2 3 12;

   2 4 10;

   3 4 9;

   3 6 20;

   4 2 4;

   4 5 14;

   5 3 7;

   5 6 4];



m=max(max(b(:,1:2)));       %压缩表中最大值就是邻接矩阵的宽与高

A=compresstable2matrix(b);  %从邻接压缩表构造图的矩阵表示

netplot(A,1);



maxflow=zeros(m,m);

while 1              %下面用广度优先搜索找增广路径

    flag=[];            %相当于closed表，已访问过的节点

    flag=[flag 1];   

    head=1;

    tail=1;

    queue=[];           %队列，相当于open表，将要访问的节点

    queue(head)=1;

    head=head+1;



    pa=zeros(1,m);      %每个节点的前趋

    pa(1)=1;            %源节点前趋是自己

    while tail~=head    %广度优先搜索，具体细节就不注释了

        i=queue(tail);

        for j=1:m

            if A(i,j)>0 && isempty(find(flag==j,1))

                queue(head)=j;

                head=head+1;

                flag=[flag j];

                pa(j)=i;

            end

        end

        tail=tail+1;

    end



    if pa(m)==0     %如果搜索不到汇节点，退出循环

        break;

    end

    

    path=[];

    i=m;                %从汇节点开始

    k=0;                %路径包含的边的个数

    while i~=1          %使用前趋构造从源节点到汇节点的路径

        path=[path;pa(i) i A(pa(i),i)];     %存入路径

        i=pa(i);            %使用前趋表反向搜寻，借鉴Dijsktra中的松弛方法

        k=k+1;             

    end

    Mi=min(path(:,3));        %寻找增广路径中最小的那条边

    for i=1:k  

        A(path(i,1),path(i,2))=A(path(i,1),path(i,2))-Mi;     %增广路径中每条路径减去最小的边  

        maxflow(path(i,1),path(i,2))=maxflow(path(i,1),path(i,2))+Mi;   %最大流，原网络包含这个网络，我只能这样表示了

    end                     %使用新的图A进入下一循环，从新开始找增广路径

end    



figure;

netplot(maxflow,1)

这里没有连通的路径值为0.