数据结构与算法（一）：算法基础及递归典型问题（Python实现)

概念
算法概念
时间复杂度
空间复杂度
递归问题
斐波那契数列
汉诺塔问题

---

一、 概念

1、算法的概念
一个计算过程，解决问题的方法。规定的输入得到规定的输出。
2、时间复杂度
O(1)：时间复杂度最小单位（加法、减法、打印等）

print('hello world')`

O(n)

for i in range(n):
	print('hello world')

O($n^2$)

for i in range(n):
	for j in range(n):
		print('hello world')

O($n^3$)

for i in range(n):
	for j in range(n):
		for k in range(n):
			print('hello world')

其中：n 为问题规模，n的数值足够大。
O(1)

print('Hello World')
print( 'Hello Python')
print('Hello Algorithm')

O($n^2$)

for i in range(n):
	print('Hello World')
	for j in range(n):
		print('Hello World')

O($n^2$)

for i in range(n):
	for j in range(i):
		print('Hello World')

O(${\log }_2^n$)=O(logn)

while n>1:
	print(n)
	n = n // 2

O(1) < O(${\log }_2^n$) < O($n^2$)
如果可以将O($n^2$)简化成O(${\log }_2^n$)，就认为算法很高效。
总结：
时间复杂度是用来估计算法运行时间的一个式子(单位)。
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度(按效率排序)：
O(1) < O(logn) < O(n) < O(nlogn) < O($n^2$) < O($n^2$logn) < O($n^3$)
3、空间复杂度
概念：用来评估算法内存占用大小的式子
表示：O(1),O(n) / S(1),S(n) / T(1),T(n)
大概描述：
O(1) : 几个临时变量
O(n) : 开辟长度为n的列表
O($n^2$) : 开辟长度为n的二维列表
为了效率，通常“空间换时间”，所以对空间复杂度讨论的不多。

二、递归问题

递归的两个特点：

• 调用自身
• 结束条件

def func3(x):
	if x > 0:
		print(x)
		func3(x-1)

---

1、斐波那契数列题目解法及优化

斐波那契数列 1 1 2 3 5 8 …
F(n) = F(n-1) + F(n-2) F(0)=1 F(1)=1

解法1：

# 斐波那契数列 1 1 2 3 5 8 ...
# F(n) = F(n-1) + F(n-2)   F(0)=1  F(1)=1
def fibnacci(n);
	if n == 0 or n==1:
		return 1
	else:
		return fibnacci(n-1) + fibnacci(n-2)
print(fibnacci(4))

上述代码存在的问题：递归写出来的代码时间复杂度极高。
好奇的话可以测试一下时间复杂度：
（递归函数调时间会出问题所以套个马甲（fib1函数））

# 斐波那契数列 1 1 2 3 5 8 ...
# F(n) = F(n-1) + F(n-2)   F(0)=1  F(1)=1
import time
def fibnacci(n);
	if n == 0 or n==1:
		return 1
	else:
		return fibnacci(n-1) + fibnacci(n-2)
print(fibnacci(4))

@cal_time
def fib1(n):
	return fibnacci(n)
print(fib1(30))

可以运行计算感受一下，每增1运行时间会成倍增长。递归算法本身就很慢。
且重复计算问题，导致时间复杂度极高。
为避免重复计算，可以优化算法结构，将重复计算值存起来。
解法2：
优化fib1函数：

def fib2(n):
	li = [1,1]
	for i in range(2, n+1):
		li.append(li[-1]+li[-2])
	return li[n]

时间复杂度：O(n)
空间复杂度：O(n)（列表空间造成了浪费）
上述代码存在的问题：虽然时间复杂度减少了，但在空间上造成了浪费。
优化列表长度，不需要将所有数据全部存入列表，实际上只需要存两个计算项，一个输出项，列表长度为3即可。
解法3：
优化fib2函数：

def fib3(n):
	a=1
	b=1
	c=1
	for i in range(2, n+1):
		c = a + b 
		a = b
		b = c
	return c

时间复杂度：O(n)
空间复杂度：O(1)
解法4：
运用斐波拉契通项公式

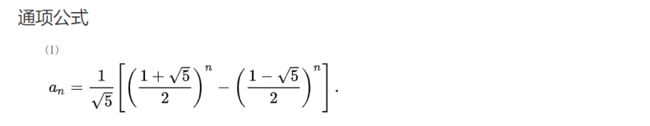
上述解法存在问题：由于计算机计算$\sqrt{5}$数值不精确，当n特别大的时候数会飘，会产生错误。尽量不使用该解法。

---

斐波拉契数列相关题型
一段有n个台阶组成的楼梯，小明从楼梯的最底层向最高处前进，它可以选择一次迈一级台阶或者一次迈两级台阶。问他有多少种不同的走法?

分析：
一级台阶：1种走法
两级台阶：2种走法
三级台阶：3种走法
四级台阶：5种走法
五级台阶：8种走法
六级台阶：13种走法
…
可以找出规律，前面加个1，就是斐波拉契数列。

思路：
① 假设n个台阶，第一步先走一级台阶，剩下n-1阶台阶，即F(n-1)有多少走法，即为题解。
② 假设n个台阶，第一步先走两级台阶，剩下n-2阶台阶，即F(n-2)有多少走法，即为题解。
递归式子：F(n) = F(n-1) + F(n-2)
终止条件：
一级台阶走法F(1) = 1
两级台阶走法F(2) = 2
即最终将该问题抽象成2个斐波那契数列问题，上文已给出4种解法。

其他类型问题：
① 1x1，1x2瓷砖铺法问题（与上题一样）
② 上述台阶问题修改为可以一次走3个台阶，问走法。（不再是斐波那契数列，但递归式子可以写出来，可以采用上文的列表存储或者使用4个变量进行计算，初始值也需要计算3个）

---

2、汉诺塔问题
大梵天创造世界的时候做了三根金刚石柱子，在一根柱子，上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
64根柱子移动完毕之日，就是世界毁灭之时。
思路：
n个盘子时：

1. 把n-1个圆盘从A经过C移动到B
2. 把第n个圆盘从A移动到C
3. 把n-1个小圆盘从B经过A移动到C

递归：大问题和小问题本身是一个问题，解决大问题拆成小问题解决。实际上的大问题都是由小问题构成的。降低了问题的规模。
解法：

def hanoi(n, A, B, C)
	if n > 0:
		hanoi(n-1, A, C, B)  # A经过C移到B
		print('%s -> %s'% (A,C)) #固定的一步，打印
		hanoi(n-1, B, A, C) # B经过A移到C
hanoi(64, 'A', 'B', 'C')

验证3个盘时输出结果：
A->C
A->B
C->B

A->C

B->A
B->C
A->C
通过移动发现，n=3（3个盘）一共7步，前三步和后三步是2个 n=2（2个盘）的移动。
若n=2（2个盘） 是一共三步，前后拆开是两个 n=1 的移动。

---

汉诺塔移动次数的递推式: h(n)=2h(n-1)+1
h(64)= 18446744073709551615
假设婆罗每秒钟搬一个盘子，则总共需要5800亿年!