java集合之TreeMap源码分析
java集合(6):TreeMap源码分析(jdk1.8)
重点:红黑树(一)之 原理和算法详细介绍
TreeMap的基本概念:
TreeMap集合是基于红黑树(Red-Black tree)的 NavigableMap实现。该集合最重要的特点就是可排序,该映射根据其键的自然顺序进行排序,或者根据创建映射时提供的 Comparator 进行排序,具体取决于使用的构造方法。这句话是什么意思呢?就是说TreeMap可以对添加进来的元素进行排序,可以按照默认的排序方式,也可以自己指定排序方式。
根据上一条,我们要想使用TreeMap存储并排序我们自定义的类(如User类),那么必须自己定义比较机制:一种方式是User类去实现java.lang.Comparable接口,并实现其compareTo()方法。另一种方式是写一个类(如MyCompatator)去实现java.util.Comparator接口,并实现compare()方法,然后将MyCompatator类实例对象作为TreeMap的构造方法参数进行传参(当然也可以使用匿名内部类),这些比较方法是怎么被调用的将在源码中讲解。
下图是Map集合体系类图。
![]()
前提:阅读本文最好对红黑树有基本的了解
介绍
- 扩展AbstractMap类并实现NavigatebleMap接口
- 访问和检索时间相当短,这使得TreeMap成为存储需要快速找到的大量排序信息的绝佳选择
- 树实现
- 适用于按自然顺序或自定义顺序遍历键(key)
- 不允许键为Null
- 非线程安全
- 具有fail-fast机制
继承关系 继承类介绍
AbstractMap:继承AbstractMap,它实现了Map接口,提供了Map接口的基本实现
NavigableMap:该接口继承自SortedMap接口,它的所有方法都是为定位设计的
变量解析(所有代码都不是完整的源码,而是精简过后的源码!结合源码食用更佳)
//比较器 用于维护映射的顺序 为null键使用自然排序
private final Comparator comparator;
//红黑树根节点
private transient Entry root;
//数据实际数量
private transient int size = 0;
//结构被修改次数
private transient int modCount = 0; 红黑树数据结构
static final class Entry implements Map.Entry {
K key;
V value;
//左节点
Entry left;
//右节点
Entry right;
//父节点
Entry parent;
//节点颜色 root节点为黑色
boolean color = BLACK;
Entry(K key, V value, Entry parent) {...}
public K getKey() { return key;}
public V getValue() {return value;}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
} put(K key, V value):
将指定值与该映射中的指定键相关联。如果该映射先前包含该键的映射,则将替换旧值。没有映射或value为空都返回null(但是会添加该映射,只是必须返回旧值才不得不这样做,返回null不代表put失败).该方法允许空值,Key是否可以为空要看具体情况,null Key可能会抛异常也可能不会(取决于你有没有自己实现Comparator, 没有实现的话就要抛空指针异常,因为不能在null对象上使用compareTo())
public V put(K key, V value) {
Entry t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check,不理解为啥要类型检查
//构建根节点
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
//按比较器和可比较的路径分类
Comparator cpr = comparator;
if (cpr != null) {
//从根节点一直搜索到key值相同的节点或者null(找不到相同的就添加)
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
//不允许null键存在
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key; //利用key自带的比较器
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//处理未找到相同键的情况:生成节点
Entry e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//维护此树的特性(修改节点颜色或左旋右旋等操作)以保证其成为红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
} 使用put(k,v)在树的末尾添加了叶子节点(将其颜色默认设置为红色)后,需要进行“双红修正”(假设其父节点为红色),即fixAfterInsertion(Entry x)
/** From CLR */
private void fixAfterInsertion(Entry x) {
//将节点染成红色,再做双红修正
x.color = RED;
//x不能是root,因为root节点parent为null;x的父节点也必须为红,否则没必要修正
while (x != null && x != root && x.parent.color == RED) {
//在x,x.parent,x.parent.parent中有四种结构(左孩子or右孩子),且要关注x的叔父节点(即x的父节点的兄弟节点是否为红)
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
//此时x,x.parent,x.parent.parent,x.parent.parent.right在一个超级节点中,发生上溢
//将祖父节点提升至上层超级节点(即染红)并将祖父节点所有孩子染黑,此时上层超级节点也有可能发生上溢,所以将x = parentOf(parentOf(x))继续检查直至根节点(O(logN))
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
//叔父节点是黑,则需要作一次"3+4"重构(根据x与x.parent的位置旋转1-2次),并将中间染黑,两边染红
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x); //zag-zig
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
//与上面同理
Entry y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
//转换为zag-zag标准情况
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK; //不要忘记root节点规定必须为黑色
} 下面看一下左旋rotateLeft(Entry
/** From CLR */
private void rotateLeft(Entry p) {
//左旋分两种情况:p是左孩子还是右孩子
if (p != null) {
Entry r = p.right;
p.right = r.left; //r的左孩子作了p的右孩子
if (r.left != null)
r.left.parent = p; //换p的右孩子的父节点
r.parent = p.parent;
if (p.parent == null)
root = r; //换r的父节点(若p就是根,还要给root赋值为r)
else if (p.parent.left == p)
p.parent.left = r; //区别p的左孩子还是右孩子
else
p.parent.right = r;
r.left = p;
p.parent = r; //r与p建立父子关系
}
}
/** From CLR */
private void rotateRight(Entry p) {
右旋分两种情况:p是左孩子还是右孩子
if (p != null) {
Entry l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
} getEntry:一帮以getEntry()方法为基础的获取元素的方法,其中包括containsKey(),get(),remove()等。get()返回Map中与key相关的值,或当key不存在时返回null。如果在Map中不存在null值,那么由get返回的值可以用来确定key是否在Map中。然而如果存在null值,那么必须使用containsKey()
//返回指定的Entry或者null
final Entry getEntry(Object key) {
// Offload comparator-based version for sake of performance
//根据指定的比较器查找
if (comparator != null)
return getEntryUsingComparator(key);
//不允许null键
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
//从根节点开始查找
Entry p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
//使用比较器的getEntry版本。从getEntry中分离出来。(对于不太依赖比较器性能的大多数方法来说,这不值得这样做,但是在这里值得这样做)
final Entry getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator cpr = comparator;
if (cpr != null) {
Entry p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
} remove(Object key)
作用:如果存在,则从thisTreeMap中删除此键对应的Entry并返回value
public V remove(Object key) {
Entry p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
} deleteEntry(Entry p)
将红黑树内的某一个节点删除。需要执行的操作依次是:首先,将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除;然后,通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。详细描述如下:
第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
private void deleteEntry(Entry p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// 空出链接,以便fixAfterDeletion可以使用它们
p.left = p.right = p.parent = null;
// 被删除节点与它的替代节点有两种情况:1)其中一个为红色,一个为黑色,此时将替代节点染黑就行 2)都是黑色的,则须双黑修正四种情况
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. 使用self作为幻像替换并取消链接
if (p.color == BLACK)
fixAfterDeletion(p); //由于在红黑树定义中,空节点用黑色的叶子节点来定义,所以此时也属于“双黑修正”
//清楚p节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
} 删除节点后需要作"双黑修正"
下面对删除函数进行分析。在分析之前,我们再次温习一下红黑树的几个特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
前面我们将"删除红黑树中的节点"大致分为两步,在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"特性(2)、(4)、(5)"三个特性。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
为了便于分析,我们假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。为什么呢?
通过RB-DELETE算法,我们知道:删除节点y之后,x占据了原来节点y的位置。 既然删除y(y是黑色),意味着减少一个黑色节点;那么,再在该位置上增加一个黑色即可。这样,当我们假设"x包含一个额外的黑色",就正好弥补了"删除y所丢失的黑色节点",也就不会违反"特性(5)"。 因此,假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。
现在,x不仅包含它原本的颜色属性,x还包含一个额外的黑色。即x的颜色属性是"红+黑"或"黑+黑",它违反了"特性(1)"。
现在,我们面临的问题,由解决"违反了特性(2)、(4)、(5)三个特性"转换成了"解决违反特性(1)、(2)、(4)三个特性"。RB-DELETE-FIXUP需要做的就是通过算法恢复红黑树的特性(1)、(2)、(4)。RB-DELETE-FIXUP的思想是:将x所包含的额外的黑色不断沿树上移(向根方向移动),直到出现下面的姿态:
a) x指向一个"红+黑"节点。此时,将x设为一个"黑"节点即可。
b) x指向根。此时,将x设为一个"黑"节点即可。
c) 非前面两种姿态。
将上面的姿态,可以概括为3种情况。
① 情况说明:x是“红+黑”节点。
处理方法:直接把x设为黑色,结束。此时红黑树性质全部恢复。
② 情况说明:x是“黑+黑”节点,且x是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。
③ 情况说明:x是“黑+黑”节点,且x不是根。
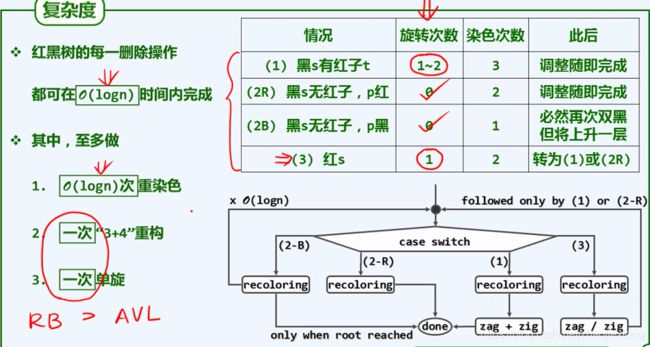
处理方法:这种情况又可以划分为4种子情况。这4种子情况如下表所示:
| 现象说明 | 处理策略 | |
| Case 1 | x是"黑+黑"节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。情况为BB-3:一次zig或zag旋转。虽然黑高度的异常虽然存在,但已经转换为BB-1或BB-2R(绝不是BB-2B),这样再经一轮调整之后,红黑树的性质必全局恢复 | (01) 将x的兄弟节点设为“黑色”。 |
| Case 2 | x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。如果x的父节点是红色,则为BB-2R,只需两次染色(父节点染黑,兄弟节点染红)即可完成;如果x的父节点是黑色,则为BB-2B,则必须将x的兄弟节点染红,且设置“x的父节点”为“新的x节点”。 | (01) 将x的兄弟节点设为“红色”。 |
| Case 3 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。BB-1,一次旋转,三次染色 | (01) 将x兄弟节点的左孩子设为“黑色”。 |
| Case 4 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。BB-1,两次旋转,三次染色 | (01) 将x父节点颜色 赋值给 x的兄弟节点。 |
/** From CLR */
//被删除节点与它的替代节点有两种情况:1)其中一个为红色,一个为黑色,此时将替代节点染黑就行 2)都是黑色的,则须双黑修正四种情况
private void fixAfterDeletion(Entry x) {
//deleteEntry中传入了替代节点replacement,但此时该节点已经替代了被删除节点的位置
while (x != root && colorOf(x) == BLACK) {
//用if-else分x为左右孩子两种情况
if (x == leftOf(parentOf(x))) {
Entry sib = rightOf(parentOf(x)); //x的兄弟节点,也可能不存在
//对应于BB-3
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x)); //此时兄弟节点变为x的父节点的右孩子,退化为BB-1或BB-2R
}
//兄弟节点为黑色节点,父节点为红色节点,则根据兄弟节点是否有红孩子分为BB-1(至少一个红孩子)和BB-2R(都是黑孩子)
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x); //退出循环,X父节点染黑
} else {
if (colorOf(rightOf(sib)) == BLACK) { //左孩子红,右孩子黑,则左孩子染黑,右旋sib并染红sib
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x)); //左孩子左旋后链接到x的父节点
}
//转换为标准的右孩子为红之后,就可以作“3+4”重构
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root; //退出循环,并将x(即root)染黑
}
} else { // 同理
Entry sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
} replace(K key, V value)
作用:替换指定键映射的值
public V replace(K key, V value) {
Entry p = getEntry(key);
if (p!=null) {
V oldValue = p.value;
p.value = value;
return oldValue;
}
return null;
} get(Object key)
作用:返回指定键映射到的值
返回值{@code null}不一定表示该映射不包含该键的映射。 映射也可能将键显式映射到{@code null}。 {@link #containsKey containsKey}操作可用于区分这两种情况。
public V get(Object key) {
Entry p = getEntry(key);
return (p==null ? null : p.value);
} public boolean containsKey(Object key) {
return getEntry(key) != null;
}