HDU 3567 Eight II (BFS+映射+康托展开)
题面
Eight-puzzle, which is also called "Nine grids", comes from an old game.
In this game, you are given a 3 by 3 board and 8 tiles. The tiles are numbered from 1 to 8 and each covers a grid. As you see, there is a blank grid which can be represented as an 'X'. Tiles in grids having a common edge with the blank grid can be moved into that blank grid. This operation leads to an exchange of 'X' with one tile.
We use the symbol 'r' to represent exchanging 'X' with the tile on its right side, and 'l' for the left side, 'u' for the one above it, 'd' for the one below it.
A state of the board can be represented by a string S using the rule showed below.
The problem is to operate an operation list of 'r', 'u', 'l', 'd' to turn the state of the board from state A to state B. You are required to find the result which meets the following constrains:
1. It is of minimum length among all possible solutions.
2. It is the lexicographically smallest one of all solutions of minimum length.
Input
The first line is T (T <= 200), which means the number of test cases of this problem.
The input of each test case consists of two lines with state A occupying the first line and state B on the second line.
It is guaranteed that there is an available solution from state A to B.
Output
For each test case two lines are expected.
The first line is in the format of "Case x: d", in which x is the case number counted from one, d is the minimum length of operation list you need to turn A to B.
S is the operation list meeting the constraints and it should be showed on the second line.
Sample Input
2
12X453786
12345678X
564178X23
7568X4123Sample Output
Case 1: 2
dd
Case 2: 8
urrulldr题目链接
HDU_3567_Eight II
参考链接
简单版:HDU_1043_Eight(建议先做八数码问题的简单版本:HDU1043)
简单版题解:HDU 1043 Eight (八数码问题 康托展开 bfs)
题解参考:Eight II HDU - 3567 (bfs打表+hash映射+康托展开)author :一只二十四节气
映射理解示意图:hdu 3567 author:wang_viscaria
数据生成代码(含样例):hdu 3567 Eight II 八数码 双向BFS author : knownothing
题目简述
比HDU1043 Eight复杂一些的八数码问题,要求从给定的起始状态ori_start,到目标状态ori_target
最多有200组数据。
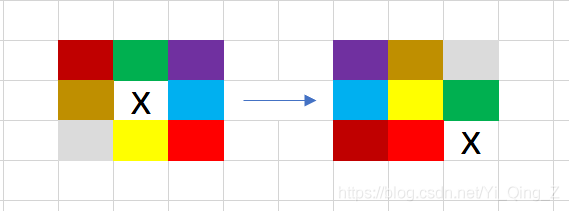
把数字的移动理解成位置的移动。
如下图:数字的移动实际上颜色块的移动,即使颜色上填的数字不同,也不会影响答案序列。
由数字得到颜色,继而得到答案,根据X所在的位置分类,一共有9种情况。
(用9代替‘X’)
912345678
192345678
129345678
123945678
123495678
123459678
123456978
123456798
123456789
以这九种状态作为起点进行正向BFS搜索打表。
处理每组样例时,根据起始状态制定映射规则,把起始状态和终止状态进行转化。从终止状态target回溯到起始状态start,由表获得答案序列,逆序输出结果。
不能根据终止ori_target状态,制定映射规则,这样不能保证字典序最小lexicographically smallest,亲身试验深有体会。因为以上述九种状态作为BFS搜索树的根节点时,假如,由终点->起点先有路径“druu”(倒过来“uurd”),那么当有更优解“urdd”(倒过来“ddru”)时,则不会填入表中。无法保证字典序最小,所以此题与HDU1043不同。此题采用的是正向bfs打表。而HDU1043采用的是反向bfs打表。
bfs的顺序必须按照“dlru”,来保证字典序最小。
程序分析
int factorial[10];/**保存阶乘的数组**/
int dire_x[]={1,0,0,-1};/**方向数组**/
int dire_y[]={0,-1,1,0};/**方向**/
char w[]="dlru";/**方向对应数组**/
char contact[10];/**记录映射规则的数组**/
char MAP[10][10];/**存放初始9种状态**/
char answer[50];/**答案数组**/
struct Node/**BFS搜索树的结点**/
{
char way;
int father;
}node[10][370000];/**987654321的康托展开值为362879,即由1-9组成的序列的最大康托展开值为362879**/
struct Path/**状态**/
{
char a[10];
int where/**x在a中的位置**/,Can_num/**康托展开值**/;
}ori_start,start,ori_target,target;/**起始状态和映射后的状态**/
void init()/**初始化数组**/
void set_factorial()/**计算阶乘**/
int cantor(char can[])/**康托展开**/
void copy_Path(Path &x,Path y)/**深拷贝**/
void bfs(char xx[],int num)/**bfs正向搜索**/
void tanslation()/**制定映射规则,得到映射后的start,target**/
程序
#include
#include
#include
#include
using namespace std;
int factorial[10];
int dire_x[]={1,0,0,-1};
int dire_y[]={0,-1,1,0};
char w[]="dlru";
char contact[10];
char MAP[10][10];
char answer[50];
struct Node
{
char way;
int father;
}node[10][370000];
struct Path
{
char a[10];
int where/**x在a中的位置**/,Can_num;
}ori_start,start,ori_target,target;
void init()
{
for(int i=0;i<9;i++)
{
int j=1;
for(int k=0;k<9;k++)
{
if(k==i)
MAP[i][k]='9';
else
MAP[i][k]='0'+j++;
}
}
for(int i=0;i<370000;i++)
for(int j=0;j<9;j++)
node[j][i].father=-1;
}
void set_factorial()/**计算阶乘**/
{
factorial[0]=1;
for(int i=1;i<=8;i++)
{
factorial[i]=factorial[i-1]*i;
}
}
int cantor(char can[])/**康托展开**/
{
int ans=0,k;
for(int i=0;i<9;i++)
{
k=0;
for(int j=i+1;j<9;j++)
if(can[j]Q;
Path p,q;
for(int i=0;i<9;i++)
q.a[i]=xx[i];
q.where=num;
q.Can_num=cantor(q.a);
node[num][q.Can_num].father=-2;
Q.push(q);
while(!Q.empty())
{
copy_Path(q,Q.front());
Q.pop();
for(int i=0;i<4;i++)
{
copy_Path(p,q);
int x=q.where/3+dire_x[i];
int y=q.where%3+dire_y[i];
if(x>=0&&x<3&&y>=0&&y<3)
{
p.where=x*3+y;
char temp=p.a[p.where];
p.a[p.where]=p.a[q.where];
p.a[q.where]=temp;
p.Can_num=cantor(p.a);
if(node[num][p.Can_num].father==-1)
{
node[num][p.Can_num].father=q.Can_num;
node[num][p.Can_num].way=w[i];
Q.push(p);
}
}
}
}
}
void tanslation()
{
for(int i=0;i<9;i++)
{
if(ori_target.a[i]=='X')
{
ori_target.where=i;
ori_target.a[i]='9';
}
if(ori_start.a[i]=='X')
{
ori_start.a[i]='9';
ori_start.where=i;
}
}
for(int i=0;i<9;i++)
{
contact[ori_start.a[i]-'0']=MAP[ori_start.where][i];
}
for(int i=0;i<9;i++)
{
start.a[i]=contact[ori_start.a[i]-'0'];
target.a[i]=contact[ori_target.a[i]-'0'];
}
start.Can_num=cantor(start.a);
target.Can_num=cantor(target.a);
start.where=ori_start.where;
target.where=ori_target.where;
}
int main()
{
init();
set_factorial();
for(int i=0;i<9;i++)
bfs(MAP[i],i);
int T;
scanf("%d",&T);
for(int e=1;e<=T;e++)
{
scanf("%s",ori_start.a);
scanf("%s",ori_target.a);
tanslation();
int cant=target.Can_num;
memset(answer,'\0',sizeof(answer));
int step=0;
while(cant!=-2)
{
answer[step++]=node[ori_start.where][cant].way;
cant=node[ori_start.where][cant].father;
}
step=strlen(answer);
printf("Case %d: %d\n",e,step);
for(int i=step;i>=1;i--)
printf("%c",answer[i-1]);
printf("\n");
}
return 0;
}