机器学习-社区发现算法介绍（一）：Infomap

在诸多互联网金融风控的场景里，团伙识别是相当重要的一项工作。如果恶意攻击者以团伙的方式尝试获取利益，比如骗贷、骗保、薅羊毛，通常都会给对应的公司带来不小的经济损失。团伙识别有各种各样的方法，其中最主要的方法就是“社区发现”（community detection）类算法，常规的方法有 Louvain，Label Propagation，Infomap 等等。

算法核心思想

社区发现类算法似乎并不存在一个最好的算法，因为在现实数据中对于社区或者说团伙的定义千差万别，不一定都跟算法的假设匹配。有一些学术文章尝试过对于最近十几年提出的算法进行比较，发现在一些常规评价指标（比如，modularity）上表现比较好的算法，可能在有 ground truth 的真实数据上表现不太好；在其中一些真实数据上表现好的算法，可能在另一些真实数据上表现并不好。在现实应用中，最为保险的做法，可能是尽量了解一些不同思路的算法，以备不时之需。而 Infomap 是众多社区发现算法中思路比较特别的一种算法。

 

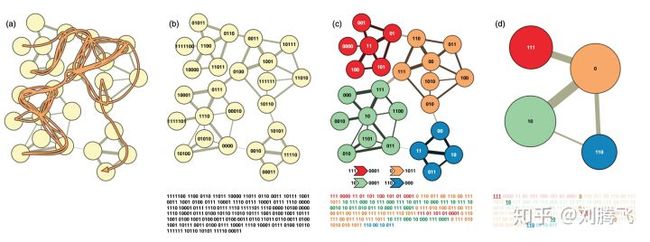
Infomap 设计之初想解决的问题如下：如果在一张图上做随机游走（不限步数的游走），如何用最短的编码来描述随机游走产生的路径？比如，下图（a）中展示了一段随机游走产生的路径，那怎么描述它先访问了哪个节点，后访问了哪个节点呢？

 

原始做法： 采用等长的二进制编码，每个节点一个编码，不同节点之间的编码不一样。

 

高级做法：采用 huffman 编码，每个节点一个编码，但是码的长度不一样。对于访问频率比较高的给予较短的编码，对于访问频率比较低的给予较长的编码。下图（b）展示了这样的编码，显然，相比较等长编码，采用huffman编码可以缩短描述的信息长度。

 

进阶做法：采用双层结构，将不同节点划分群组（这里的“群组”同“社区”是等价的概念），这样在编码时候需要对两种信息编码。第一种是群组的名字，不同群组的名字编码不一样；第二种是每个群组内部的节点，不同节点的名字编码不一样。但是，不同群组内部的节点的编码可以复用。显然，在划分群组之后，每个群组内部节点相对较少，可以采用短一些的编码。不同群组内部节点的编码复用，可以大幅缩短描述的信息长度。

 

不同群组内部节点的编码复用，就好比不同城市里街道的名字可以相同一样，上海有南京路，武汉有南京路，青岛也可以有南京路。

 

Infomap 在具体做法上，为了区分随机游走从一个群组进入到了另一个群组，除了群组的名字之外，对于每个群组的跳出动作也给予了一个编码。比如，下图（c）中红色节点部分是一个群组，群组名的编码是 111，跳出编码是 0001。这样在描述某个群组内部的一段随机游走路径的时候，总是以群组名的编码开头，以跳出编码结束。

 

算法步骤简述

Infomap 的双层编码方式把群组识别（社区发现）同信息编码联系到了一起。一个好的群组划分，可以带来更短的编码。所以，如果能量化编码长度，找到使得长度最短的群组划分，那就找到了一个好的群组划分。

 

那如何量化编码的长度呢？假设现在有一种群组划分方式 M 将节点划分为 m 个群组, 则描述随机游走的平均每步编码长度（average number of bits per step）可以用下面这个公式来度量：

 

 

在上面的公式里用到的最重要的概念是信息熵 H(X)。熵在一般的理解里是用来描述“系统混乱程度”的，当一个随机变量为均匀分布的时候，它的状态最不确定，系统最混乱不可预测，这个时候熵最大。 而在编码理论里，熵还有一个解释是 “编码每个状态所需的平均字节长度”。阮一峰有一篇通俗易懂的文章是解释信息熵的：《数据压缩与信息熵》，有兴趣的可以一读。

 

上面的公式里, 有四个变量，其含义分别为：

• : 在编码中所有表示群组名字的编码的占比， 表示群组 i 的名字出现的概率（或者，也等于从群组 i 跳出的概率）

 

• : 编码群组名字所需的平均字节长度

 

• ：在编码中属于群组 i 的所有节点（包括跳出节点）的编码的占比

 

• ：编码群组 i 中所有节点所需的平均字节长度（注意：跳出编码也作为一个虚拟节点放在了各自群组内一起编码）

 

简单的理解上面这个公式：平均每步编码长度 是两部分的加权和，一个是编码群组名字所需的平均字节长度，一个是编码每个群组中的节点所需的平均字节长度，权值是各自的占比。

 

如果要计算上述四个变量的值，我们只需要知道图中每个节点的访问概率和每个群组的跳转概率。其中访问概率的计算方法，Infomap 采取了类似 pagerank 的做法：

 (1) 初始所有节点都是均匀访问概率；
 (2) 在每个迭代步骤里，对于每个节点  有两种方式跳转：要么以 1-r 的概率从节点 a 的连接边中选择
   一条边进行跳转，选每条边的概率正比于边的权重；要么以 r 的概率从节点 a 随机的跳到图上其他任意
   一点。
 (3) 重复步骤 2 直到收敛。

 

当访问概率收敛之后，即得到图中每个节点的访问概率，这样每个群组的跳转概率也可以计算了，更进一步的 也就可以计算了。 如下所示，这里的 是归一化的从节点 跳转到节点 的权重，群组 i 的跳转概率为：

 

 

总结一下，Infomap 算法的大体步骤如下（看起来跟 Louvain 有些许类似）：

（1）初始化，对每个节点都视作独立的群组；
（2）对图里的节点随机采样出一个序列，按顺序依次尝试将每个节点赋给邻居节点所在的社区，取平均比特
    下降最大时的社区赋给该节点，如果没有下降，该节点的社区不变；
（3）重复直到步骤 2 直到 L（M）不再能被优化。

参考文献

1. The map equation：http://www.mapequation.org/assets/publications/EurPhysJ2010Rosvall.pdf
2. Maps of random walks on complex networks reveal community structure：http://www.mapequation.org/assets/publications/RosvallBergstromPNAS2008Full.pdf