动态规划之斜率优化

其实斜率优化也是用的单调队列来的。
一般的例如： dp[ i ]=min( dp[ j ] + f（j）) ( i-k< j < i ) 我们可以用单调队列来优化，因为变量只有j。 而如dp[ i ]=min(dp[ j ]+ f ( i ) * f ( j ) )的话,i和j在一起的了，就不能单调队列优化了。
先上一道斜率优化模板题https://www.luogu.com.cn/problem/P3195
从题目我们可以得知是dp题，并且方程如下：
dp[i]=min(dp[j]+((sum[i]-sum[j])+(i-(j+1))-L)^2);
dp[i]表示前i个所需的费用，sum[i]表示前i个的前缀和。
令sum[i]+i=f(i) ,sum[j]+j+L+1=f(j)
dp[i]=dp[j]+(f(i)-f(j))^2;
dp[j]+f(j)^2 = 2f(i)f(j) + dp[i]- f(i)^2;
因为我们枚举的是j，所以j是变量，而i是知道的，所以我们令dp[j]+f(j)^2 =y,f(j)=x,2f(i)=k,dp[i]-f(i)^2=b;
上面就可以变为y=kx+b；其实求的dp[i]就是求的截距，而我们要求的最小值，就是截距最小。
我们要的是前面的某个值最小，所以我们设k dp[j]+f(i)^2 -2f(i)f(j)+ f(j)^2< =dp[k]+f(i)^2- 2f(i)f(k)+f(k)^2
dp[j]+f(j)^2 -dp[k]-f(k)^2 <=2f(i) * (f(j)-f(k))
dp[j]+f(j)^2 -dp[k]-f(k)^2/(f(j)-f(k))<=2*f(i)
所以我们令dp[i]+f(i)^2=Y(i)，所以斜率Y(j)-Y(k) / ( f (j) - f (k) ) <= 2f(i)
因此如果j>k，并且斜率满足上面的不等式的话，那么j就比k优。
然后接下来要怎样呢，单调队列要何用。
我们假设k
有三种情况：
slope(i,j)f(i)的话，i比j优，j比k优,所以j不是最优的
slope(i,j)<2f(i)f（i）了，所以和之前矛盾，变成k比j优）,j不是最优的
2*f(i) 所以无论是哪种情况，j都不是最优的。
也就是说通过这种的话，我们无法去这个区间里找到最优的解。
因此要slope(i,j)>slope(j,k)，如下图所示

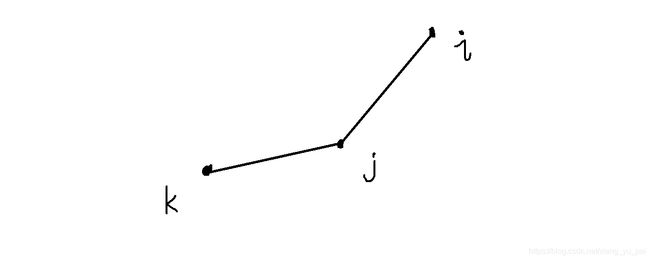
其实我们上面说了求截距最小值嘛，所以像上面这图一样（下凸包），在j点才能取得最小值，我们可以想象一下k=2*f(i) （k>0）的直线从最下面开始往上升，最先碰到的就是j点，也就是在j点取得最小值。也就是说在j前面的。如下图

因为斜率是递增的( 2*f(i) 递增 )，所以前面的点都用不到，可以出队列(队头处理),那么队尾呢，我们就是tail-1< tail < i 比较，如果slope(tail-1,tail)>slope(tail,i),那么斜率就不是递增的了，所以这样的话要出队尾。

下面是题目的代码

#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
ll dp[50010],sum[50010],q[50010];
int l;
double fi(int i){
     
	return sum[i]+i;
}
double fj(int j){
     
	return sum[j]+j+l+1;
}
double slope(int j,int k){
       //斜率
	double y=dp[j]+fj(j)*fj(j)-dp[k]-fj(k)*fj(k);
	double x=fj(j)-fj(k);
	return y/x;
}
int main()
{
     
	std::ios::sync_with_stdio(false);
	int n;
	while(cin>>n>>l){
     
		for(int i=1;i<=n;i++){
     
			cin>>sum[i];
			sum[i]+=sum[i-1];
		}
		int head=1,tail=1;    //tail=1因为下面的条件是head
		for(int i=1;i<=n;i++){
     
			//head
			while(head<tail&&slope(q[head],q[head+1])<=2*fi(i))  head++;   //队头操作
			int j=q[head];
			dp[i]=dp[j]+(fi(i)-fj(j))*(fi(i)-fj(j));  //转移
			while(head<tail&&slope(q[tail-1],q[tail])>=slope(i,q[tail-1])) tail--;		//队尾操作
			q[++tail]=i;
			cout<<dp[i]<<endl;
		}
		printf("%lld\n",dp[n]);
	}
}

最后总结：斜率优化就是因为i和j在一起不能只用单调队列来优化，具体看要求什么值，再去看斜率怎么样。
总结下写法，就是求斜率，就是将dp[i]=f(j)这样的，写出f(j)

最后上一道题https://atcoder.jp/contests/dp/tasks/dp_z
斜率优化也不能只套模板，特别的边界，初始化的时候特别处理
也是斜率优化的dp，代码如下：

#include 
#include 
#include 
#include 
#define  ll long long
#define size 200020
using namespace std;
ll a[size],q[size];
ll dp[size];
double slope(int j,int k) {
     
	double y=dp[j]+a[j]*a[j]-dp[k]-a[k]*a[k];
	double x=a[j]-a[k];
	return y/x;
}
int main()
{
     
	int n;
	ll c;
	while(cin>>n>>c){
     
		for(int i=1;i<=n;i++)
			cin>>a[i];
		dp[0]=0;
		int head=1,tail=1;
		q[head]=1;  	//这里注意初始化，因为第一块是不消耗的
		for(int i=2;i<=n;i++){
     
			while(head<tail&&slope(q[head],q[head+1])<=2*a[i]) head++;
			int j=q[head];
			dp[i]=dp[j]+c+(a[i]-a[j])*(a[i]-a[j]);
			while(head<tail&&slope(q[tail-1],q[tail])>=slope(q[tail],i)) tail--;
			q[++tail]=i;
		}
		cout<<dp[n]<<endl;
	}
}