二分图最大匹配（最大流）

先举个例子，有N台计算机和K个任务，每个计算机只能执行一个任务，但可以执行多种任务。现在给出N和K，和其关系，求出最多能处理的任务数。

这就是典型的二分图，整张图被分为两半，一半是电脑，一半是任务。

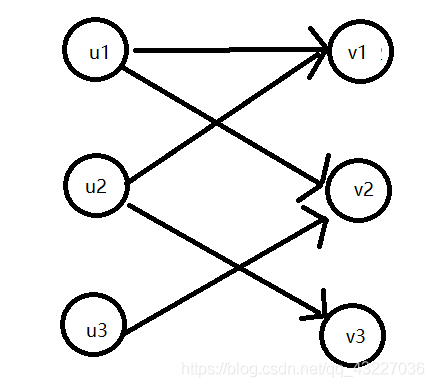
这是多源点多汇点问题，我们只要加上两个点后，就可以把问题转换为单源单汇点问题。
如图：

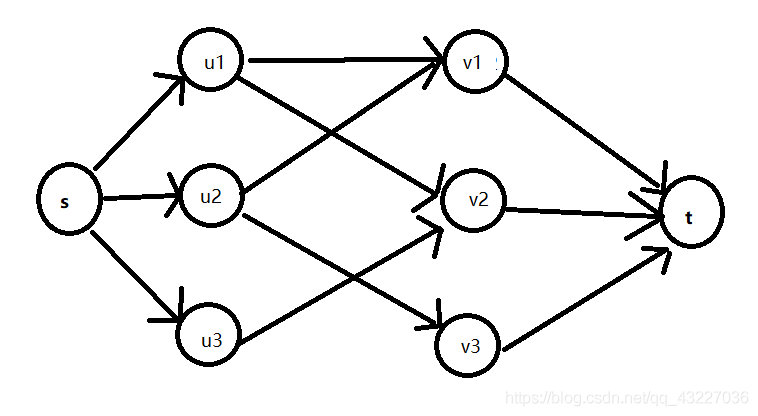
看到这个图片大家肯定特别的熟悉，这不就转换为了我们的最大流问题了，权值只不过都是固定的1而已，其他的都是套模板就行。下面代码是FF，可以把其换位Dicnic，不过这道题FF也过了。

下面是poj3041例题AC代码：http://poj.org/problem?id=3041

#include 
#include 
#include 
#include  

using namespace std;

const int MAX_N = 500001;
const int INF = 0x3f3f3f3f; 

struct edge
{
	int to, cap, ves;
};

vector G[MAX_N];
bool used[MAX_N];
int N, K;

void add_edge(int from, int to, int cost)
{
	struct edge e = {to, cost, G[to].size()};
	
	G[from].push_back(e);
	
	struct edge v = {from, 0, G[from].size() - 1};
	
	G[to].push_back(v);
}

int dfs(int v, int t, int f)
{
	if (v == t)
	{
		return f;
	}
	
	used[v] = true;
	
	for (int i=0; i 0)
		{
			int d = dfs(e.to, t, min(f, e.cap));
			
			if (d > 0)
			{
				e.cap -= d;
				G[e.to][e.ves].cap += d;
				return d;
			}
		}
	}
	
	return 0;
}

int max_flow(int s, int t)
{
	int flow = 0;
	
	for (;;)
	{
		memset(used, 0, sizeof(used));
		
		int f = dfs(s, t, INF);
		
		if (f == 0) 
		{
			return flow;
		}
		
		flow+=f;
	}
}

void slove()
{
	int s = N+K+1, t = s+1;

	for (int i=1; i<=N; i++)
	{
		add_edge(s, i, 1);
	}
	
	for (int i=1; i<=K; i++)
	{
		add_edge(N+i, t, 1);
	}
	
	for (int i=0; i> a >> b;
		
		add_edge(a, N+b, 1);
	} 
		
	printf("%d\n", max_flow(s, t));
}

int main()
{
	scanf("%d %d", &N, &K);
	
	slove();
	
	return 0;
}