c++排序算法总结

排序分类：

• 按照排序数据是否都在内存分为内排序和外排序。
• 按照是否通过比较方式排序分为比较排序和非比较排序。（基数排序基于桶分配）
• ​​​​​​​按照排序前后原

目录

桶排序（非基于比较的排序）

基数排序（基于分配的排序）

选择排序 

冒泡排序

插入排序

自底向上合并排序

希尔排序

---

桶排序（非基于比较的排序）

桶排序是最简单的排序，不允许反驳，听名字挺高大上，你在编程中肯定使用过这种排序方法。

原理：假如你有一个数组[2 8 5 6 9 2 2 1 ],怎么将排序后的数组打印出来呢？假设这个数组中的最大元素值为max。我们先排列一些桶，按0 1 2 3 .......max，然后将各个数组中的元素投放到各个桶中，现在结果是:

   桶0:  0     桶1:  1     桶2:  3     桶3:  0     桶4:  0     桶5:  1     桶6:  1     桶7:  0     桶8:  1     桶9:  1 

其中，桶中存放的是这个元素在数组中出现的次数，排序时，我们依次从桶中取出元素，将其打印出来（比如，桶2中有3个元素，就打印3个3）

缺点：如此简单的排序算法，缺点就不言而喻了吧，首先在排序前你需要知道当前待排序的数组中最大元素是什么，否则在创建桶序列的时候会造成空间的浪费，换言之，就是这种排序算法所能使用的场景非常有限，仅当元素之间的值相差不大的时候使用。平时还是不推荐使用的！！！

---

基数排序（基于分配的排序）

原理：

       试想，生活中我们怎么对22 23 这两个元素排序呢，你肯定一看就发现了，这两个元素十位数是相同的，仅个位数字不同，按照个位数字排序即可得到正常的排序。那么，对于99，89我们是怎么排序的呢，对了，根据十位数字排序就可以了。进一步，对于65 56 45我们可以怎样排序呢，按照上面得到的启示，我们先对个位进行排序得到65 56 45，再对十位进行排序得到45 56 65 。明白了原理，就来动手实现吧！！

---

选择排序 

原理：将待排序的数组分成【有序区，无序区】，每次循环之前变量i之前为有序区，变量j遍历无序区，选择当前无序区中的最小元素放到有序区的末尾（变量i的位置）

原理图：
       假设对数组[7 8  6 2]排序：

                                   [7 8  6 2]

              ①交换7，2：[2 8 6 7]

              ②交换8，6：[2 6 8 7]
              ③交换7，8：[2 6 7 8]

              ④ 得到结果 :[2 6 7 8]

   比较次数：n*(n+1)/2    O(n^2)

   元素赋值次数：0~ 3n次   （执行一次swap需要赋值三次）       

#include
using namespace std;
int main(){
	int n;
	cin>>n;
	int arr[n];
	for(int i=0;i>arr[i];
	}
	 int curMin;
	 int minPos;
	 int temp;
	for(int i=0;i

一句话总结选择排序：每次从无序区选择最小元素与临界元素进行交换。

---

冒泡排序

原理：以较大数值元素沉底为例：相邻元素两两相比，能保证一趟之后，都将当前最大值沉底。

原理图：

 假设对数组[4 3  2 1]排序：

                                    [4 3  2 1]

              ①交换4，3：[ 3 4 2 1]

              ②交换4，2：[3 2 4 1]
              ③交换4，1：[3 2 1 4]    第一趟结束

              ①交换3，2：[2 3 1 4]   

              ②交换3，1：[2 1 3 4]    第二趟结束
              

              ①交换2，1：[1 2 3 4]    第三趟结束

              ①                  [ 1 2 3 4]    第四趟结束

 

   比较次数：n*(n-1)/2    O(n^2)

   元素赋值次数：0~ 3（n*(n-1)/2）次   （执行一次swap需要赋值三次）    

#include
using namespace std;
int main(){
   int n;
   cin>>n;
   int a[n];
   int temp;
   for(int i=0;i>a[i];
   }
   for(int i=0;ia[j+1]){
   			temp=a[j];
   			a[j]=a[j+1];
   			a[j+1]=temp;
		   }
	   }
   }
   
   for(int i=0;i

一句话总结冒泡排序：相邻之间比较，重的沉底

---

插入排序

原理：从数组第1个元素开始，它自然是排序好的。

           接着把第2个元素插入到第1个元素前面或者后面,至此，前两个元素已经排好序了。

           再接着把第3个元素插入到前两个元素之间合适的位置，至此，前三个元素是排好序......

与选择排序的不同点：

      选择排序是从后面精挑细选选出最小元素和分界点元素互换实现排序。而插入排序是把分界点的元素在前面已经排序的序列中精挑细选一个位置插入。

原理图：
 假设对数组[4 2 3 1]进行插入排序，首先将数组分成[4      2 3 1],将分界点的2插入到前方得到[2 4    3 1],再将分界点的3插入到前面合适位置，得到：[2 3 4     1]，最后，将1插入到前面合适位置得到[1 2 3 4],至此，排序结束。

比较次数：当整个序列一开始就按照非降序排列时，假设当前分界点在i处，则直接将a[i]与a[i-1]比较即可。

最好情况比较次数为n-1次，最坏情况比较次数为n*(n-1)/2。

赋值次数：赋值次数为比较次数加上n-1，因为每次比较都要将大元素往后挪一个位置，找到合适位置插入需要一次。

#include
using namespace std;
int main(){
  int n;
  cin>>n;
  int a[n];
  for(int i=0;i>a[i];
  }
  int curInsertValue;
  int j;      //j指向的元素若大于当前要插入的值，就将a[j]的值后传给a[j+1]，表示要插入的地方在此之前，腾出一个位置用来插入 
  for(int i=1;i0 && a[j]>curInsertValue){
  		a[j+1]=a[j];
  		j--;
	  }       //结束while循环时，j此时指向的单元值小于等于要插入的值，此时将要插入的值插入在j之后即可 
	  a[j+1]=curInsertValue; 
  }
  
  for(int i=0;i

一句话总结插入排序：把分界点处的值插入到前面按顺序排列的序列中合适位置。

---

自底向上合并排序

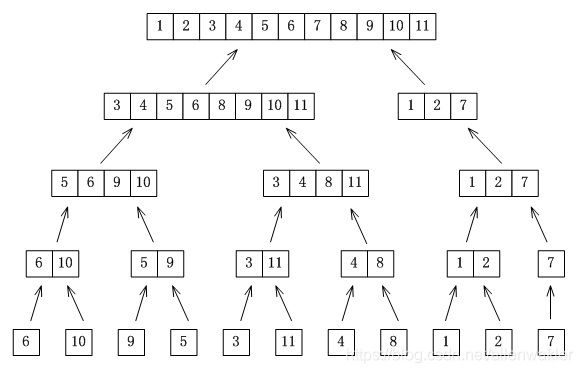
原理：将数组中元素两两合并排序，再四四合并排序，再八八合并排序......不足合并长度的单独处理。

原理图：

 

在我的实现中，使用头文件中的sort()函数代替了合并排序中的函数merge()。

使用sort函数，需要传进去两个参数，开始排序的地址和结束地址，函数将对[开始地址，结束地址）之间的元素进行排序。

而使用merge()函数进行合并排序时应给出数组，两个要合并的短数组的开始地址，结束地址，将对其中间元素进行排序。

比较次数：O（n*logn）

#include
#include
using namespace std;

void printArr(int a[]){
	cout<<"排序之后的结果是"<arrLen)
	        break;
   }
   cout<

---

希尔排序

原理：希尔排序是在插入排序的基础上进行改进得到的，又名减小增量法。在插入排序中，我们在进行插入时看成是步长为1的插入，而在希尔排序中步长是变化的而且越来越小的（一般从数组长度一半开始变化，最后变为步长为1的插入排序）。

↓是插入排序的关键代码，在代码第五行我们发现，在进行插入挪位置的时候，每次是把数据向后挪一个位置，while循环结束后表示找到了合适的插入点，此时再将需要插入的数据插入。

for(int i=1;i0 && a[j]>curInsertValue){
  		a[j+1]=a[j];
  		j--;
	  }       //结束while循环时，j此时指向的单元值小于等于要插入的值，此时将要插入的值插入在j之后即可 
	  a[j+1]=curInsertValue; 
  }

如果能理解上面，那么希尔排序其实就对你不是很难理解了。

↓是希尔排序的核心代码，可以清楚得看到代码是由三重循环构成，最外面一层循环是用来缩小步长的，中间一层循环是用来pick当前需要进行插入操作的元素的，而最内层的while循环是通过元素挪位置寻找合适插入点的！！哈哈，这样对比起来学习是不是就很一目了然了？我们不难观察到，这里挪位置是以gap为单位进行的，整个过程看起来就像是先大致排一下序，通过缩小步长，一步步将排序精准。

for (int gap = floor(len / 2); gap > 0; gap = floor(gap / 2)) {
		for (int i = gap; i < len; i++) {
			int j = i;
			int current = a[i];
			while (j - gap >= 0 && current < a[j - gap]) {
				a[j] = a[j - gap];
				j = j - gap;
			}
			a[j] = current;
		}
}

原理图：下面，我就以最经典的希尔排序的一个例子来讲解整个过程。

希尔排序就是假定每轮排序开始之前，数组的前步长个元素是有序的，我们将剩余元素插入数组中的合适位置，步长依次取arr.len/2,arr.len/4,arr.len/8........步长终止为1，此时退化成插入排序，所以能保证最后的数组是整体有序的，至于比插入排序多此一举，读者可以好好体会一下多此一举的好处在哪里。
 

下图中用粗体表示排序开始时默认有序的序列：（注意，挪位置过程以Gap为单位进行，而不是像插入排序一样一比对）

假设最初数组为：[84,83,88,87,61,50,70,60,80,99]       

数组长度10   

*对于每一步操作之后的注解，只要当前待插入元素比判定有序的写相应位置元素大，就不移动（联系插入排序想为啥！！）

gap选定为5

          将50插入：[50 83 88 87 61 84 70 60 80 99]     比较50 与84，移动一次

          将70插入：[50 70 88 87 61  84 83 60 80 99]     比较70 与83，移动一次

          将60插入：[50 70 60 87 61  84 83 88 80 99]      比较60 与88，移动一次

          将80插入：[50 70 60 80 61  84 83 88 87 99]      比较80 与87，移动一次

          将99插入：[50 70 60 80 61  84 83 88 87 99]       比较99 与61，不移动

gap缩小为2

                            [50 70 60 80 61  84 83 88 87 99]

          将60插入：[60 70 50 80 61  84 83 88 87 99]   比较60 与50，移动一次

          将80插入：[60 70 50 80 61  84 83 88 87 99]    比较80 与70，不移动

          将61插入：[60 70 50 80 61  84 83 88 87 99]    比较61与50 60，不移动

         将84插入：[60 70 50 80 61  84 83 88 87 99]    比较84 与80 70，不移动

         将83插入：[60 70 50 80 61  84 83 88 87 99]     比较83 与61 50 60，不移动

         将88插入：[60 70 50 80 61  84 83 88 87 99]     比较88 与84 80 70，不移动

         将87插入：[60 70 50 80 61  84 83 88 87 99]     比较87 与83 61 50 60，不移动

         将99插入：[60 70 50 80 61  84 83 88 87 99]      比较99 与88 84 80 70，不移动

     可以看出，第二趟的时候需要移动的次数就已经很少很少了，联想上面的问题，你应该知道为啥希尔排序要‘’多此一举了‘’吧？

在计算机中遍历所需的时间必然比交换所需时间小得多！！！

gap缩小为1（退化成插入排序）

                             [60 70 50 80 61  84 83 88 87 99] 

          将70插入：[60 70 50 80 61  84 83 88 87 99]      比较70 与60，不移动

          将50插入：[50 60 70 80 61  84 83 88 87 99]      比较50 与60 70 移动两次，插入

          将80插入：[50 60 70 80 61  84 83 88 87 99]      比较80 与70 60 50  不移动

          将61插入：[50 60 70 80 61  84 83 88 87 99]      比较61 与 80 70 60 50  移动两次，插入

         将61插入：[50 60  61 70 80 84 83 88 87 99]      比较61 与 80 70 60 50  移动两次，插入

         将84插入：[50 60  61 70 80 84 83 88 87 99]      比较84 与 80 70 61 60 50  不移动

         将83插入：[50 60  61 70 80 83 84 88 87 99]      比较83 与84 80 70 61 60 50  移动一次，插入

        将88插入： [50 60  61 70 80 83 84 88 87 99]        比较88 与84 83 80 70 61 60 50  不移动

       将87插入： [50 60  61 70 80 83 84 87 88 99]        比较87 与 88 84 83 80 70 61 60 50  移动一次，插入

       将99插入： [50 60  61 70 80 83 84 87 88 99]        比较99与 88 87 84 83 80 70 61 60 50  不移动

结束！！！！！

 

#include
#include
using namespace std;

void printArr(int a[]) {
	int len = 10;
	for (int i = 0; i < 10; i++) {
		cout << a[i] << " ";
	}
	cout << endl;
}

int main() {
	int a[10] = {84,83,88,87,61,50,70,60,80,99 };
	int len = 10;
	for (int gap = floor(len / 2); gap > 0; gap = floor(gap / 2)) {
		cout << "当前的gap值是：" << gap << endl << endl;;
		for (int i = gap; i < len; i++) {
			int j = i;
			cout << "当前的i值是：" << i << "   " << "当前的j值是：" << j << endl;
			int current = a[i];
			cout << "当前的current值是：" << current <= 0 && current < a[j - gap]) {
			cout << "赋值之前a[j-gap]a[j]：" << a[j-gap] <<" "<< a[j]<< endl;
				a[j] = a[j - gap];
				j = j - gap;
			cout << "赋值之后a[j-gap]a[j]：" << a[j- gap] << " " << a[j] << endl;
			}
			a[j] = current;
			cout << "a[j]：" << a[j] << endl;
			printArr(a);
		}
	}
	
	return 0;
	}
	

一句话总结希尔排序：缩小步长的插入排序，其中每次变换步长后默认有序序列和挪位置的跨度都会改变。

---

 

 

归并排序，堆排序，基于二叉树的排序相关内容后续补齐！