线段树算法详解

线段树基本概念

线段树，顾名思义就是由一个一个线段组成的一颗树，每个结点都是一个线段（叶子结点是单元结点），那么每个结点应该包括：

• 区间左右端点。
• 区间要维护的信息（视情况而定）。

即每个结点是一个结构体。区间上可以进行区间查询，修改，求和等操作。线段树还是一颗二叉搜索树。其主要用于高效解决连续区间的动态查询问题。

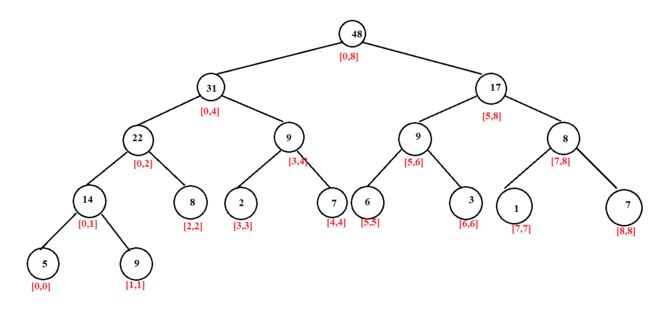
结构图：

其中结点的数字代表第几个结点，红色数字代表这个点表示的区间范围。

由结构图可知：

1. 每个几点的左孩子区间的范围为[l,mid]，右孩子为[mid+1,r]
2. 对于结点k，左孩子结点为2*k，右孩子为2*k+1。

线段树基础操作

1.结构体定义：

 

struct node
{
    int l,r,w;
//l，r分别表示区间左右端点，w表示区间和
}tree[4*n+1];//开四倍的空间

 

2.建树

思想：

1. 对于二分到每一个结点，给它的左右端点确定范围。
2. 如果是叶子结点，存储要维护的信息。
3. 状态合并。

void build(int l,int r,int k)
{
    tree[k].l=l;tree[k].r=r;
    if(l==r)//叶子节点 
    {
        scanf("%d",&tree[k].w);
        return ; 
    }
    int m=(l+r)/2;
    build(l,m,k*2);//左孩子 
    build(m+1,r,k*2+1);//右孩子 
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//状态合并，此结点的w=两个孩子的w之和 
}

3.单点查询（二分法）

思想：

1. 如果当前枚举的点左右端点相等，即叶子节点，就是目标节点。
2. 如果不是，因为这是二分法,所以设查询位置为x，当前结点区间范围为了l，r，中点为mid，则如果x<=mid，则递归它的左孩子，否则递归它的右孩子。

void ask(int k)
{
    if(tree[k].l==tree[k].r) //当前结点的左右端点相等，是叶子节点，是最终答案 
    {
        ans=tree[k].w;
        return ;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) ask(k*2);//目标位置比中点靠左，就递归左孩子 
    else ask(k*2+1);//反之，递归右孩子 
}

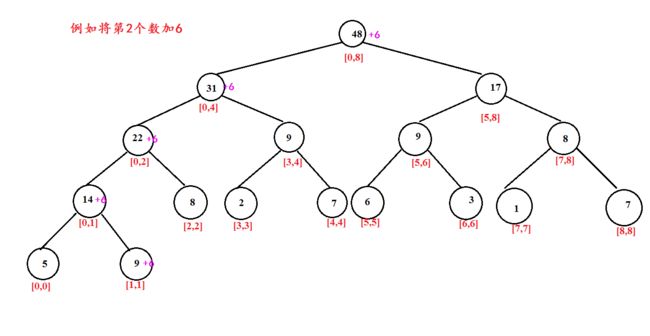
4.单点修改

思想：

1. 首先利用单点查询的思想找到目标结点x。
2. 利用建树时合并的思想将目标结点以及其父节点进行修改。

void add(int k)
{
    if(tree[k].l==tree[k].r)//找到目标位置 
    {
        tree[k].w+=y;
        return;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) add(k*2);
    else add(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//所有包含结点k的结点状态更新 
}

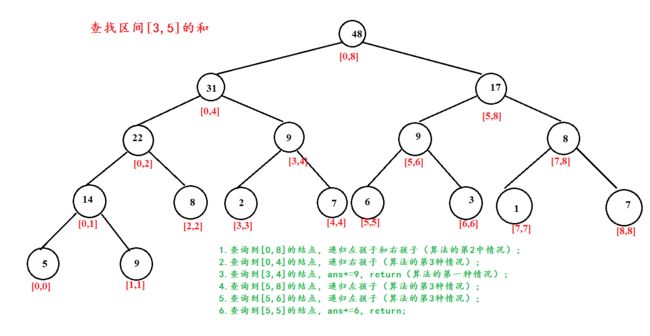
5.区间查询

思想：

当前区间和待查询区间一共有三种情况：

1.当前结点区间的值全部是带查询区间的一部分，则直接加上当前区间的区间和。

2.当前结点区间包含了带查询的区间，则继续递归左右子区间，直至情况1或情况3。

3.当前结点区间与带查询区间交叉，继续递归直至情况1。

void sum(int k)
{
    if(tree[k].l>=x&&tree[k].r<=y) 
    {
        ans+=tree[k].w;
        return;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) sum(k*2);
    if(y>m) sum(k*2+1);
}

6.区间修改

 如果数据量很大，要求将某个很大的区间的每个元素进行修改，那么其时间复杂度将会非常大，那么线段树算法的意义就不在了，而且修改某个区间的元素之后不一定会用到该区间的孩子结点的信息，因此为了降低复杂度，这里引入懒标记--线段树的精髓。

• 懒标记，顾名思义，就是懒，用到的时候动，不用的时候就不动。
• 作用就是存储这个结点的修改信息，暂时不把修改的信息传到子节点。递归到这个结点时，只更新这个结点的状态，并把当前的更改值累积到标记中。
• 当需要递归这个结点的子结点时，标记传递给子节点。
• 下传递时需要进行的操作：
  1. 当前结点的懒标记累积到子节点的懒标记中。
  2. 修改子节点的状态。
  3. 父节点的懒标记清0。
• 下面有例子。

在原结构体中增加一个新的变量f，作为懒标记：

struct node
{
       int l,r,w;//l，r分别表示区间左右端点，w表示区间和
       int f;
}tree[4*n+1];

懒标记操作函数：

void down(int k)
{
    tree[k*2].f+=tree[k].f;
    tree[k*2+1].f+=tree[k].f;
    tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
    tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
    tree[k].f=0;
}

因此在上述所有操作函数中需要加上一句

if(tree[k].f)  down（k）

区间修改代码：

void add(int k)
{
    if(tree[k].l>=a&&tree[k].r<=b)//当前区间全部对要修改的区间有用 
    {
        tree[k].w+=(tree[k].r-tree[k].l+1)*x;//(r-1)+1区间点的总数
        tree[k].f+=x;
        return;
    }
    if(tree[k].f) down(k);//懒标记下传。只有不满足上面的if条件才执行，所以一定会用到当前节点的子节点 
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) add(k*2);
    if(b>m) add(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//更改区间状态 
}

完整代码：

#include
using namespace std;
int n,p,a,b,m,x,y,ans;
struct node
{
    int l,r,w,f;
}tree[400001];
inline void build(int k,int ll,int rr)//建树 
{
    tree[k].l=ll,tree[k].r=rr;
    if(tree[k].l==tree[k].r)
    {
        scanf("%d",&tree[k].w);
        return;
    }
    int m=(ll+rr)/2;
    build(k*2,ll,m);
    build(k*2+1,m+1,rr);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;
}
inline void down(int k)//标记下传 
{
    tree[k*2].f+=tree[k].f;
    tree[k*2+1].f+=tree[k].f;
    tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
    tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
    tree[k].f=0;
}
inline void ask_point(int k)//单点查询
{
    if(tree[k].l==tree[k].r)
    {
        ans=tree[k].w;
        return ;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) ask_point(k*2);
    else ask_point(k*2+1);
}
inline void change_point(int k)//单点修改 
{
    if(tree[k].l==tree[k].r)
    {
        tree[k].w+=y;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) change_point(k*2);
    else change_point(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w; 
}
inline void ask_interval(int k)//区间查询 
{
    if(tree[k].l>=a&&tree[k].r<=b) 
    {
        ans+=tree[k].w;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) ask_interval(k*2);
    if(b>m) ask_interval(k*2+1);
}
inline void change_interval(int k)//区间修改 
{
    if(tree[k].l>=a&&tree[k].r<=b)
    {
        tree[k].w+=(tree[k].r-tree[k].l+1)*y;
        tree[k].f+=y;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) change_interval(k*2);
    if(b>m) change_interval(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;
}
int main()
{
    scanf("%d",&n);//n个节点 
    build(1,1,n);//建树 
    scanf("%d",&m);//m种操作 
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&p);
        ans=0;
        if(p==1)
        {
            scanf("%d",&x);
            ask_point(1);//单点查询,输出第x个数 
            printf("%d",ans);
        } 
        else if(p==2)
        {
            scanf("%d%d",&x,&y);
            change_point(1);//单点修改 
        }
        else if(p==3)
        {
            scanf("%d%d",&a,&b);//区间查询 
            ask_interval(1);
            printf("%d\n",ans);
        }
        else
        {
             scanf("%d%d%d",&a,&b,&y);//区间修改 
             change_interval(1);
        }
    }
}

 

 

 

参考博客：https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html

转载于:https://www.cnblogs.com/LMIx/p/10701845.html