动态规划求最长递增子序列
最长递增子序列问题是一个很基本、较常见的小问题,但这个问题的求解方法却并不那么显而易见,需要较深入的思考和较好的算法素养才能得出良好的算法。由于这个问题能运用学过的基本的算法分析和设计的方法与思想,能够锻炼设计较复杂算法的思维,我对这个问题进行了较深入的分析思考,得出了几种复杂度不同算法,并给出了分析和证明。
一, 最长递增子序列问题的描述
设L=
二, 第一种算法:转化为LCS问题求解
设序列X=
最长公共子序列问题用动态规划的算法可解。设Li=< a1,a2,…,ai>,Xj=< b1,b2,…,bj>,它们分别为L和X的子序列。令C[i,j]为Li与Xj的最长公共子序列的长度。则有如下的递推方程:
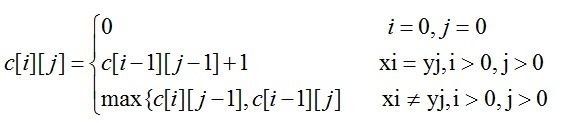
#include 这可以用时间复杂度为O(n2)的算法求解。求最长递增子序列的算法时间复杂度由排序所用的O(nlogn)的时间加上求LCS的O(n2)的时间,算法的最坏时间复杂度为O(nlogn)+O(n2)=O(n2)。
三, 第二种算法:动态规划法
设f(i)表示L中以ai为末元素的最长递增子序列的长度。则有如下的递推方程:
f[i] = max(f[j]) + 1
这个递推方程的意思是,在求以ai为末元素的最长递增子序列时,找到所有序号在L前面且小于ai的元素aj,即j
#include 这个算法有两层循环,外层循环次数为n-1次,内层循环次数为i次,算法的时间复杂度T(n)=O(n2)。这个算法的最坏时间复杂度与第一种算法的阶是相同的。但这个算法没有排序的时间,所以时间复杂度要优于第一种算法。
这个方法也最容易想到也是最传统的解决方案,对于该方法和LIS,有以下两点说明:
- 由LIS可以衍生出来最长非递减子序列,最长递减子序列,道理是一样的。
- 对于输出序列,也是可以再申请一数组pre[i]记录子序列中array[i]的前驱,道理跟本节的实现也是一样的
四, 对第二种算法的改进
《编程之美》对于这个方法有提到,不过它的讲解我看得比较难受,好长时间才明白,涉及到的数组也比较多,除了源数据数组,有LIS[i]和MaxV[LIS[i]],后来发现编程之美中的这个数组MaxV[LIS[i]]在记录信息上其实是饶了弯的,因为我们在寻找某一长度子序列所对应的最大元素最小值时,完全没必要通过LIS[i]去定位,即没必要与数据arr[i]挂钩,直接将MaxV[i]的下标作为LIS的长度,来记录最小值就可以了(表达能力太次,囧。。。),一句话,就是不需要LIS[i]这个数组了,只用MaxV[i]即可达到效果,而且原理容易理解,代码表达也比较直观、简单。
下面说说原理:
目的:我们期望在前i个元素中的所有长度为len的递增子序列中找到这样一个序列,它的最大元素比arr[i+1]小,而且长度要尽量的长,如此,我们只需记录len长度的递增子序列中最大元素的最小值就能使得将来的递增子序列尽量地长。
方法:维护一个数组MaxV[i],记录长度为i的递增子序列中最大元素的最小值,并对于数组中的每个元素考察其是哪个子序列的最大元素,二分更新MaxV数组,最终i的值便是最长递增子序列的长度。这个方法真是太巧妙了,妙不可言。
#include
using namespace std;
/* 最长递增子序列 LIS
* 设数组长度不超过 30
* DP + BinarySearch
*/
int MaxV[30]; /* 存储长度i+1(len)的子序列最大元素的最小值 */
int len; /* 存储子序列的最大长度 即MaxV当前的下标*/
/* 返回MaxV[i]中刚刚大于x的那个元素的下标 */
int BinSearch(int * MaxV, int size, int x)
{
int left = 0, right = size-1;
while(left <= right)
{
int mid = (left + right) / 2;
if(MaxV[mid] <= x)
{
left = mid + 1;
}else
{
right = mid - 1;
}
}
return left;
}
int LIS(int * arr, int size)
{
MaxV[0] = arr[0]; /* 初始化 */
len = 1;
for(int i = 1; i < size; ++i) /* 寻找arr[i]属于哪个长度LIS的最大元素 */
{
if(arr[i] > MaxV[len-1]) /* 大于最大的自然无需查找,否则二分查其位置 */
{
MaxV[len++] = arr[i];
}else
{
int pos = BinSearch(MaxV,len,arr[i]);
MaxV[pos] = arr[i];
}
}
return len;
}
void main()
{
int arr[] = {1,-1,2,-3,4,-5,6,-7};
/* 计算LIS长度 */
printf("%d\n",LIS(arr,sizeof(arr)/sizeof(int)));
}