统计学基础(二):三个基本抽样分布
此为本人学习笔记,不具备参考价值,禁止任何形式的传播
1.基本概念
总体:研究对象某项指标的全部。
样本:所研究对象若干个体,称为样本。记作 ( x 1 , x 2 , … ) (x_1,x_2,\ldots) (x1,x2,…)
如果
- x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x1,x2,…,xn相互独立
- x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x1,x2,…,xn与总体 x x x分布相同
称 ( x 1 , x 2 , … , x n ) (x_1,x_2,\dots,x_n) (x1,x2,…,xn)为简单随机样本。
统计量:称 ( x 1 , x 2 , … , x n ) (x_1,x_2,\dots,x_n) (x1,x2,…,xn)样本的无参函数为统计量。
e g eg eg: x 1 , x 2 , x 3 3 \frac{x_1,x_2,x_3}{3} 3x1,x2,x3 ✓ ✓ ✓ \quad x 1 2 + x 2 2 + x 3 2 ✓ x_1^2+x_2^2+x_3^2✓\quad x12+x22+x32✓ a x 1 + x 2 + x 3 ✗ ax_1+x_2+x_3✗ ax1+x2+x3✗
重要统计量
1.样本均值
x ˉ = x 1 + x 2 + ⋯ + x n n \bar x=\frac{x_1+x_2+\dots+x_n}{n} xˉ=nx1+x2+⋯+xn
2.样本方差
S 2 = 1 n ∑ i − 1 n ( x i 2 − x ˉ ) 2 S^2=\frac{1}{n}\sum_{i-1}^{n}{(x_i^2-\bar x)^2} S2=n1i−1∑n(xi2−xˉ)2
3.样本的 k k k阶原点矩
A k = 1 n ∑ i = 1 n x i k ( k = 1 , 2 , 3 , … ) A_k=\frac{1}{n}\sum_{i=1}^{n}{x_i^k}\quad(k=1,2,3,\dots) Ak=n1i=1∑nxik(k=1,2,3,…)
2.三个抽样分布
统计量的分布称为抽样分布
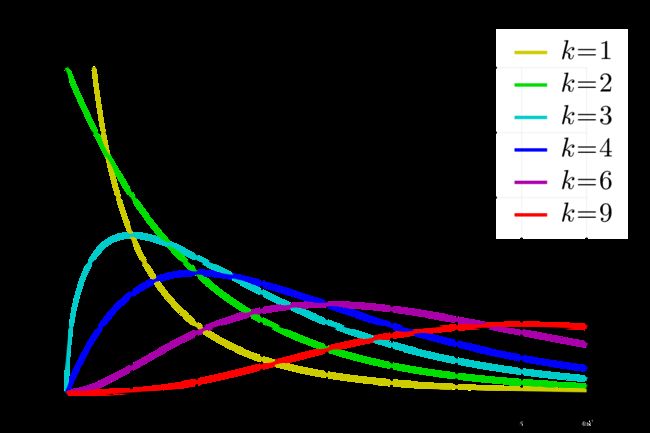
(一) χ 2 − \chi^2- χ2−分布
-
定义: x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x1,x2,…,xn独立同分布于 N ( 0 , 1 ) N(0,1) N(0,1),称
x 1 2 + x 2 2 + ⋯ + x n 2 = z ∼ χ 2 ( n ) x_1^2+x_2^2+\dots+x_n^2=z \sim \chi^2(n) x12+x22+⋯+xn2=z∼χ2(n)
-
性质:
( 1 ) x ∼ N ( 0 , 1 ) , 则 x 2 ∼ χ 2 ( 1 ) (1)\quad x\sim N(0,1),则x^2\sim \chi^2(1) (1)x∼N(0,1),则x2∼χ2(1)
( 2 ) X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) , X 和 Y 相 互 独 立 , 则 X + Y ∼ χ 2 ( m + n ) (2)\quad X\sim \chi^2(m),Y\sim \chi^2(n),X和Y相互独立,则X+Y \sim \chi^2(m+n) (2)X∼χ2(m),Y∼χ2(n),X和Y相互独立,则X+Y∼χ2(m+n)
( 3 ) x ∼ χ 2 ( n ) , 则 E x = n , D x = 2 n (3)\quad x\sim \chi^2(n),则Ex=n,Dx=2n (3)x∼χ2(n),则Ex=n,Dx=2n
例:设 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3是来自总体 N ( 0 , 4 ) 的 样 本 , 已 知 N(0,4)的样本,已知 N(0,4)的样本,已知 a x 1 2 + b ( 2 x 2 + x 3 ) 2 ∼ χ 2 ( n ) ax_1^2+b(2x_2+x_3)^2\sim\chi^2(n) ax12+b(2x2+x3)2∼χ2(n),求 a , b , n a,b,n a,b,n的值
解: x 1 ∼ N ( 0 , 4 ) ⟹ x_1\sim N(0,4) \Longrightarrow x1∼N(0,4)⟹ x 1 2 \frac{x_1}{2} 2x1 ∼ N ( 0 , 1 ) \sim N(0,1) ∼N(0,1)
2 x 2 + x 3 ∼ N ( 0 , 20 ) ⟹ 2x_2+x_3 \sim N(0,20) \Longrightarrow 2x2+x3∼N(0,20)⟹ 2 x 1 + x 3 20 \frac{2x_1+x_3}{\sqrt{20}} 202x1+x3 ∼ N ( 0 , 1 ) \sim N(0,1) ∼N(0,1)
∵ \because ∵ x 1 2 , 2 x 1 + x 3 20 \frac{x_1}{2} ,\frac{2x_1+x_3}{\sqrt{20}} 2x1,202x1+x3 独立
∴ \therefore ∴ 1 4 \frac{1}{4} 41 x 1 2 + x_1^2+ x12+ ( 2 x 1 + x 3 ) 2 20 ∼ χ 2 ( 2 ) \frac{(2x_1+x_3)^2}{20}\sim\chi^2(2) 20(2x1+x3)2∼χ2(2)
∴ a = 1 4 b = 1 20 n = 2 \therefore a=\frac{1}{4}\quad b=\frac{1}{20} \quad n=2 ∴a=41b=201n=2
(二) t − 分 布 t-分布 t−分布
- 定义:若 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) , X , Y 相 互 独 立 , 则 X\sim N(0,1),Y\sim \chi^2(n),X,Y相互独立,则 X∼N(0,1),Y∼χ2(n),X,Y相互独立,则
X Y / n = t ∼ t ( n ) \frac{X}{\sqrt{Y/n}}=t\sim t(n) Y/nX=t∼t(n) - 性质:
( 1 ) i f x ∼ t ( n ) , 则 x 近 似 服 从 N ( 0 , 1 ) , E x = 0 (1)if \quad x\sim t(n),则x近似服从N(0,1),Ex=0 (1)ifx∼t(n),则x近似服从N(0,1),Ex=0
( 2 ) x ∼ t ( n ) , 密 度 函 数 : (2)x\sim t(n),密度函数: (2)x∼t(n),密度函数:

例: X 1 , X 2 X_1,X_2 X1,X2是来自总体 N ( 0 , 4 ) N(0,4) N(0,4)的样本, Y 1 , Y 2 Y_1,Y_2 Y1,Y2是来自总体 N ( 0 , 4 ) N(0,4) N(0,4)的样本, X , Y X,Y X,Y相互独立, X 1 + X 2 Y 1 2 + Y 2 2 \frac{X_1+X_2}{\sqrt{Y_1^2+Y_2^2}} Y12+Y22X1+X2服从什么分布?
解: X 1 + X 2 ∼ N ( 0 , 8 ) , X 1 + X 2 8 ∼ N ( 0 , 1 ) X_1+X_2\sim N(0,8),\frac{X_1+X_2}{\sqrt{8}}\sim N(0,1) X1+X2∼N(0,8),8X1+X2∼N(0,1)
Y 1 2 ∼ N ( 0 , 1 ) , Y 2 2 ∼ N ( 0 , 1 ) \frac{Y_1}{2}\sim N(0,1),\frac{Y_2}{2}\sim N(0,1) 2Y1∼N(0,1),2Y2∼N(0,1)
Y 1 2 + Y 2 2 4 ∼ χ 2 ( 2 ) \frac{Y_1^2+Y_2^2}{4}\sim \chi^2(2) 4Y12+Y22∼χ2(2)
X 1 + X 2 8 Y 1 2 + Y 2 2 4 / 2 ∼ t ( 2 ) \frac{\frac{X_1+X_2}{\sqrt{8}}}{\sqrt{\frac{Y_1^2+Y_2^2}{4}/2}}\sim t(2) 4Y12+Y22/28X1+X2∼t(2)
x 1 + x 2 Y 1 2 + Y 2 2 ∼ t ( 2 ) \frac{x_1+x_2}{\sqrt{Y_1^2+Y_2^2}}\sim t(2) Y12+Y22x1+x2∼t(2)
(三) F − 分 布 F-分布 F−分布
- 定义:若 X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) , X , Y 相 互 独 立 , 则 X\sim \chi^2(m),Y\sim \chi^2(n),X,Y相互独立,则 X∼χ2(m),Y∼χ2(n),X,Y相互独立,则
X / m Y / m = F ∼ F ( m , n ) \frac{X/m}{Y/m}=F\sim F(m,n) Y/mX/m=F∼F(m,n) - 性质
( 1 ) X ∼ F ( m , n ) , 1 X ∼ F ( n , m ) (1)X\sim F(m,n),\frac{1}{X}\sim F(n,m) (1)X∼F(m,n),X1∼F(n,m)
( 2 ) X ∼ F ( m , n ) , 密 度 函 数 : (2)X\sim F(m,n),密度函数: (2)X∼F(m,n),密度函数:

例: X ∼ t ( 2 ) , X 2 服 从 什 么 分 布 X\sim t(2),X^2服从什么分布 X∼t(2),X2服从什么分布
解: ∃ U ∼ N ( 0 , 1 ) , V ∼ χ 2 ( 2 ) , U , V 相 互 独 立 \exist U\sim N(0,1),V\sim \chi^2(2),U,V相互独立 ∃U∼N(0,1),V∼χ2(2),U,V相互独立
X = U V / 2 X=\frac{U}{\sqrt{V/2}} X=V/2U
X 2 = U 2 V / 2 X^2=\frac{U^2}{V/2} X2=V/2U2
∵ U 2 ∼ χ 2 ( 1 ) , V ∼ χ 2 ( 2 ) , 且 U 2 与 V 独 立 \because U^2\sim \chi^2(1),V\sim \chi^2(2),且U^2与V独立 ∵U2∼χ2(1),V∼χ2(2),且U2与V独立
∴ X 2 = U 2 / 1 V / 2 ∼ F ( 1 , 2 ) \therefore X^2=\frac{U^2/1}{V/2}\sim F(1,2) ∴X2=V/2U2/1∼F(1,2)