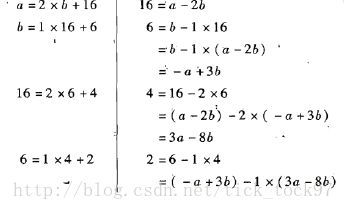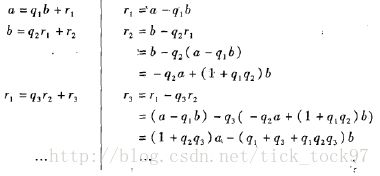数论常用内容——欧几里得算法与扩展欧几里得算法
欧几里得算法
欧几里得算法有一个为更多人所知的名字叫“辗转相除法”,它是用来求解两个数的最大公约数的算法
其计算原理依赖于下面的定理:
定理:
两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。最大公约数(greatest common divisor)缩写为gcd。
即:gcd(a,b) = gcd(b,a mod b) (不妨设a>b 且r=a mod b ,r不为0)
通过这个定理,我们可以很快的求解出两个数的最大公约数
下面我们来看代码
int GCD(int a,int b){
return b?GCD(b,a%b):a;
}用递归的方式写出来,非常的清晰,也很好记,能如此简洁也正是因为利用了之前所说的定理
扩展欧几里得算法
扩展欧几里得算法的思想基于以下定理:
对于不完全为 0 的非负整数 a,b,gcd(a,b)表示 a,b 的最大公约数,必然存在整数对 x,y ,使得 gcd(a,b)=ax+by。
关于这个定理,我们可以看一下一下这个例子(引用自数论概论,机械工业出版社)
这个例子中,左边是欧几里得算法(gcd(60,22)),右边是扩展欧几里得算法(60x+22y=gcd(60,22))
可以看出,通过欧几里得算法的中间商和余数可以解出方程gcd(a,b)=ax+by,那么,为什么可以这样呢?我们来看一个通解的形式
一行行进行,我们可以找到规律:最新余数=a的倍数+b的倍数
我们最后得到的非零余数,他等于gcd(a,b),这就给出了方程gcd(a,b)=ax+by的一组特解
这便是扩展欧几里得算法的思想,下面我们来看代码
int Ex_GCD(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int ans=Ex_GCD(b,a%b,x,y);
int tmp=x;
x=y;
y=tmp-a/b*y;
return ans;
}通过这样的代码,我们就可以很方便的解出方程gcd(a,b)=ax+by的一组特解(x0,y0),它的通解我们可以用以下式子求出:
x = x0 + (b/gcd)*t
y = y0 – (a/gcd)*t
那么,扩展欧几里得算法能干些什么呢?它一般有以下几种用途:
1.求解ax+by=c的整数解
2.求模线性方程求模线性方程ax≡b(mod n)的最小解
3.求乘法逆元
4.求解模方程a^x≡b(mod n)
下面我们来一一介绍
1、求解ax+by=c的整数解
ax+by=gcd(a,b)=g的一组解为(x0,y0),则ax+by=c的一组解为(x0*c/g,y0*c/g)。当c不是g的倍数时无整数解。若(x1,y1)是ax+by=c的一组解,则其任意整数解为(x1+k*bb,y1-k*aa),其中aa=a/gcd(a,b) ,bb=b/gcd(bb),k为任意整数
2、求模线性方程求模线性方程ax≡b(mod n)的最小解
这个直接看代码吧非常好理解
int modequ(int a,int b,int n){
int x,y,d,b1;
d=Ex_GCD(a,n,x,y);
if(b%d) return -1;
b1=(n/d)<0?-n/d:n/d;
x*=b/d;
return (x%b1+b1)%b1;
}3、求乘法逆元
逆元:a*x≡1(mod m),其中,x为a关于m的逆元
一开始看到这句话大家可能会比较懵,就我的经验来理解,逆元的用途就是:如果一个数a要除以一个很大的数b,两个数都模m,那么,这个运算等价于a乘以b关于m的逆元
下面来看代码
int inv(int a,int m){
int x,y;
int gcd=Ex_GCD(a,m,x,y);
if(1%gcd!=0) return -1;
x*=1/gcd;
m=abs(m);
int ans=x%m;
if(ans<=0) ans+=m;
return ans;
}4、求解模方程a^x≡b(mod n)
这个也不多说,直接上代码
//n为素数,无解返回-1
int log_mod (int a,int b,int n){
int m,v,e=1,i;
m=ceil(sqrt(n+0.5));
v=inv(pow_mod(a,m),n);
map<int,int>x;
x[1]=0;
for(i=1;iif(!x.count(e))x[e]=i;
}
for(i=0;iif(x.count(b))return i*m+x[b];
b=(b*v)%n;
}
return -1;
} 到此,欧几里得算法与扩展欧几里得算法的介绍就结束了,题目推荐大家可以去百度一下,有很多题目分类文章,我在此就不列举了