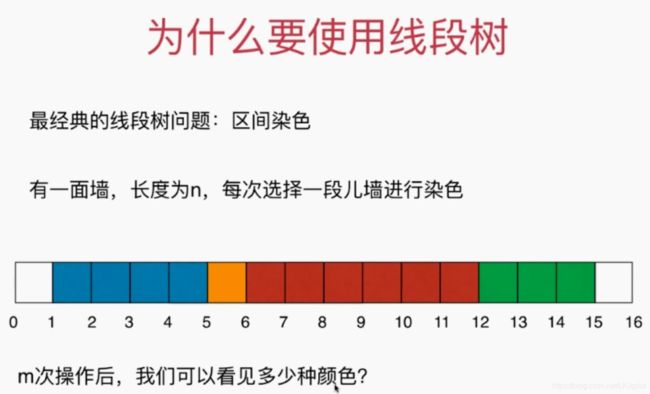
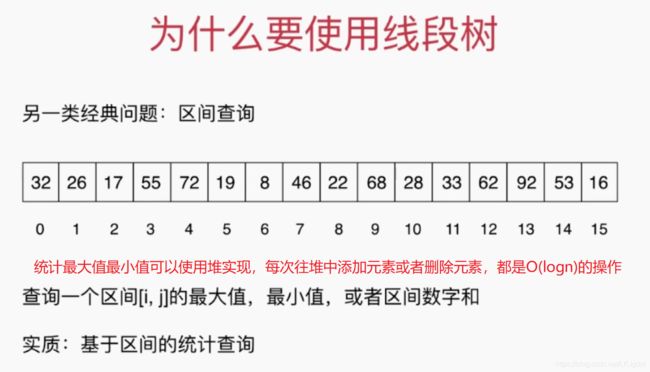
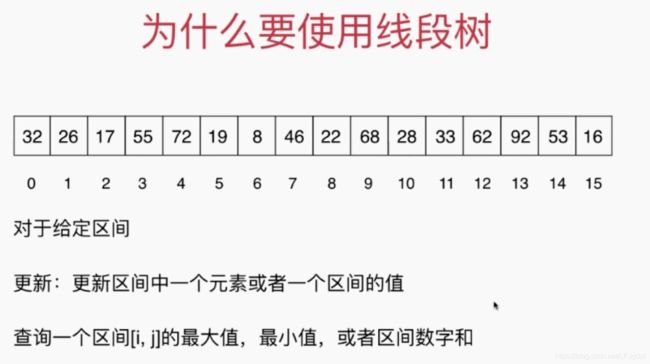
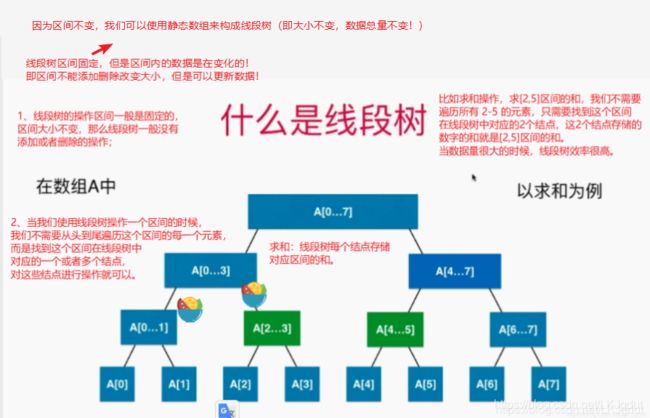
慕课网liuyubobobo老师课程学习笔记---part8：线段树

1、线段树介绍

2、线段树的基础表示

3、创建线段树、线段树区间查询

  线段树实现的代码如下：

package com.lkj;

public class SegmentTree<E>
{
     
    /*
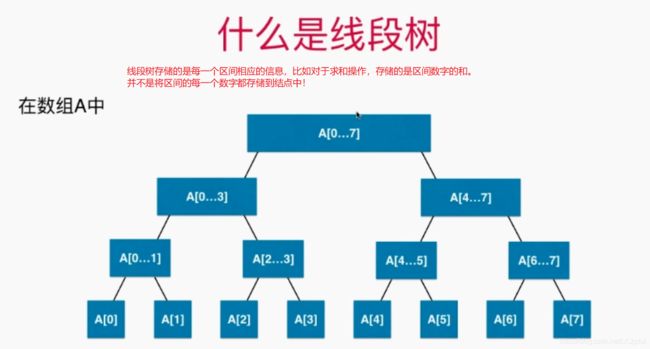
    使用一个数组表示区间.
    首先，用户可能要获取区间内某一个的元素，或者获取区间的某一个属性，我们在线段树中创建数组，作为区间数组的的副本，用于给出区间数组的某些属性；
    其次，我们想将data数组内的元素（arr数组区间传递进来的）组织成为一个线段树，那么还需要创建一个tree，大小为 4size
    */

    private E[] data;
    //tree结点虽然表示的是一个区间，但是它里面存储的实际上是区间内数据按一定方式计算得到的值。
    // 存储区间只是一种方式，目的还是得到区间内数字通过计算得到的值！
    private E[] tree;
    private Merger<E> merger;

    //初始化的时候传入一个区间数组
    public SegmentTree(E[] arr , Merger<E> merger)
    {
     
        this.merger = merger;

        data = (E[])new Object[arr.length];//使用arr初始化data
        for (int i = 0; i < arr.length ; i++)
        {
     
            data[i] = arr[i];
        }

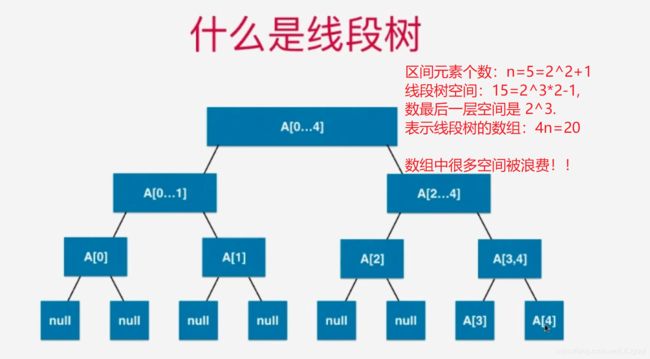
        tree = (E[])new Object[arr.length * 4];

        //调用 buildSegmentTree() 方法，完成线段树数组tree每一个结点 data数组区间的确定！
        //这样线段树一初始化，它的线段树数组中每一个结点所表示的 data数组的区间也确定了！
        buildSegmentTree(0 , 0 , data.length-1);//线段树从0位置开始赋予区间，此时区间为data最大区间：0-data.length-1
    }

    //线段树所关注的区间有多少个元素
    public int getSize()
    {
     
        return data.length;
    }

    public E get(int index)
    {
     
        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal.");
        return data[index];//数据可以获取区间数组的某一个下标的数据
    }

//---------------------------辅助函数：获取tree数组中某一下标的结点的左右孩子结点在数组的下标
    // 返回满二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
     
    return 2*index + 1;
}

    // 返回满二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
     
        return 2*index + 2;
    }

//--------------------------构建
    /**
     在treeIndex的位置创建表示区间[l...r]的线段树结点，即确定 线段树数组tree 在下标 treeIndex 位置所表示的 在data数组 中的区间。

     三个元素：1-要创建的线段树结点在tree数组中的索引；2，3-当前线段树结点表示的 data数组区间的左右端点的索引，注意这个索引是在data数组中的索引
     即在tree数组中，下标为 treeIndex，它在 data数组中表示的区间范围是： l-r

     这个方法设置为私有的，并且我们会从线段树数组 tree的0位置开始，不断确定线段树数组的每一个位置所表示的 data数组的区间，
     直到data数组区间的长度为1，此时遍历到线段树的叶子结点。这个过程中线段树数组可能有很多结点没有表示的区间！

     我们在线段树类的构造方法中就调用 buildSegmentTree() 方法，完成线段树数组每一个结点 data数组区间的确定！
     */
    private void buildSegmentTree(int treeIndex, int l, int r)
    {
     
        if(l == r)
        {
     
            //此时遍历到线段树的叶子结点，因为只有叶子结点表示的 data数组的区间长度为1，那么直接给叶子结点赋值为 data[l]
            tree[treeIndex] = data[l];
            //注意，到达叶子结点就return结束函数，否则下面继续计算，会导致出现大雨tree数组下标的子结点，出现数组下标越界
            return;
        }

        //下面我们继续给当前结点的左右孩子结点设置他们在 data数组中的区间

        //首先求左右孩子结点在tree数组中的下标
        int leftNodeIndex = leftChild(treeIndex);
        int rightNodeIndex = rightChild(treeIndex);

        //求区间中间的分割值
        // int mid = (l + r) / 2;//当l与r很大的时候，可能产生整形溢出的问题
        int mid = l + (r - l) / 2;

        //递归调用buildSegmentTree设置左右孩子结点在 data数组的区间
        buildSegmentTree(leftNodeIndex , l , mid);
        buildSegmentTree(rightNodeIndex , mid+1 , r);//这种设置方法，在区间长度为奇数的时候，左孩子结点区间比右孩子结点区间长度大1

        /**
         下面考虑 线段树tree treeIndex位置的值，这个值与我们的业务相关。
         我们综合当前结点左右孩子结点在data数组中的线段信息，就可以得到当前结点的线段信息！因为当前结点线段的区间，等于它左右孩子线段区间的和！

         我们创建一个融合接口，然后用户可以创建实现这个融合接口的类，自定义它融合左右孩子区间的含义，将这个自定义的对象传递进来，
         那么此时我们tree数组中 treeIndex 位置的值，就可以根据融合的规则，融合左右孩子结点的值得到！
         public interface Merger
         {
            E merge(E a , E b);
         }
         */
        tree[treeIndex] = merger.merge(tree[leftNodeIndex], tree[rightNodeIndex]);
    }

//---------------------------------------查询方法

    // 返回区间[queryL, queryR]的值，这个区间的值是由我们传入的Merger实现类定义的（可能是区间元素和，区间最大值等！）
    public E query(int queryL , int queryR)
    {
     
        //将参数不合理的情况排除
        if(queryL < 0 || queryL >= data.length ||
                queryR < 0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("Index is illegal.");

        return query(0 , 0 , data.length-1 , queryL , queryR);
    }

    /**
     * 在以treeIndex为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值，
     * 即对于线段树数组下标为 treeIndex 的结点，它在data数组的区间是 [l...r]，查询在 [l...r] 区间内 区间[queryL...queryR]的值
     *
     * 对于每一个 tree 数组结点，我们都传入它在 data数组中所表示的区间，我们其实可以将他们封装成为一个线段树的结点类，
     * 结点类包含当前线段树结点 在tree数组的下标:treeIndex，以及在data数组 区间的范围: [l,r]！
     * 理解：int treeIndex, int l, int r：这三个参数都在表示线段树结点的信息！！！
     */
    //我们向下将最开始的查询区间拆分，直到某一个小区间满足当前 tree结点的区间，我们直接将tree结点的值返回即可！
    private E query(int treeIndex, int l, int r, int queryL, int queryR)
    {
     
        //小区间满足当前 tree结点的区间，我们直接将tree结点的值返回即可！
        //当然，tree结点的值由其左右孩子结点区间值融合而来，这里我们在 buildSegmentTree() 方法中已经定义好！
        if(l == queryL && r == queryR)
            return tree[treeIndex];

        //如果当前tree结点的区间大于 查询的小区间 （小于的情况上面方法中被我们排除了！），查询tree结点左右孩子结点的区间

        //首先求左右孩子结点在tree数组中的下标
        int leftNodeIndex = leftChild(treeIndex);
        int rightNodeIndex = rightChild(treeIndex);

        //求当前tree结点分割为左右孩子区间的时候，区间中间的分割值：左区间：[l,mid]，右区间：[mid+1 , r]
        int mid = l + (r - l) / 2;

        if(queryL>=mid+1) //当查询的区间全部在右孩子结点的区间
            return query(rightNodeIndex , mid+1 , r , queryL , queryR);
        else if(queryR<=mid) //当查询的区间全部在左孩子结点的区间
            return query(leftNodeIndex , l , mid , queryL , queryR);

        //否则，我们得将查询区间分为2部分，分别在左右孩子区间查找
        E leftResult = query(leftNodeIndex , l , mid , queryL , mid);
        E rightResult = query(rightNodeIndex , mid+1 , r , mid+1 , queryR);

        //按用户定义的融合方法融合2个值并返回！
        return merger.merge(leftResult,rightResult);
    }


//----------------------toString方法
    @Override
    public String toString(){
     
        StringBuilder res = new StringBuilder();
        res.append('[');
        for(int i = 0 ; i < tree.length ; i ++){
     
            if(tree[i] != null)
                res.append(tree[i]);
            else
                res.append("null");

            if(i != tree.length - 1)
                res.append(", ");
        }
        res.append(']');
        return res.toString();
    }
}

4、LeetCode303题与307题：区域和检索 - 数组不可变、区域和检索 - 数组可修改
  303题目描述：给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

  代码不贴了，参考自己的源码！

  分析：注意，区间不可变，即作为查询区间的数组内的元素是不会变化的！
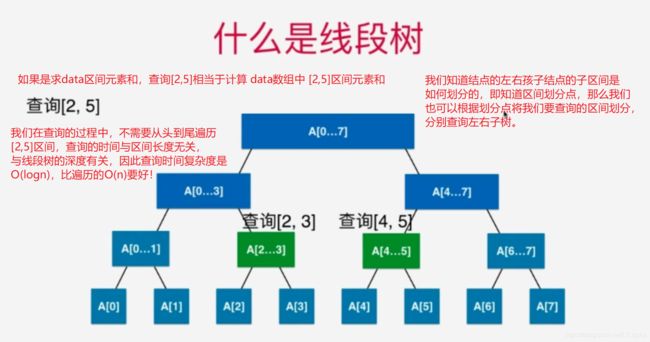
1）使用线段树：假设数组大小为n，被查询区间的总长度为数组长度n。我们使用线段树实现，查询区间 [ i , j ] 的时间复杂度是 ：O(logn)；
2）直接遍历：如果我们直接遍历查询区间 [ i , j ]，最坏情况是当查询区间 [ i , j ] 为整个数组时，那么查询的时间复杂度是：O(n)；
3）求和数组法：我们定义 sum[i]存储前i个元素和，在初始化的时候，通过 O(n) 的操作给 sum 数组赋值，随后我们在查询 区间 [ i , j ] 的时候，只需要用 sum[j+1] - sum[i] 即可，每一次查询操作都是 O(1) 的复杂度，在多次查询的情况下，这种方法的效率比使用线段树高！当然，这种方法只能在数组区间值无变化的时候使用，如果区间内元素值变化，则不可以使用这种方法！

  对于以上303题，由于区间的数据是固定的，而线段树主要用于区间内数据动态变化的情况，因此对于固定的区间，使用线段树反而比另外的方法效果差。我们看下面动态区间的例子。

  307题目描述：给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。
  如果我们仍然使用 求和数组法 ，update()方法更新的时候，需要重新改变求和数组 sum[] 内的值，虽然 sumRange 方法依然是O(1)，但是每一次更新都会花费O(n)的时间。
  在LeetCode运行的时候，出现超出时间限制的提示。 因为如果我们存在多次更新操作，就有多次 O(n) 的更新操作，这样导致算法的时间性能过差。
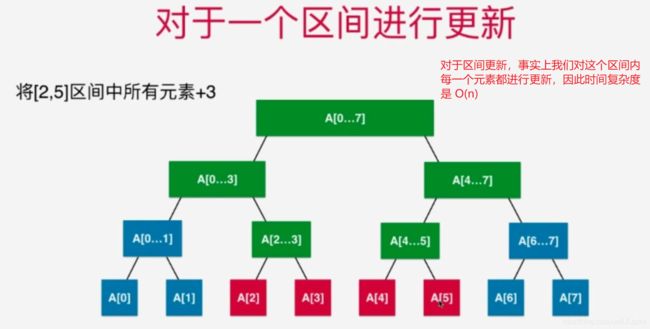
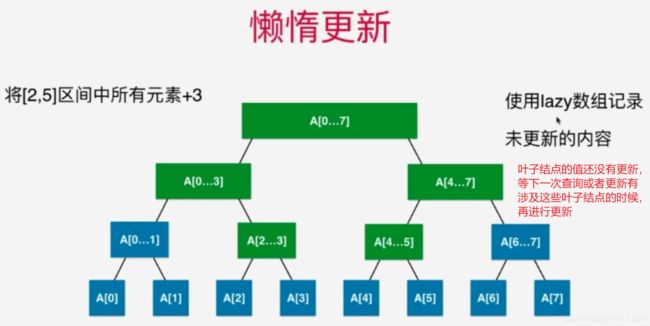
  那么此时我们使用线段树的方法，线段树构造的原理是：使用data数组构造线段树，线段树每个结点都代表data数组的一个区间。同时，定义线段树区间融合的方式。 此时data数组的数据更新，我们使用线段树的set()方法，堆线段树进行更新（更新线段树结点的区间内的值，实际上就是按照区间内值得变化，更新线段树结点的值！），这个更新方法的时间复杂度是 O(logn)。

求和数组法：初始化：O(n)、更新：O(n)、查询：O(1)
线段树：初始化：O(n)、更新：O(logn)、查询：O(logn)
当更新操作过多的时候，就会出现性能问题

  当我们操作的区间需要实现动态更新的时候，使用线段树比较好！

5、更多线段树相关话题