BEGAN: Boundary Equilibrium Generative Adversarial Networks阅读笔记

BEGAN: Boundary Equilibrium Generative Adversarial Networks阅读笔记

---

摘要

我们提出了一种新的用于促成训练时生成器和判别器实现均衡（Equilibrium）的方法，以及一个配套的 loss，这个 loss 由 Wasserstein distance 衍生而来，Wasserstein distance 则是训练基于自编码器的生成对抗网络（GAN）使用的。此外，这种新的方法还提供了一种新的近似收敛手段，实现了快速稳定的训练和很高的视觉质量。我们还推导出一种能够控制权衡图像多样性和视觉质量的方法。在论文里我们专注于图像生成任务，在更高的分辨率下建立了视觉质量的新里程碑。所有这些都是使用相对简单的模型架构和标准的训练流程实现的。

1.简介

谷歌公司的 Berthelot、Tom Schumm 和 Metz 本周发表论文 BEGAN（Boundary Equilibrium GAN），提出了“边界均衡 GAN” 的概念，借鉴了 EBGAN 和 WGAN 各自的优点，使用简单的模型，在标准的训练步骤下取得了令人惊艳的效果。不仅如此，论文还提出了一个可以衡量收敛的超参数，实现了快速稳定的训练和很高的视觉质量。

作者在论文中写道，他们的主要贡献是：

一个简单且且强壮的 GAN 架构，使用标准的训练步骤实现了快速、稳定的收敛。

一种均衡的概念，用于平衡判别器和生成器（判别器往往在训练早期就以压倒性优势胜过生成器），通过参数 k 实现。

一种控制在图像多样性与视觉质量之间权衡的新方法,通过超参数γ实现。

用于近似衡量收敛的方法实现by Convergence measure Mglobal ，据我们所知，目前发表过的这类方法另外只有一种，那就是 Wasserstein GAN。

1.2EBGAN

“EBGAN 是 Yann LeCun 课题组提交到 ICLR2017的一个工作，从能量模型的角度对 GAN 进行了扩展。EBGAN 将判别器看做是一个能量函数，这个能量函数在真实数据域附近的区域中能量值会比较小，而在其他区域（即非真实数据域区域）都拥有较高能量值。因此，EBGAN 中给予 GAN 一种能量模型的解释，即生成器是以产生能量最小的样本为目的，而判别器则以对这些产生的样本赋予较高的能量为目的。

“从能量模型的角度来看待判别器和 GAN 的好处是，我们可以用更多更宽泛的结构和损失函数来训练 GAN 结构，比如文中就用自编码器（AE）的结构来作为判别器实现整体的GAN 框架，如下图所示：

在训练过程中，EBGAN 比 GAN 展示出了更稳定的性能，也产生出了更加清晰的图像。

2.Proposed method（提出的方法）

我们的方法使用从 Wasserstein 距离衍生而来的 loss 去匹配自编码 loss 分布。这是使用经典的GAN模型目标加上一个平衡项以平衡鉴别器和生成器。 我们的方法训练过程和网络架构较之GAN更加简单。

2.1Wasserstein距离下限为自动编码器

我们希望研究重构误差分布，而不是重构样本的分布。 我们首先介绍自编码器的loss，然后我们计算真实样本和生成样本的自编码loss 分布之间的Wasserstein距离的边界值。

loss采用pixel level的L1或者L2 norm，即

L(v)=∥v−D(v)∥p ,p∈1,2

接下来用 μ1,2 来分别表示真实样本的loss分布和生成样本的loss分布， Γ(μ1,μ2) 为其联合分布，
m1,2 表示各自的均值，那么Wasserstein 距离就用来确定这两个loss 分布的距离，表示为：

W(μ1,μ2)=infγ∼Γ(μ1,mu2)E(x1,x2)∼γ[||x1−x2||]

由Jensen不等式得：

infE[||x1−x2||]⩾inf||E[x1−x2]||=||m1−m2||

2.2GAN目标

根据GAN对抗性的原则，D的目标是拉大两个分布的距离，也就是最大化 W(μ1,μ2) ，而G的目标则是拉近两个分布的距离。

由于 m1,m2∈R+ ，最大化 W(μ1,μ2 )实际上有两组解：

W(μ1,μ2)=m1−m2,m1→∞,m2→0W(μ1,μ2)=m2−m1,m1→0,m2→∞

根据D和G的目标，不难确定第二组解更合理。它一方面拉大两个分布的距离，另一方面还能降低真实样本的重构误差（ m1 代表真实样本重构误差，越小越好）。而G 为了缩小两个分布的差异，可以通过最小化 m2 来实现。也就是说（D实际上已对目标函数取了相反数，因此下面两个目标函数都需要最小化）

minDLD=L(x;θD)−\L(G(zD;θG);θD)minGLG=−LD

2.3均衡概念提出

当生成器的loss和鉴别器的loss满足下式时认为两者均衡，此时鉴别器分辨出真假样本的概率是相同的。

E[L(x)]=E[L(G(z))]

然而，当D和G的能力不相当时，一方很容易就打败了另一方，这将导致训练不稳定。为此，作者引入了一个超参数 γ∈[0,1] 来平衡两者的loss：

γ=Ez(L(G(z)))Ex(L(x))

在我们的模型里，鉴别器有两个竞争的目标：对真实图像自编码和从生成的图像中区别出真正的图像。

当 γ 较小时，D致力于最小化真实样本的重构误差，相对来说，而对生成样本的关注较少（此处有疑问），这将导致生成样本的多样性降低。作者称这个超参数为diversity ratio，它控制生成样本的多样性。

所以现在的目标有两个，尽可能地最小化GAN object以及尽可能地满足保证公式(8)成立。综合这两个目标，可以设计一个判断收敛情况的指标，使用均衡概念推导出一个全局的收敛度量：我们可以构建收敛过程通过找到最接近的重建值 L（x） 加上比例控制算法的瞬时过程误差的绝对值 |γL(x)−L(G(z))| 。

M=L(x)+|γL(x)−L(G(z))|

为了尽可能地满足公式\mathbb{E}[\mathcal{L}(x)]=\mathbb{E}[\mathcal{L}(G(z))] ，作者借鉴控制论中的“比例控制理论”(Proportional Control Theory)，引入比例增益 λk 和比例控制器的输出 kt ，完整的BEGAN的目标函数如下：

LDLGkt+1=L(x)−ktL(G(z)),for θD=L(G(z)),for θG=kt+λk(γL(x)−L(G(z))),for each training step t

我们用比例控制理论来实现 γE[L(x)]=E[L(G(z))] 。
这个等式由 kt∈[0,1] 来控制 L(G(z)) 在梯度下降时的比例实现。 k0=0 , λk 是 k 的比例增益，也即是 k 的学习率， λk=0.001
实质上，这可以被认为是一种的闭环反馈控制，在每一步骤调整 kt 以维持方程式 γE[L(x)]=E[L(G(z))] ,优化器选择Adam。

在早期训练阶段，因为生成的数据接近0，并且实际数据分布尚未被准确地学习，G容易为自编码器生成易于重建的数据。
这样就有 L(x)>L(G(z)) (???)，并通过均衡约束在整个训练过程成立。

3.实验

代码为tensorpack/examples/GAN/BEGAN.py\
数据集为celebA/Align\&Cropped images\
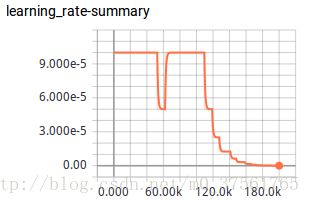
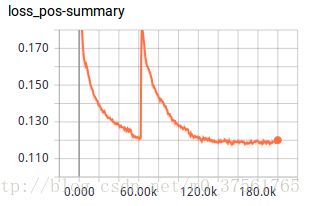
代码还没有看，先跑了一下结果。

下节分析论文实验部分和代码。