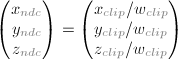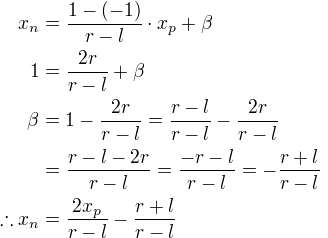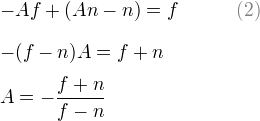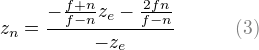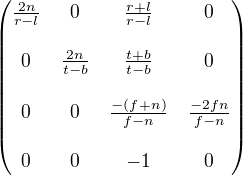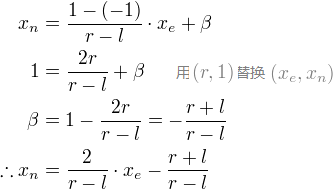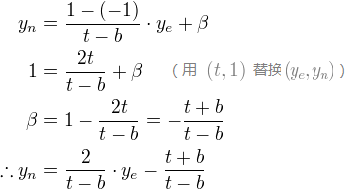投影矩阵的推导(OpenGl)

概述

计算机显示器是一个2D平面。OpenGL渲染的3D场景必须以2D图像方式投影到计算机屏幕上。GL_PROJECTION矩阵用于该投影变换。首先，它将所有定点数据从观察坐标转换到裁减坐标。接着，这些裁减坐标通过除以w分量的方式转换到归一化设备坐标（NDC）。

因此，我们需要记住一点：裁减变换（视锥剔除）与NDC变换都保存在GL_PROJECTION矩阵中。下述章节描述如何从6个限定参数（左、右、下、上、近平面、远平面）构建投影矩阵。

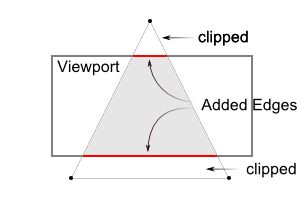
注意，视锥剔除（裁减）在裁减坐标上执行，并且在除以w_c之前。裁减坐标x_c、y_c、z_c会与w_c做比较检测。如果任一坐标小于-w_c或大于w_c，则该顶点将会抛弃。

接着，OpenGL重新构建那些裁减掉的多边形的边。

 
被视锥裁减的三角形

---

透视投影

 
OpenGL透视视锥体与NDC

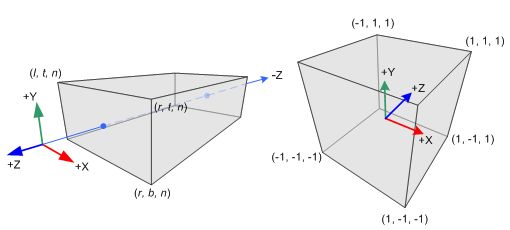
在透视投影中，截棱锥体（观察坐标）中的3D点会被映射到立方体（NDC）中。x坐标的范围从[l,f]到[-1,1]，y坐标的范围从[b,t]到[-1,1]，z坐标的范围从[n,f]到[-1,1]。

注意，观察坐标为右手坐标系，NDC使用左右坐标系。也就是说，位于原点的照相机在观察坐标中看向-Z轴，而在NDC中看向+Z轴。因为glFrustum()只接收正的近平面与远平面距离值，我们需要在构建GL_PROJECTION矩阵时对他们取反。

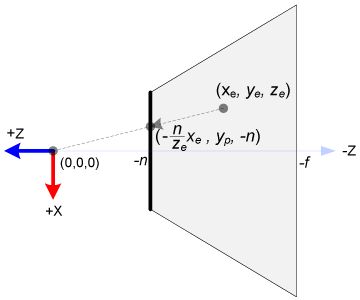
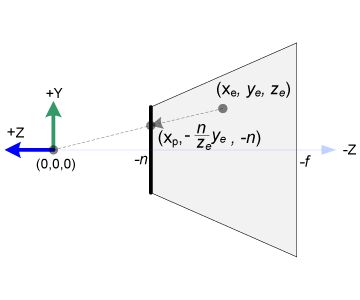
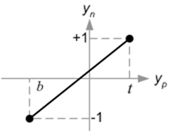
OpenGL中，观察空间中的3D点被投影到近平面（投影平面）上。下图展示观察空间中的点(x_e,y_e,z_e)如何投影到近平面上的点(x_p,y_p,z_p)。

 
视锥体的俯视图

 
视锥体的侧视图

 

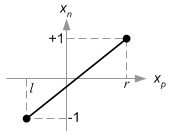
从视锥体的俯视图看出，使用相似三角形比率计算方式将观察空间的x坐标x_e被映射到x_p。

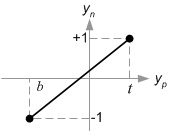
从视锥体的侧视图看出，y_p也使用相同的方式计算出：

注意，x_p与y_p二者都依赖于z_e，它们与-z_e成反比例。也就是说，它们都被-z_e除。这是构建GL_PROJECTION矩阵的第一点提示。在观察坐标通过与GL_PROJECTION矩阵相乘变换之后，裁减坐标依旧是其次坐标。它最终通过除以裁减坐标的w分量才变成归一化设备坐标（NDC）。（更详细描述参考OpenGL变换。）

, 

因此，我们可以将裁减坐标的w分量设置为-z_e。这样，GL_PROJECTION矩阵的第四行变为(0,0,-1,0)。

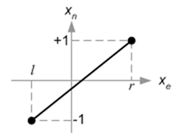
接着，我们通过线性关系将x_p与y_p映射到NDC中的x_n与y_n：[l,r]=>[-1,1]，[b,t]=>[-1,1]。

映射x_p到x_n

 

映射y_p到y_n

然后,我们用上面的方程式替换x_p与y_p。

    

注意，我们为透视除法（x_c/w_c, y_c/w_c）将每个等式相被-z_e整除。前面我们已经将w_c设置为-z_e，大括号中的项为裁减坐标中x_c与y_c。

从这个等式，我们可以发现GL_PROJECTION矩阵的第一与第二行。

现在，我们仅仅解决GL_PROJECTION矩阵的3行。由于观察空间中的z_e总是投影到近平面上的-n点，z_n的计算方法与其他坐标的计算方法有稍许不同。不过我们需要唯一的z值来进行裁剪与深度测试。此外，我们也会进行逆投影（逆变换）操作。因为，我们知道z并不依赖于x与y的值，我们借助w分量找寻z_n与z_e之间的关系。因此，我们可以像这样指定GL_PROJECTION矩阵的第三行：

在观察空间，we等于1。因此，等式变为：

为了计算系数A与B，我们使用(ze,zn)关系式(-n,-1)与(-f,1)，且将它们带入到上述等式。

为了求解A与B，重写等式(1)：

将等式(1')带入等式(2)，然后求解A：

将A带入等式(1)中，求出B：

我们解出A与B。因此z_e与z_n的关系变为：

最后，我们解出GL_PROJECTION矩阵的所有元素。完整的投影矩阵为：

   OpenGL透视投影矩阵

该投影矩阵为通用截面体。如果视锥体为对称的，即r=-l且t=-b，则矩阵可简化为：

在开始后面讲述之前，请回顾z_e与z_n之间的关系：等式(3)。你会注意到它是一个有理数方程且z_e与z_n并非线性关系。也就是说近平面具有非常高的精度，而远平面的精度很低。如果[-n,-f]的范围变得很大，会引起深度精度问题（深度冲突）：远平面附近z_e的小变化不会影响z_n值。为了最小化深度缓存精度问题，n与f的距离应该尽可能小。

深度缓存精度比较

---

正交投影

 
正交椎体与归一化设备坐标（NDC）

构造正交投影的GL_PROJECTION矩阵比透视投影模式简单很多。

观察空间的x_e、y_e与z_e分量都线性映射到NDC。我们只需将长方体缩放为正方体，然后移动它到原点。让我们使用线性关系推导出GL_PROJECTION中的所有元素。

映射x_e到x_n

 

映射y_e到y_n

 

 
映射z_e到z_n

因为对于正交投影并不需要w分量，GL_PROJECTION矩阵的第4行依旧为(0,0,0,1)。因此，正交投影完整的GL_PROJECTION矩阵为：

OpenGL正交投影矩阵

如果视锥体是对称的（r=-l且t=-b），它可以进一步简化。

 

英文原文：http://www.songho.ca/opengl/gl_projectionmatrix.html