排列组合十一个性质公式及证明,错排数公式及证明
文章目录
- 排列数
- 组合数
- 求组合数常用公式
-
- 定义式
- 递推式
- 杨辉三角
- 组合数常用性质及证明
-
- 性质一
- 性质二
- 性质三
- 性质四(二项式定理)
- 性质五
- 性质六
- 性质七
- 性质八
- 性质九
- 性质十
- 性质十一
- 错排数
排列数
从 n n n个物品中不放回地依次选 m m m个物品,考虑顺序,有多少种方案,记作 A n m A_n^m Anm
A n m = n ! ( n − m ) ! A_n^m=\frac{n!}{(n-m)!} Anm=(n−m)!n!
组合数
从 n n n个物品中不放回地依次选 m m m个物品,不考虑顺序,有多少种方案,记作 C n m C_n^m Cnm
C n m = n ! m ! ∗ ( n − m ) ! C_n^m=\frac{n!}{m!*(n-m)!} Cnm=m!∗(n−m)!n!
求组合数常用公式
定义式
C n m = n ! m ! ∗ ( n − m ) ! C_n^m=\frac{n!}{m!*(n-m)!} Cnm=m!∗(n−m)!n!
当 n , m n,m n,m很大时,预处理阶乘和逆元,预处理 O ( n ) O(n) O(n),求组合数 O ( 1 ) O(1) O(1)
递推式
C n m = n ! m ! ∗ ( n − m ) ! = n ! ( m − 1 ) ! ∗ ( n − m + 1 ) ! ∗ n − m + 1 m = C n m − 1 ∗ n − m + 1 m C_n^m=\frac{n!}{m!*(n-m)!}=\frac{n!}{(m-1)!*(n-m+1)!}*\frac{n-m+1}{m}=C_n^{m-1}*\frac{n-m+1}{m} Cnm=m!∗(n−m)!n!=(m−1)!∗(n−m+1)!n!∗mn−m+1=Cnm−1∗mn−m+1
杨辉三角
C n m = n ! m ! ∗ ( n − m ) ! = ( n − 1 ) ! ∗ ( n − m + m ) m ! ∗ ( n − m ) ! C_n^m=\frac{n!}{m!*(n-m)!}=\frac{(n-1)!*(n-m+m)}{m!*(n-m)!} Cnm=m!∗(n−m)!n!=m!∗(n−m)!(n−1)!∗(n−m+m)
= ( n − 1 ) ! ∗ ( n − m ) m ! ∗ ( n − m ) ! + ( n − 1 ) ! ∗ m m ! ∗ ( n − m ) ! =\frac{(n-1)!*(n-m)}{m!*(n-m)!}+\frac{(n-1)!*m}{m!*(n-m)!} =m!∗(n−m)!(n−1)!∗(n−m)+m!∗(n−m)!(n−1)!∗m
= ( n − 1 ) ! m ! ∗ ( n − m − 1 ) ! + ( n − 1 ) ! ( m − 1 ) ! ∗ ( n − m ) ! =\frac{(n-1)!}{m!*(n-m-1)!}+\frac{(n-1)!}{(m-1)!*(n-m)!} =m!∗(n−m−1)!(n−1)!+(m−1)!∗(n−m)!(n−1)!
= C n − 1 m + C n − 1 m − 1 =C_{n-1}^m+C_{n-1}^{m-1} =Cn−1m+Cn−1m−1
当模数不是质数的时候,预处理 O ( n 2 ) O(n^2) O(n2),求组合数 O ( 1 ) O(1) O(1)
组合数常用性质及证明
性质一
C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m
证明:
法一:利用组合数意义理解
在 n n n个当中选 m m m个,相当于在 n n n个当中不选 n − m n-m n−m个
法二:公式表示
C n m = n ! m ! ∗ ( n − m ) ! C_n^m=\frac{n!}{m!*(n-m)!} Cnm=m!∗(n−m)!n!
C n n − m = n ! ( n − m ) ! ∗ ( n − ( n − m ) ) ! = n ! m ! ∗ ( n − m ) ! C_n^{n-m}=\frac{n!}{(n-m)!*(n-(n-m))!}=\frac{n!}{m!*(n-m)!} Cnn−m=(n−m)!∗(n−(n−m))!n!=m!∗(n−m)!n!
性质二
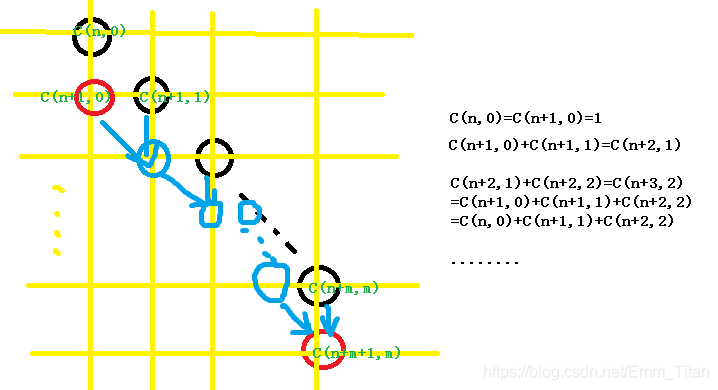
C n + m + 1 m = ∑ i = 0 m C n + i i C_{n+m+1}^m=\sum_{i=0}^mC_{n+i}^i Cn+m+1m=i=0∑mCn+ii
性质三
C n m ∗ C m r = C n r = C n − r m − r C_n^m*C_m^r=C_n^r=C_{n-r}^{m-r} Cnm∗Cmr=Cnr=Cn−rm−r
证明:
法一:利用组合数意义理解
在 n n n个当中选 m m m个,再在选出的 m m m个当中选 r r r个
相当于在 n n n个当中选 r r r个,再在剩下的 n − r n-r n−r个中选还需要的 m − r m-r m−r
法二:公式推导
C n m ∗ C m r = n ! m ! ∗ ( n − m ) ! ∗ m ! r ! ∗ ( m − r ) ! = n ! ∗ m ! m ! ∗ r ! ∗ ( n − m ) ! ∗ ( m − r ) ! C_n^m*C_m^r=\frac{n!}{m!*(n-m)!}*\frac{m!}{r!*(m-r)!}=\frac{n!*m!}{m!*r!*(n-m)!*(m-r)!} Cnm∗Cmr=m!∗(n−m)!n!∗r!∗(m−r)!m!=m!∗r!∗(n−m)!∗(m−r)!n!∗m! = n ! r ! ∗ ( n − m ) ! ∗ ( m − r ) ! = n ! ∗ ( n − r ) ! r ! ∗ ( n − m ) ! ∗ ( m − r ) ! ∗ ( n − r ) ! =\frac{n!}{r!*(n-m)!*(m-r)!}=\frac{n!*(n-r)!}{r!*(n-m)!*(m-r)!*(n-r)!} =r!∗(n−m)!∗(m−r)!n!=r!∗(n−m)!∗(m−r)!∗(n−r)!n!∗(n−r)! = n ! r ! ∗ ( n − r ) ! ∗ ( n − r ) ! ( m − r ! ) ∗ ( n − m ) ! { ( n − r ) − ( m − r ) = n − m } =\frac{n!}{r!*(n-r)!}*\frac{(n-r)!}{(m-r!)*(n-m)!}\ \ \ \ \ \{(n-r)-(m-r)=n-m\} =r!∗(n−r)!n!∗(m−r!)∗(n−m)!(n−r)! { (n−r)−(m−r)=n−m} = C n r ∗ C n − r m − r =C_n^r*C_{n-r}^{m-r} =Cnr∗Cn−rm−r
性质四(二项式定理)
∑ i = 0 n { C n i ∗ x i } = ( 1 + x ) n \sum_{i=0}^n\{C_n^i*x^i\}=(1+x)^n i=0∑n{ Cni∗xi}=(1+x)n
∑ i = 0 n C n i = 2 n ( x = 1 ) \sum_{i=0}^nC_n^i=2^n\ \ \ (x=1) i=0∑nCni=2n (x=1)
( 1 + x ) n = ( 1 + x ) ∗ ( 1 + x ) ∗ . . . ∗ ( 1 + x ) (1+x)^n=(1+x)*(1+x)*...*(1+x) (1+x)n=(1+x)∗(1+x)∗...∗(1+x), n n n个 ( 1 + x ) (1+x) (1+x)相乘
( 1 + x ) (1+x) (1+x)在乘法中的贡献相当于要么选 1 1 1,要么选 x x x
有 i i i个 ( 1 + x ) (1+x) (1+x)中选 x x x,产生的贡献就是 x i x^i xi,剩下的 n − i n-i n−i个 ( 1 + x ) (1+x) (1+x),产生的贡献是 1 1 1
在 n n n个中任意选 i i i个,相当于 C n i C_n^i Cni
性质五
∑ i = 0 n { ( − 1 ) i ∗ C n i } = 0 \sum_{i=0}^n\{(-1)^i*C_n^i\}=0 i=0∑n{ (−1)i∗Cni}=0
证明:
①:若 n n n为奇数
则 ∑ i = 0 n \sum_{i=0}^n ∑i=0n共有 n + 1 n+1 n+1项(偶数项),而 ( − 1 ) i ∗ C n i = ( − 1 ) i ∗ C n n − i (-1)^i*C_n^i=(-1)^i*C_n^{n-i} (−1)i∗Cni=(−1)i∗Cnn−i
因为 n n n为奇数,所以当 i i i为奇数时, n − i n-i n−i为偶数,当 i i i为偶数时, n − i n-i n−i为奇数
所以 i , n − i i,n-i i,n−i奇偶性不同,那么 ( − 1 ) i + ( − 1 ) n − 1 (-1)^i+(-1)^{n-1} (−1)i+(−1)n−1相当于 ( − 1 ) 奇 数 次 方 + ( − 1 ) 偶 数 次 方 = 0 (-1)^{奇数次方}+(-1)^{偶数次方}=0 (−1)奇数次方+(−1)偶数次方=0
( − 1 ) i ∗ C n i + ( − 1 ) n − i ∗ C n n − i = 0 (-1)^i*C_n^i+(-1)^{n-i}*C_n^{n-i}=0 (−1)i∗Cni+(−1)n−i∗Cnn−i=0
偶数项刚好每一对可以相互抵消,所以性质显然成立
②:若 n n n为偶数
( − 1 ) 0 = ( − 1 ) n = 1 (-1)^0=(-1)^n=1 (−1)0=(−1)n=1,先把 i = 0 , i = n i=0,i=n i=0,i=n的情况拆出来,用杨辉三角展开中间项
∑ i = 0 n { ( − 1 ) i ∗ C n i } = C n 0 + C n n + ∑ i = 1 n − 1 { ( − 1 ) i ∗ ( C n − 1 i + C n − 1 i − 1 ) } \sum_{i=0}^n\{(-1)^i*C_n^i\}=C_n^0+C_n^n+\sum_{i=1}^{n-1}\{(-1)^i*(C_{n-1}^i+C_{n-1}^{i-1})\} i=0∑n{ (−1)i∗Cni}=Cn0+Cnn+i=1∑n−1{ (−1)i∗(Cn−1i+Cn−1i−1)}
C n 0 + C n n + ∑ i = 0 n − 2 { ( − 1 ) i + 1 ∗ C n − 1 i } + ∑ i = 1 n − 1 { ( − 1 ) i ∗ C n − 1 i } C_n^0+C_n^n+\sum_{i=0}^{n-2}\{(-1)^{i+1}*C_{n-1}^i\}+\sum_{i=1}^{n-1}\{(-1)^i*C_{n-1}^i\} Cn0+Cnn+i=0∑n−2{ (−1)i+1∗Cn−1i}+i=1∑n−1{ (−1)i∗Cn−1i}
把前一个求和加上 ( − 1 ) n ∗ C n − 1 n − 1 (-1)^n*C_{n-1}^{n-1} (−1)n∗Cn−1n−1一项,后一个求和加上 ( − 1 ) 0 ∗ C n − 1 0 (-1)^0*C_{n-1}^0 (−1)0∗Cn−10

C n 0 + C n n + ∑ i = 0 n − 1 { ( − 1 ) i ∗ C n − 1 i } − C n − 1 n − 1 + ∑ i = 1 n − 1 { ( − 1 ) i ∗ C n − 1 i } − C n − 1 0 C_n^0+C_n^n+\sum_{i=0}^{n-1}\{(-1)^i*C_{n-1}^i\}-C_{n-1}^{n-1}+\sum_{i=1}^{n-1}\{(-1)^i*C_{n-1}^i\}-C_{n-1}^0 Cn0+Cnn+i=0∑n−1{ (−1)i∗Cn−1i}−Cn−1n−1+i=1∑n−1{ (−1)i∗Cn−1i}−Cn−10
注意 n − 1 n-1 n−1为奇数,奇数情况已经证明了,故这两个公式直接等于 0 0 0,删掉,原式转化为
C n 0 + C n n − C n − 1 0 − C n − 1 n − 1 = 0 C_n^0+C_n^n-C_{n-1}^0-C_{n-1}^{n-1}=0 Cn0+Cnn−Cn−10−Cn−1n−1=0
性质六
C n 0 + C n 2 + . . . = C n 1 + C n 3 + . . . = 2 n − 1 C_n^0+C_n^2+...=C_n^1+C_n^3+...=2^{n-1} Cn0+Cn2+...=Cn1+Cn3+...=2n−1
证明:
用杨辉三角公式暴力展开寻找规律
①假设 n n n为奇数
C n 0 + C n 2 + . . . + C n n − 1 = C n − 1 0 + C n − 1 1 + C n − 1 2 + C n − 1 3 + C n − 1 4 + . . . + C n − 1 n − 2 + C n − 1 n − 1 C_n^0+C_n^2+...+C_n^{n-1}=C_{n-1}^0+C_{n-1}^1+C_{n-1}^2+C_{n-1}^3+C_{n-1}^4+...+C_{n-1}^{n-2}+C_{n-1}^{n-1} Cn0+Cn2+...+Cnn−1=Cn−10+Cn−11+Cn−12+Cn−13+Cn−14+...+Cn−1n−2+Cn−1n−1
C n 1 + C n 3 + . . . + C n n = C n − 1 0 + C n − 1 1 + C n − 1 2 + C n − 1 3 + . . . + C n − 1 n − 1 + C n − 1 n C_n^1+C_n^3+...+C_n^n=C_{n-1}^0+C_{n-1}^1+C_{n-1}^2+C_{n-1}^3+...+C_{n-1}^{n-1}+C_{n-1}^n Cn1+Cn3+...+Cnn=Cn−10+Cn−11+Cn−12+Cn−13+...+Cn−1n−1+Cn−1n
发现每一项都是相等的,第二个式子多出来的 C n − 1 n = 0 C_{n-1}^n=0 Cn−1n=0,所以相等得证
又根据性质四 ∑ i = 0 n C n i = 2 n \sum_{i=0}^nC_n^i=2^n ∑i=0nCni=2n,前两个式子相加刚好等于 ∑ i = 0 n C n i \sum_{i=0}^nC_n^i ∑i=0nCni,又相等, / 2 /2 /2即为 2 n − 1 2^{n-1} 2n−1

②假设 n n n为偶数
C n 0 + C n 2 + . . . + C n n = C n − 1 0 + C n − 1 1 + C n − 1 2 + C n − 1 3 + C n − 1 4 + . . . + C n − 1 n − 1 + C n − 1 n C_n^0+C_n^2+...+C_n^n=C_{n-1}^0+C_{n-1}^1+C_{n-1}^2+C_{n-1}^3+C_{n-1}^4+...+C_{n-1}^{n-1}+C_{n-1}^{n} Cn0+Cn2+...+Cnn=Cn−10+Cn−11+Cn−12+Cn−13+Cn−14+...+Cn−1n−1+Cn−1n
C n 1 + C n 3 + . . . + C n n − 1 = C n − 1 0 + C n − 1 1 + C n − 1 2 + C n − 1 3 + . . . + C n − 1 n − 2 + C n − 1 n − 1 C_n^1+C_n^3+...+C_n^{n-1}=C_{n-1}^0+C_{n-1}^1+C_{n-1}^2+C_{n-1}^3+...+C_{n-1}^{n-2}+C_{n-1}^{n-1} Cn1+Cn3+...+Cnn−1=Cn−10+Cn−11+Cn−12+Cn−13+...+Cn−1n−2+Cn−1n−1
仍然两两对应相等,第一个式子多出来的 C n − 1 n = 0 C_{n-1}^n=0 Cn−1n=0,后面的方法与奇数情况一样,不赘述
性质七
C n + m r = ∑ i = 0 m i n ( n , m , r ) { C n i ∗ C m r − i } C_{n+m}^r=\sum_{i=0}^{min(n,m,r)}\{C_n^i*C_m^{r-i}\} Cn+mr=i=0∑min(n,m,r){ Cni∗Cmr−i}
C n + m n = C n + m m = ∑ i = 0 m i n ( n , m ) { C n i ∗ C m i } , ( r = n ∣ ∣ r = m ) C_{n+m}^n=C_{n+m}^m=\sum_{i=0}^{min(n,m)}\{C_n^i*C_m^i\},(r=n||r=m) Cn+mn=Cn+mm=i=0∑min(n,m){ Cni∗Cmi},(r=n∣∣r=m)
证明:
用组合数意义理解
把 n + m n+m n+m个分成 n n n个一组, m m m个一组,总共选 r r r个,相当于 n n n个中选 i i i个, m m m个中选 r − i r-i r−i个
性质八
m ∗ C n m = n ∗ C n − 1 m − 1 m*C_n^m=n*C_{n-1}^{m-1} m∗Cnm=n∗Cn−1m−1
证明:
m ∗ C n m = m ∗ n ! m ! ∗ ( n − m ) ! = n ∗ ( n − 1 ) ! ( m − 1 ) ! ∗ ( n − m ) = n ∗ C n − 1 m − 1 m*C_n^m=m*\frac{n!}{m!*(n-m)!}=n*\frac{(n-1)!}{(m-1)!*(n-m)}=n*C_{n-1}^{m-1} m∗Cnm=m∗m!∗(n−m)!n!=n∗(m−1)!∗(n−m)(n−1)!=n∗Cn−1m−1
性质九
∑ i = 0 n { C n i ∗ i } = n ∗ 2 n − 1 \sum_{i=0}^n\{C_n^i*i\}=n*2^{n-1} i=0∑n{ Cni∗i}=n∗2n−1
证明:
∑ i = 0 n { C n i ∗ i } = ∑ i = 1 n { n ! i ! ∗ ( n − i ) ! ∗ i } = ∑ i = 1 n n ! ( i − 1 ) ! ∗ ( n − i ) ! \sum_{i=0}^n\{C_n^i*i\}=\sum_{i=1}^n\{\frac{n!}{i!*(n-i)!}*i\}=\sum_{i=1}^n\frac{n!}{(i-1)!*(n-i)!} i=0∑n{ Cni∗i}=i=1∑n{ i!∗(n−i)!n!∗i}=i=1∑n(i−1)!∗(n−i)!n! = ∑ i = 1 n { n ∗ ( n − 1 ) ! ( i − 1 ) ! ∗ ( n − i ) ! } = n ∗ ∑ i = 1 n C n − 1 i − 1 = n ∗ ∑ i = 0 n − 1 C n − 1 i = n ∗ 2 n − 1 =\sum_{i=1}^n\{n*\frac{(n-1)!}{(i-1)!*(n-i)!}\}=n*\sum_{i=1}^nC_{n-1}^{i-1}=n*\sum_{i=0}^{n-1}C_{n-1}^i=n*2^{n-1} =i=1∑n{ n∗(i−1)!∗(n−i)!(n−1)!}=n∗i=1∑nCn−1i−1=n∗i=0∑n−1Cn−1i=n∗2n−1

由性质四可知, ∑ i = 0 n C n i = 2 n , ∑ i = 0 n − 1 C n − 1 i = 2 n − 1 \sum_{i=0}^nC_n^i=2^n,\sum_{i=0}^{n-1}C_{n-1}^i=2^{n-1} ∑i=0nCni=2n,∑i=0n−1Cn−1i=2n−1
性质十
∑ i = 0 n { C n i ∗ i 2 } = n ∗ ( n + 1 ) ∗ 2 n − 2 \sum_{i=0}^n\{C_n^i*i^2\}=n*(n+1)*2^{n-2} i=0∑n{ Cni∗i2}=n∗(n+1)∗2n−2
证明:
利用性质九
∑ i = 0 n { C n i ∗ i 2 } = ∑ i = 0 n { n ! i ! ∗ ( n − i ) ! ∗ i ∗ ( i − 1 + 1 ) } \sum_{i=0}^n\{C_n^i*i^2\}=\sum_{i=0}^n\{\frac{n!}{i!*(n-i)!}*i*(i-1+1)\} i=0∑n{ Cni∗i2}=i=0∑n{ i!∗(n−i)!n!∗i∗(i−1+1)} = ∑ i = 0 n { n ! i ! ∗ ( n − i ) ! ∗ i + n ! i ! ∗ ( n − i ) ! ∗ i ∗ ( i − 1 ) } =\sum_{i=0}^n\{\frac{n!}{i!*(n-i)!}*i+\frac{n!}{i!*(n-i)!}*i*(i-1)\} =i=0∑n{ i!∗(n−i)!n!∗i+i!∗(n−i)!n!∗i∗(i−1)} = ∑ i = 0 n { C n i ∗ i } + ∑ i = 1 n { n ! ( i − 1 ) ! ∗ ( n − i ) ! ∗ ( i − 1 ) } =\sum_{i=0}^n\{C_n^i*i\}+\sum_{i=1}^n\{\frac{n!}{(i-1)!*(n-i)!}*(i-1)\} =i=0∑n{ Cni∗i}+i=1∑n{ (i−1)!∗(n−i)!n!∗(i−1)} = n ∗ 2 n − 1 + n ∗ ∑ i = 1 n { ( n − 1 ) ! ( i − 1 ) ! ∗ ( n − i ) ! ∗ ( i − 1 ) } =n*2^{n-1}+n*\sum_{i=1}^n\{\frac{(n-1)!}{(i-1)!*(n-i)!}*(i-1)\} =n∗2n−1+n∗i=1∑n{ (i−1)!∗(n−i)!(n−1)!∗(i−1)} = n ∗ 2 n − 1 + n ∗ ∑ i = 1 n { C n − 1 i − 1 ∗ ( i − 1 ) } = n ∗ 2 n − 1 + n ∗ ∑ i = 0 n − 1 { C n − 1 i ∗ i } =n*2^{n-1}+n*\sum_{i=1}^n\{C_{n-1}^{i-1}*(i-1)\}=n*2^{n-1}+n*\sum_{i=0}^{n-1}\{C_{n-1}^i*i\} =n∗2n−1+n∗i=1∑n{ Cn−1i−1∗(i−1)}=n∗2n−1+n∗i=0∑n−1{ Cn−1i∗i} = n ∗ 2 n − 1 + n ∗ ( n − 1 ) ∗ 2 n − 2 = ( n ∗ 2 + n ∗ ( n − 1 ) ) ∗ 2 n − 2 = n ∗ ( n + 1 ) ∗ 2 n − 2 =n*2^{n-1}+n*(n-1)*2^{n-2}=(n*2+n*(n-1))*2^{n-2}=n*(n+1)*2^{n-2} =n∗2n−1+n∗(n−1)∗2n−2=(n∗2+n∗(n−1))∗2n−2=n∗(n+1)∗2n−2

性质十一
∑ i = 0 n { ( C n i ) 2 } = C 2 ∗ n n \sum_{i=0}^n\{(C_n^i)^2\}=C_{2*n}^n i=0∑n{ (Cni)2}=C2∗nn
∑ i = 0 n { ( C n i ) 2 } = ∑ i = 0 n { C n i ∗ C n n − i } = C n + n n = C 2 ∗ n n \sum_{i=0}^n\{(C_n^i)^2\}=\sum_{i=0}^n\{C_n^i*C_n^{n-i}\}=C_{n+n}^n=C_{2*n}^n i=0∑n{ (Cni)2}=i=0∑n{ Cni∗Cnn−i}=Cn+nn=C2∗nn
错排数
把 n n n个分别写有 1 − n 1-n 1−n的球放进 n n n个固定的分别写有 1 − n 1-n 1−n的盒子里,每个盒子里正好有一个球且盒子上的数字与盒中球的数字都不相同的方案数,记作 D ( n ) D(n) D(n)
递推式:
D ( n ) = ( n − 1 ) ∗ ( D ( n − 1 ) + D ( n − 2 ) ) D ( 1 ) = 0 , D ( 2 ) = 1 D(n)=(n-1)*(D(n-1)+D(n-2))\ \ \ \ \ D(1)=0,D(2)=1 D(n)=(n−1)∗(D(n−1)+D(n−2)) D(1)=0,D(2)=1
证明:
第一个盒子有 n − 1 n-1 n−1种球可以放(除了一号球),假设第一个盒子放的 i i i号球,则有两种情况
①恰好第 i i i个盒子放的球就是一号球,则剩下的 n − 2 n-2 n−2个球继续错排,方案数为 D ( n − 2 ) D(n-2) D(n−2)
②第 i i i个盒子放的不是一号球,此时形成了一条新的限制:一号球不能放进 i i i号盒
除去第一个盒子和 i i i号球的剩下 n − 1 n-1 n−1个球和 n − 1 n-1 n−1个盒子,继续错排的方案数为 D ( n − 1 ) D(n-1) D(n−1)