利用矩阵求斐波那契数列

利用矩阵求斐波那契数列

flyfish 2015-8-27
矩阵（matrix）定义

一个m*n的矩阵是一个由m行n列元素排成的矩形阵列。矩阵里的元素可以是数字符号或者数学式.

形如

{acbd}

的数表称为 二阶矩阵，它由二行二列组成，其中a,b,c,d称为这个矩阵的元素。

形如

{x1x2}

的有序对称为 列向量Column vector

设

A={acbd}

X={x1x2}

则

Y={ax1+bx2cx1+dx2}

称为二阶矩阵A与平面向量X的乘积，记为AX=Y

斐波那契(Fibonacci)数列

从第三项开始，每一项都是前两项之和。
Fn = Fn − 1 + Fn − 2 , n⩾3

把斐波那契数列中 相邻的两项 Fn 和 Fn − 1 写成一个2 × 1的矩阵。
F0=0
F1=1

{FnFn−1}

={Fn−1+Fn−2Fn−1}

={1×Fn−1+1×Fn−21×Fn−1+0×Fn−2}

={1110}×{Fn−1Fn−2}

={1110}n−1×{F1F0}

={1110}n−1×{10}

求F(n)等于求二阶矩阵的n - 1次方，结果取矩阵第一行第一列的元素。

问题转换为二阶矩阵的n次幂

二阶矩阵的乘法
设

A={acbd},B={egfh},则AB={ae+bgce+dgaf+bhcf+dh}

矩阵A与矩阵B的积记做AB。

假设计算A的N次幂
方法1：
二阶矩阵的乘法满足结合律
设A,B,C都是任意的二阶矩阵
A(BC)=(AB)C

n=N/2 结果向下取整

AN=An∗An 当n为偶数
AN=An∗An∗A 当n为基数

相当于

A6=A3∗A3
A7=A3∗A3∗A
这样可以减少计算次数
因为
A6=A∗A∗A∗A∗A∗A 这里有5个乘
A6=（A∗A∗A）∗（A∗A∗A） 计算完A*A*A 得到结果 A3
再乘以 A3 这里用了3个乘

方法2
以计算 A6 为例
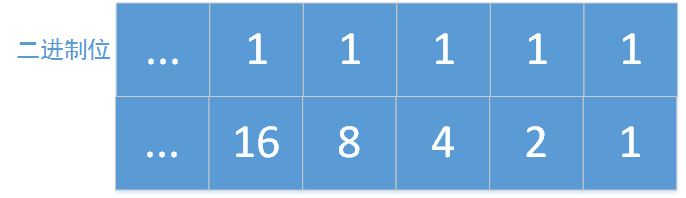
将6转化成二进制110
A6=A4∗A2

上图显示二进制与幂的指数关系
二进位为1需要乘，为0不需要乘

10进制7 = 二进制 111
例如 A7=A4∗A2∗A1
xie10进制31 = 二进制 11111
A31=A16∗A8∗A4∗A2∗A1

先写一个快速求幂的算法 该代码段是独立代码

#include 
//base 底数 ，exp 指数 
int qpow(int base,int exp)
{
if (0==exp ) return 1;

int ret=1;

while(exp)
{
    if(exp&1)//exp最右边一位 按位与&
    {
        ret=ret*base;
    }
    base=base*base;
    exp>>=1;//右移一位 
}
return ret;
} 

int main()
{
    printf("%d",qpow(3,5));
    return 0;
}

再写利用矩阵求斐波那契数列

#include
using namespace std;
class Matrix
{
public:
    void Init()  
    {         
        e_[0][0]=1;
        e_[0][1]=1;
        e_[1][0]=1;
        e_[1][1]=0; 
    }
    void Unit() //单位矩阵 
    {   
        e_[0][0]=1;
        e_[0][1]=0;
        e_[1][0]=0;
        e_[1][1]=1;        
    }
public:  
   int Get() const
   {
   return e_[0][1];
   }
    friend Matrix operator*(const Matrix& A,const Matrix& B)
    {
        Matrix AB;   
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        {   
            AB.e_[i][j]=0;
            for(int k=0;k<2;k++)
                AB.e_[i][j]+=A.e_[i][k]*B.e_[k][j];         
        }  
    return AB;
    }

private:
    __int64 e_[2][2];    

};

int qpow(Matrix& AB,int n) //矩阵快速幂 
{   
#define Bit(n) 1<
    Matrix t; 
    t.Init(); 
    for(int i=0;Bit(i)<=n;i++) 
    {   if(Bit(i)&n) AB=AB*t; 
        t=t*t;     
    }
    return AB.Get();    
}

调用方法

int n=10;
Matrix AB;
AB.Unit();
qpow(AB,n);//输出是55

代码中单位矩阵的解释
二阶方阵

{1001}

称为单位矩阵，通常记做E
对于任意二阶方阵A,都有 AE=EA=A
单位矩阵E在二阶方阵乘法的作用，相当于1在数的乘法中的作用。