【基础算法】(05)五大常用算法之一：分治算法

【基础算法】(05)五大常用算法之-分治算法

Auther: Thomas Shen
E-mail: [email protected]
Date: 2017/10/21
All Copyrights reserved !

---

1. 简述：

本系列介绍了五大常用算法，其中本文是第一篇，介绍了 ‘分治算法’ 的细节内容。

在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。

2. 算法原理：

2.1 基本思想：

分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

如果原问题可分割成k个子问题，1

2.2 分治法适用的情况：

分治法所能解决的问题一般具有以下几个特征：

1. 该问题的规模缩小到一定的程度就可以容易地解决;
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；

第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；

第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。

第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

2.3 分治法的基本步骤：

分治法在每一层递归上都有三个步骤：

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
2. 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题;
3. 合并：将各个子问题的解合并为原问题的解。

它的一般的算法设计模式如下：

    Divide-and-Conquer(P)
    1. if |P|≤n0
    2. then return(ADHOC(P))
    3. 将P分解为较小的子问题 P1 ,P2 ,...,Pk
    4. for i←1 to k
    5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
    6. T ← MERGE(y1,y2,...,yk) △ 合并子问题
    7. return(T)

其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。

ADHOC(P)是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。

算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。

2.4 复杂性分析：

一个分治法将规模为n的问题分成k个规模为 n／m 的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：T（n）= k T(n/m)+f(n)

通过迭代法求得方程的解：

递归方程及其解只给出n等于m的方幂时T(n)的值，但是如果认为T(n)足够平滑，那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。

通常假定T(n)是单调上升的，从而当 mi≤n 时，T(mi)≤T(n)。

---

3. 例题及实现：

可使用分治法求解的一些经典问题

1. 二分搜索;
2. 大整数乘法;
3. Strassen矩阵乘法;
4. 棋盘覆盖;
5. 归并排序;
6. 快速排序;
7. 线性时间选择;
8. 最接近点对问题;
9. 循环赛日程表;
10. 汉诺塔。

3.1 求x的n次幂：

复杂度为 O(lgn) 的分治算法:

#include "stdio.h"
#include "stdlib.h"

int power(int x, int n)
{
    int result;
    if(n == 1)
        return x;
    if( n % 2 == 0)
        result = power(x, n/2) * power(x, n / 2);
    else
        result = power(x, (n+1) / 2) * power(x, (n-1) / 2);
    return result;
}

int main()
{
    int x = 5;
    int n = 3;
    printf("power(%d,%d) = %d \n",x, n, power(x, n));
}

3.2 二分查找（分治算法）：

参考：http://blog.csdn.net/a19881029/article/details/23272127

1. 循环二分查找：

public class BinarySearch {  
    private int[] data;  

    public BinarySearch(int[] data){  
        this.data = data;  
    }  

    public int search(int target){  
        int min = 0;  
        int max = data.length - 1;  
        int n = 0;  
        while(true){  
            n = (min + max)/2;  
            if(target > data[n])  
                min = n + 1;  
            if(target < data[n])  
                max = n - 1;  
            if(target == data[n])  
                return n;  
            if(max < min)  
                return -1;  
        }  
    }  

    public static void main(String[] args) {  
        int[] ints = {1,2,7,9,25,44,66,99};  
        BinarySearch bs = new BinarySearch(ints);  
        System.out.println(bs.search(50));  
        System.out.println(bs.search(44));  
    }  
}  

2. 递归二分查找：

public class BinarySearch {  
    private int[] data;  

    public BinarySearch(int[] data){  
        this.data = data;  
    }  

    public int search(int target,int min,int max){  
        if(min > max)  
            return -1;  
        int n = (min + max)/2;  
        if(target > data[n])  
            min = n + 1;  
        if(target < data[n])  
            max = n -1;  
        if(target == data[n])  
            return n;  
        else  
            return search(target,min,max);  
    }  

    public static void main(String[] args) {  
        int[] ints = {1,2,7,9,25,44,66,99};  
        BinarySearch bs = new BinarySearch(ints);  
        System.out.println(bs.search(50,0,ints.length-1));  
        System.out.println(bs.search(44,0,ints.length-1));  
    }  
}  

3.3 最大子序列问题：

输入一组整数，求出这组数字子序列和中最大值。也就是只要求出最大子序列的和，不必求出最大的那个序列。例如：

序列：-2 11 -4 13 -5 -2，则最大子序列和为20。

1. 复杂度为O(N^2）的算法: 两层循环

#include   
#include   

int MaxSubSeqSum(const int *A, int N, int *start, int *end)  
{  
    int i = 0;  
    int j = 0;  
    int cur_sum = 0;  
    int Max_sum = 0;  

    for(i = 0; i < N; i ++)  
    {  
        cur_sum = 0;  
        for(j = i; j < N; j ++)  
        {  
            cur_sum += A[j];  
            if(cur_sum > Max_sum)  
            {  
                Max_sum = cur_sum;  
                *start = i;  
                *end   = j;  
            }  
        }  
    }  
    return Max_sum;  
}  

int main()  
{  
    int A[] = {-2,11,-4,13,-5,-2};  
    int start_index, end_index;  
    int max = MaxSubSeqSum(A,sizeof(A)/sizeof(A[0]),&start_index,&end_index);  
    printf("MaxSubSeqSum is %d -- %d \n",A[start_index],A[end_index]);  
    printf("max:%d \n",max);  
}  

2. 算法度为O(NlogN)的算法: 分治

采用的是“分治“(divide-and-conquer)策略。思想是把问题分成两个大致相当的子问题，然后递归地对他们求解，这是”分“。”治“阶段将两个子问题的解合并到一起，可能再做一些附加的工作，最终得到整个问题的解。

上述问题，把序列分为两部分，最大子序列可能出现在左半部分，或者右半部分，或者是两者之间。两者之间的情况下，先对左半部分求以最后一个数字为结尾的最大序列和。然后对右半部分以第一个数字开始算最大序列和，将两者加起来即是。

int Max_3(int a, int b, int c)  
{  
    if(a < b)  
        a = b;  
    if(a < c)  
        return c;  
    else  
        return a;  
}  
int MaxSubSeqSum2(const int *A, int left, int right)  
{  
    int MaxLeftSum, MaxRightSum, MaxSum;  
    int MaxLeftBorderSum, MaxRightBorderSum;  
    int LeftBorderSum, RightBorderSum;  
    int center;  
    int i;  
    if( left == right)  
    {  
        if(A[left] > 0)  
            return A[left];  
        else  
            return 0;  
    }  
    center = (left + right) / 2;  
    MaxLeftSum = MaxSubSeqSum2(A,left,center);  
    MaxRightSum = MaxSubSeqSum2(A,center + 1,right);  
    MaxLeftBorderSum = 0;  
    LeftBorderSum = 0;  

    for(i = center; i >= left; i--)  
    {  
        LeftBorderSum += A[i];  
        if(LeftBorderSum > MaxLeftBorderSum)  
            MaxLeftBorderSum = LeftBorderSum;  
    }  

    MaxRightBorderSum = 0;  
    RightBorderSum    = 0;  
    for(i = center + 1; i <= right; i++)  
    {  
        RightBorderSum += A[i];  
        if(RightBorderSum > MaxRightBorderSum)  
            MaxRightBorderSum = RightBorderSum;  
    }  
    MaxSum = Max_3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);  
    return MaxSum;  
}  

3. 算法复杂度为O(N)的算法:

/* 如果a[i]为负数，那么它不可能代表最优序列的起点，因为任何包含a[i]的  
 * 作为起点的子序列都可以通过用a[i+1]作为起点而得到改进。同理，任何小  
 * 于零的子序列不可能是最优子序列的前缀。
 */  
int MaxSubSeqSum3(const int *A, int N, int *start, int *end)  
{  
    int i = 0;  
    int j = 0;  
    int cur_sum = 0;  
    int Max_sum = 0;  

    for(i = 0; i < N; i ++)  
    {  
        cur_sum += A[i];  
        if(cur_sum > Max_sum)  
        {  
            Max_sum = cur_sum;  
                *end   = i;  
        }  

        else if(cur_sum < 0)  
        {  
            cur_sum = 0;  
            j = i + 1;  
        }  

        if(j <= *end)  
            *start = j;  

    }  

    return Max_sum;  
}  

int main()  
{  
    int A[] = {-2,11,-4,13,-5,-2};  
    int start_index, end_index;  
    int max = MaxSubSeqSum3(A,sizeof(A)/sizeof(A[0]),&start_index,&end_index);  
    printf("MaxSubSeqSum is %d -- %d \n",A[start_index],A[end_index]);  
    printf("max:%d \n",max);  
}  

3.4 棋盘覆盖：

转载自：http://www.cnblogs.com/Jason-Damon/archive/2013/
06/14/3136893.html

问题描述：
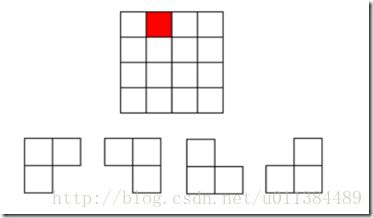
在一个2^k×2^k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

解题思路:
分析：当k>0时，将2k×2k棋盘分割为4个2^k-1×2^k-1 子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，如 (b)所示，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为棋盘1×1。（出自算法设计与分析-王晓东）

实现：每次都对分割后的四个小方块进行判断，判断特殊方格是否在里面。这里的判断的方法是每次先记录下整个大方块的左上角（top left coner）方格的行列坐标，然后再与特殊方格坐标进行比较，就可以知道特殊方格是否在该块中。如果特殊方块在里面，这直接递归下去求即可，如果不在，这根据分割的四个方块的不同位置，把右下角、左下角、右上角或者左上角的方格标记为特殊方块，然后继续递归。在递归函数里，还要有一个变量s来记录边的方格数，每次对方块进行划分时，边的方格数都会减半，这个变量是为了方便判断特殊方格的位置。其次还要有一个变nCount来记录L型骨牌的数量。

代码实现：

#include 
#include 

int nCount = 0;
int Matrix[100][100];

void chessBoard(int tr, int tc, int dr, int dc, int size);

int main()
{
    int size,r,c,row,col;
    memset(Matrix,0,sizeof(Matrix));
    scanf("%d",&size);
    scanf("%d%d",&row,&col);
    chessBoard(0,0,row,col,size);

    for (r = 0; r < size; r++)
    {
        for (c = 0; c < size; c++)
        {
            printf("%2d ",Matrix[r][c]);
        }
        printf("\n");
    }
    return 0;
}

void chessBoard(int tr, int tc, int dr, int dc, int size)
{
    //tr and tc represent the top left corner's coordinate of the matrix
    int s,t;
    if (1 == size) return;

    s = size/2; //The number of grid the matrix's edge
    t = ++ nCount;

    //locate the special  grid on bottom right corner
    if (dr < tr + s && dc < tc +s)
    {
        chessBoard(tr,tc,dr,dc,s);
    }
    else
    {
        Matrix[tr+s-1][tc+s-1] = t;
        chessBoard(tr,tc,tr+s-1,tc+s-1,s);
    }

    //locate the special  grid on bottom left corner
    if (dr < tr + s && dc >= tc + s )
    {
        chessBoard(tr,tc+s,dr,dc,s);
    }
    else
    {
        Matrix[tr+s-1][tc+s] = t;
        chessBoard(tr,tc+s,tr+s-1,tc+s,s);
    }

    //locate the special  grid on top right corner
    if (dr >= tr + s && dc < tc + s)
    {
        chessBoard(tr+s,tc,dr,dc,s);
    } 
    else
    {
        Matrix[tr+s][tc+s-1] = t;
        chessBoard(tr+s,tc,tr+s,tc+s-1,s);
    }

    //locate the special  grid on top left corner
    if (dr >= tr + s && dc >= tc + s)
    {
        chessBoard(tr+s,tc+s,dr,dc,s);
    } 
    else
    {
        Matrix[tr+s][tc+s] = t;
        chessBoard(tr+s,tc+s,tr+s,tc+s,s);
    }
}

程序结果：

---

References. ：

• [ 1 ]. Coursera | Java程序设计 | PKU
• [ 2 ]. 部分转载自： http://www.cnblogs.com/steven_oyj/archive/2010/
  05/22/1741370.html
• [ 3 ]. http://blog.csdn.net/zwhlxl/article/details/44086105
• [ 4 ]. http://www.cnblogs.com/butter-fly/archive/2016/07/03/5636514.html
• [ 5 ]. http://blog.csdn.net/a19881029/article/details/23272127
• [ 6 ]. http://www.cnblogs.com/Jason-Damon/archive/2013/06/14/
  3136893.html
• [ 7 ].
• [ 8 ].
• [ 9 ].
• [ 10 ].