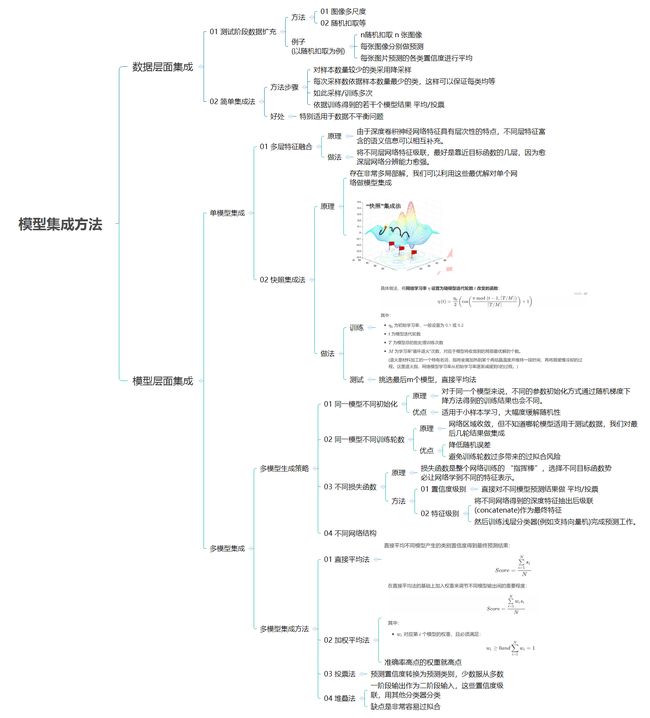
01 集成学习总结
文章目录
- 1 数据层面的集成
- 1.1 测试阶段数据扩充
- 1.2 “简单集成”法
- 2 模型层面的集成
- 2.1 单模型集成
- 2.1.1 多层特征融合
- 2.1.2 网络“快照”集成法
- 2.2 多模型集成
- 2.2.1 多模型生成策略
- 1) 同一模型不同初始化
- 2) 同一模型不同训练轮数
- 3) 不同损失函数
- 4) 不同网络结构
- 2.2.2 多模型集成方法
- 1) 直接平均法
- 2) 加权平均法
- 3) 投票法
- 4) 堆叠法(二次集成法)
历届kaggle竞赛冠军做法,或简单或复杂其最后一步必然是 集成学习,尽管模型已经很强大,但是集成学习往往能够起到锦上添花的作用。一般而言,深度学习的集成有两大层面:
- 数据层面
- 模型层面
1 数据层面的集成
1.1 测试阶段数据扩充
训练阶段有若干数据扩充策略,实际上在模型测试阶段也适用,例如:
- 图像多尺度(multi-scale)
- 随机扣取(random crop)
以随机扣取为例:
对测试图片可以得到 n n n张随机扣取图像,测试阶段只需要用训练好的深度网络模型对 n n n 张图分别做预测,之后将预测的各类置信度平均作为测试图像最终的测试结果即可。
1.2 “简单集成”法
“简单集成法”是Liu等人提出针对不平衡样本问题的一种简单集成学习解决方案,好处在于模型集成的同时还能缓解数据不平衡带来的问题,具体地说:
- 对于样本较多的类采取降采样(undersampling)
- 每次采样数依据样本数量最少的类别而定,这样每类取到的样本数可保持均等
采样结束后,针对每次采样得到的子数据集训练模型,如此采样、训练重复进行多次。最后对测试数据的预测则依据训练得到若干个模型的结果 取平均 / 投票 获得。
2 模型层面的集成
2.1 单模型集成
2.1.1 多层特征融合
由于深度卷积神经网络特征具有层次性的特点,不同层特征富含的语义信息可以相互补充。
在诸如下面这些领域常见 多层特征融合策略:
- 图像语义分割
- 细粒度图像检索
- 目标检测
一般地,多层特征融合操作可直接将不同层网络特征 级联(concatenate),而对于特征融合应选取哪些网络层,一个实际经验是:
最好使用靠近目标函数的几层卷积特征,因为愈深层特征包含的高层语义愈强,分辨能力也愈强。
相反,网络较浅层的特征较普适,用于特征融合反而起不到作用。
2.1.2 网络“快照”集成法
快照集成法 https://blog.csdn.net/qq_14845119/article/details/86509041
我们知道深度神经网络模型复杂的解空间中存在非常 多 的 局部最优解:
经典 Min-batch SGD
只能收敛到其中一个局部最优解。
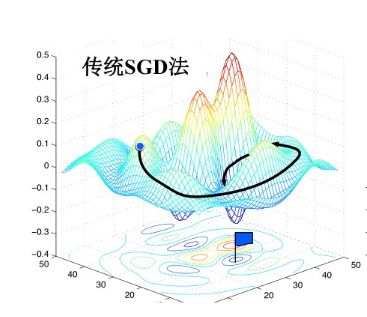
网络“快照”集成法
循环调整学习率依次收敛到不同的局部最优解处,利用这些最优解来对单个网络做模型集成。
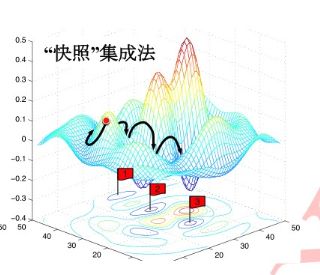
其差异如下:
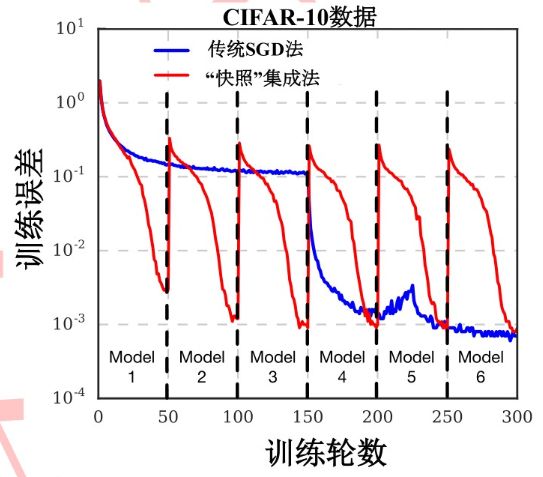
具体做法,将网络学习率 η \eta η 设置为随模型迭代轮数 t t t 改变的函数:
η ( t ) = η 0 2 ( cos ( π m o d ( t − 1 , ⌈ T / M ⌉ ) ⌈ T / M ⌉ ) + 1 ) \eta \left( t \right)=\frac{{{\eta }_{0}}}{2}\left( \cos \left( \frac{\pi \bmod \left( t-1,\left\lceil T/M \right\rceil \right)}{\left\lceil T/M \right\rceil } \right)+1 \right) η(t)=2η0(cos(⌈T/M⌉πmod(t−1,⌈T/M⌉))+1)
其中:
-
η 0 {{\eta }_{0}} η0 为初始学习率,一般设置为 0.1 或 0.2
-
t t t 为模型迭代轮数
-
T T T 为模型总的批处理训练次数
-
M M M 为学习率“循环退火”次数,对应于模型将收敛到的局部最优解的个数。
(退火是材料加工的一个特有名词,指将金属加热到某个再结晶温度并维持一段时间,再将其缓慢冷却的过程。这里退火指,网络模型学习率从初始学习率逐渐减缓到0的过程。)
学习率从 0.1 × 1 0.1 \times 1 0.1×1 随着 t t t 增长逐渐减缓到 0,之后将学习率重新放大从而跳出该局部最优解,如此往复。测试阶段,一般我们挑选最后 m m m个模型“快照”用于集成,这些模型“快照”可以采用“直接平均法”。
2.2 多模型集成
2.2.1 多模型生成策略
1) 同一模型不同初始化
对于同一个模型来说,不同的参数初始化方式通过随机梯度下降方法得到的训练结果也会不同。其非常适用于 小样本学习 场景:
- 首先对同一模型进行不同初始化
- 之后将得到的网络模型结果集成
其会大幅度缓解其随机性,提升最终任务的预测结果。
2) 同一模型不同训练轮数
若网络超参数设置得当,深度模型随着网络训练的进行会逐步趋于收敛,但不同训练轮数的结果仍有不同,无法确定到底哪一轮得到的模型最适用于测试数据,我们将最后几轮训练结果做集成。
- 可降低 随机误差,
- 另一方面避免了 训练 轮数过多 带来的 过拟合 风险。
3) 不同损失函数
损失函数是整个网络训练的 “指挥棒”,选择不同目标函数势必让网络学到不同的特征表示。以分类任务为例,可将例如:
- 交叉熵损失
- 合页损失
- 大间隔交叉熵损失
- 中心损失
作为损失函数分别训练模型。在预测阶段有两种做法:
- 置信度级别:直接对不同模型预测结果做 平均/投票。
- 特征级别:将不同网络得到的深度特征抽出后级联(concatenate)作为最终特征,然后训练浅层分类器(例如支持向量机)完成预测工作。
4) 不同网络结构
我们可以使用不同架构的网络训练模型,根据这些模型结果做集成。
2.2.2 多模型集成方法
假设共有 N N N 个模型待集成,对于某测试样本 x x x,其预测结果为 N N N 个 C C C 维向量( C C C 为数据的标记空间大小), s 1 , s 2 , . . . , s N s_1,s_2,...,s_N s1,s2,...,sN,我们介绍4种常用的多模型集成方法:
1) 直接平均法
直接平均不同模型产生的类别置信度得到最终预测结果:
S c o r e = ∑ i = 1 N s i N Score=\frac{\sum\limits_{i=1}^{N}{{{s}_{i}}}}{N} Score=Ni=1∑Nsi
2) 加权平均法
在直接平均法的基础上加入权重来调节不同模型输出间的重要程度:
S c o r e = ∑ i = 1 N w i s i N Score=\frac{\sum\limits_{i=1}^{N}{{{w}_{i}}{{s}_{i}}}}{N} Score=Ni=1∑Nwisi
其中:
- w i w_i wi 对应第 i i i 个模型的权重,且必须满足:
w i ≥ 0 a n d ∑ i = 1 N w i = 1 {{w}_{i}}\ge 0 and \sum\limits_{i=1}^{N}{{{w}_{i}}=1} wi≥0andi=1∑Nwi=1
实际使用中,权重 w i w_i wi 的取值可以根据不同模型在验证集上各自单独的准确率而定,简单说,准确率高点的权重高点,准确率低点权重就小点。
3) 投票法
最常用的就是多数表决法:需要先将各自模型返回的 预测置信度 s i s_i si 转化为 预测类别,即最高置信度对应的类别标记 c i ∈ { 1 , 2 , . . . , C } {{c}_{i}}\in \left\{ 1,2,...,C \right\} ci∈{1,2,...,C}作为该模型的预测结果。针对某个样本 x x x,下面将会分为两种情况 :
- 某个类别获得一半以上模型投票,则将样本标记为该类别
- 没有任何类别获得一半以上投票,则拒绝预测
但是这样有个问题,就是模型拒绝预测时候怎么办?一般我们采用相对多数投票法,很简单,少数服从多数,即投票数最多的类别作为最终预测结果。
4) 堆叠法(二次集成法)
一阶学习过程
样本 x x x 作为学习算法或网络模型的输入, s i s_i si作为第 i i i 个模型的类别置信度输出,该过程称为一阶学习过程。
二次集成法
堆叠法以 一阶学习过程的输出 作为 二阶学习过程输入,有时候也叫做元学习。拿刚才例子来说:
- 对于样本 x x x,输入是 N N N 个模型的预测置信度 s 1 , s 2 , . . . , s N s_1,s_2,...,s_N s1,s2,...,sN
- 这些置信度可以级联(concatenate)作为新的特征表示
- 基于这些 特征表示 训练学习期将其映射到样本原本的标记空间
注意此时的学习器可以为任何学习算法模型,如支持向量机、随机森林等,不过在此需要指出的是,堆叠法真的非常非常容易过拟合!