c#-二叉树数据结构及算法
Trees are a very common data structure in computer science. A tree is a
nonlinear data structure that is used to store data in a hierarchical manner.
We examine one primary tree structure in this chapter, the binary tree, along
with one implementation of the binary tree, the binary search tree. Binary
trees are often chosen over more fundamental structures, such as arrays and
linked lists, because you can search a binary tree quickly (as opposed to a
linked list) and you can quickly insert data and delete data from a binary tree
(as opposed to an array).
树是一种很常见的数据结构。树是一种按层次存储的非线性的数据结构。
本章我们讲一种主要的树结构--二叉树,以及二叉树的一种实现。
二叉树是一种基础的数据结构,如数组,链表,你可以快速地从二对树中查找数据(相比较链表)
而且你可以从二叉树中快递地插入和删除数据(相比较数组)。
THE DEFINITION OF A TREE
Before we examine the structure and behavior of the binary tree, we need to
define what we mean by a tree. A tree is a set of nodes connected by edges. An
example of a tree is a company’s organization chart (see Figure 12.1).
The purpose of an organization chart is to communicate to the viewer the
structure of the organization. In Figure 12.1, each box is a node and the
lines connecting the boxes are the edges. The nodes, obviously, represent
the entities (people) that make up an organization. The edges represent the
relationship between the entities. For example, the Chief Information Officer
(CIO), reports directly to the CEO, so there is an edge between these two
nodes. The IT manager reports to the CIO so there is an edge connecting
them. The Sales VP and the Development Manager in IT do not have a direct
edge connecting them, so there is not a direct relationship between these two
entities.
二叉树的定义
在讲解之前,我们先给出二叉树的定义。树是一组用边联结起的结点。有个公司行政图的例子
如下图:
此图的目的是给观众传达组织的体系。图中每一个方块是一个结点。联结这些方块的连接线是边。
很明显,这些结点代表组成公司的实体(人),这些边代表实体间的关系。比如,CIO直属CEO,
所以有一条连接CIO和CEO的线,之类的。![]()
Figure 12.2 displays another tree that defines a few terms we need when
discussing trees. The top node of a tree is called the root node. If a node is
connected to other nodes below it, the top node is called the parent, and
the nodes below it are called the parent’s children. A node can have zero,
one, or more nodes connected to it. Special types of trees, called binary trees,
restrict the number of children to no more than two. Binary trees have certain
computational properties that make them very efficient for many operations.
Binary trees are discussed extensively in the sections of this chapter. A node
without any child node is called a leaf.
Continuing to examine Figure 12.2, you can see that by following certain
edges, you can travel from one node to other nodes that are not
directly connected. The series of edges you follow to get from one node
to another is called a path (depicted in the figure with dashed lines). Visiting
all the nodes in a tree in some particular order is known as a tree
transversal.
下面的图显示了另一种树,顶部的结点叫做根结点。如果一个结点有被其他结点相连,上面的结点叫父结点,
下面的叫子结点。一个结点可以有0,1,或多个结点相连。有种特别的树,叫做二叉树,最多只能有两个子结点。
二叉树因为某种计算目的使得很多操作更有效。这一节大概说一下二叉树。没有子结点的结点叫叶子。
你可以从下图看到:沿着一些边,你可以从一个结点到另一个不直接相联的结点,这些边叫路径(图中的虚线)。
以一定的顺序查看所有的结点叫做遍历。
![]()
A tree can be broken down into levels. The root node is at Level 0, its
children at Level 1, those node’s children are at Level 2, and so on. A node at
any level is considered the root of a subtree, which consists of that root node’s
children, its children’s children, and so on. We can define the depth of a tree
as the number of layers in the tree.
Finally, each node in a tree has a value. This value is sometimes referred to
as the key value.
树 可以打断成很多层级。根结点是第0层,他的子结点是第1层。以此类推。
一个在任何层的结点都叫做根结点的子树。深度是指树的层数。
最后,每一个结点都有一个值,这个值有时被称为键值。
BINARY TREES
A binary tree is defined as a tree where each node can have no more than
two children. By limiting the number of children to 2, we can write efficient
programs for inserting data, deleting data, and searching for data in a binary
tree.
Before we discuss building a binary tree in C#, we need to add two
terms to our tree lexicon. The child nodes of a parent node are referred
to as the left node and the right node. For certain binary tree implementations,
certain data values can only be stored in left nodes and other data
values must be stored in right nodes. An example binary tree is shown in
Figure 12.3.
Identifying the child nodes is important when we consider a more specific
type of binary tree—the binary search tree. A binary search tree is a binary tree
where data with lesser values are stored in left nodes and values with greater
values are stored in right nodes. This property provides for very efficient
searches, as we shall soon see.
二叉树
树中的结点最多有两个子结点的树叫做二叉树。通过限制子结点,我们可以在二叉树中快速地插入,删除,查找数据。
之前我们讨论的C#中的二叉树,我们要增加两组词汇。父结点的子结点被称为左右结点,有二叉树的有些实现代码中,
左右结点存储的值是很讲究的,如下图的例子:
当我们考虑一种更具体的二叉树--二叉搜索树时,识别子结点是很重要的。二叉搜索树是一种小值在左,大值在右的二叉树。
这么做的目是让查找更快。
![]()
Building a Binary Search Tree
A binary search tree is made up of nodes, so we need a Node class that is
similar to the Node class we used in the linked list implementation. Let’s look
at the code for the Node class first:
建立一个二叉搜索树
二叉搜索树是由结点构成的,所以我们需要一个类似链表中的结点类。
We include Public data members for the data stored in the node and for
each child node. The displayNode method allows us to display the data stored
in a node. This particular Node class holds integers, but we could adopt the
class easily to hold any type of data, or even declare iData of Object type if we
need to.
Next we’re ready to build a BinarySearchTree (BST) class. The class consists
of just one data member—a Node object that represents the root node of the
BST. The default constructor method for the class sets the root node to null,
creating an empty node.
We next need an Insert method to add new nodes to our tree. This method
is somewhat complex and will require some explanation. The first step in
the method is to create a Node object and assign the data the Node holds
to the iData variable. This value is passed in as the only argument to the
method.
The second step to insertion is to see if our BST has a root node. If not,
then this is a new BST and the node we are inserting is the root node. If this
is the case, then the method is finished. Otherwise, the method moves on to
the next step.
If the node being added is not the root node, then we have to prepare to
traverse the BST in order to find the proper insertion point. This process is
similar to traversing a linked list. We need a Node object that we can assign
to the current node as we move from level to level. We also need to position
ourselves inside the BST at the root node.
Once we’re inside the BST, the next step is to determine where to put the
new node. This is performed inside a while loop that we break once we’ve
found the correct position for the new node. The algorithm for determining
the proper position for a node is as follows:
我们为每一个结点的数据存储加入public数据成员,displayNode函数允许我们查看结点中的数据。
这个结点类用整形存储数据,换成其他类型的也可以,只要你愿意。
接下来我们构建一个搜索二叉树的类(BST),这个类包括一个数据成员--一个代表根结点的结点对象。
默认构造函数把根结点置空,建立一个空的结点。
然后需要一个Insert函数用来添加新的结点。这个函数有时候会比较复杂,接下来会解释。
第一步:创建一个Node类的对象,将唯一的传入参数的值赋给data成员。
第二步:插入时先看BST是否有根结点。如果没有,则这个结点成为根结点。这种情况下函数返回,否则进入下一步。
第三步:如果插入的结点不是根结点,那么需要准备遍历这个BST来找到合适的插入点。这个过程就像遍历一个链表。
我们需要一个结点对象,这样我们就可以赋给当前的结点。我们也需要在BST内部自己定位。
一旦进入二叉树,接下来就决定往哪里放新结点,这一步j是在一个while循环内执行的,找到合适的位置后就break.
找合适位置的算法如下:
1. Set the parent node to be the current node, which is the root node.
2. If the data value in the new node is less than the data value in the current
node, set the current node to be the left child of the current node. If the
data value in the new node is greater than the data value in the current
node, skip to Step 4.
3. If the value of the left child of the current node is null, insert the new node
here and exit the loop. Otherwise, skip to the next iteration of the While
loop.
4. Set the current node to the right child node of the current node.
5. If the value of the right child of the current node is null, insert the new
node here and exit the loop. Otherwise, skip to the next iteration of the
While loop.
The code for the Insert method, along with the rest of the code for the BST
class (that has been discussed) and the Node class is as follows:
1,把父结点(也就是根结点)作为当前结点。
2,如果澵结点的值小于当前结点,把当前结点做为当前结点的左结点;如果新结点的值大于当前结点,去第4步
3,如果当前结点的左结点值为null,将新结点插入到这,然后退出循环。否则,进一入下轮循环。
4,设置当前结点到当前结点的右子结点。
5,如果当前结点的右结点为null,插入新结点到此,然后退出循环。否则,进一入下轮循环。
Insert函数的代码见下,紧接着BST类的其余代码:
Traversing a Binary Search Tree
We now have the basics to implement the BST class, but all we can do so far
is insert nodes into the BST.We need to be able to traverse the BST so that we
can visit the different nodes in several different orders.
There are three traversal methods used with BSTs: inorder, preorder, and
postorder. An inorder traversal visits all the nodes in a BST in ascending order
of the node key values. A preorder traversal visits the root node first, followed
by the nodes in the subtrees under the left child of the root, followed by the
nodes in the subtrees under the right child of the root. Although it’s easy
to understand why we would want to perform an inorder traversal, it is less
obvious why we need preorder and postorder traversals. We’ll show the code
for all three traversals now and explain their uses in a later section.
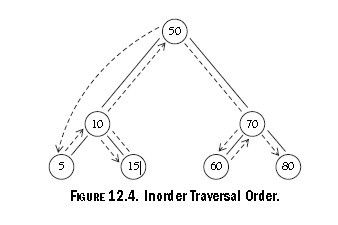
An inorder traversal can best be written as a recursive procedure. Since the
method visits each node in ascending order, the method must visit both the left
node and the right node of each subtree, following the subtrees under the left
child of the root before following the subtrees under the right side of the
root. Figure 12.4 diagrams the path of an inorder traversal.
Here’s the code for a inorder traversal method:
遍历二叉搜索树
我们有实现BST类的基础了,但是只能插入结点。我们需要用各种顺序遍历BST。
这里有三种方法:中序,前序,后序。
中序遍历的话先左,再中,再右。前序遍历先看根结点,然后是左,再右。
尽管很容易理解为什么我们想运行中序遍历,但是前序和后序的理由却不明显。后面会写出三种函数并且做出用法的解释。
中序遍历可以用递归完成。
To demonstrate how this method works, let’s examine a program that inserts
a series of numbers into a BST. Then we’ll call the inOrder method to display
the numbers we’ve placed in the BST. Here’s the code:
为了展示函数的原理,我们写一个程序,插入一串数据到BST中。然后中序遍历显示。
代码如下:
Here’s the output:
Inorder traversal:
结果如下:
3 16 22 23 37 45 99
This list represents the contents of the BST in ascending numerical order,
which is exactly what an inorder traversal is supposed to do.
Figure 12.5 illustrates the BST and the path the inorder traversal follows.
这串数字代表了BST的内容的升序。和中序遍历是一样的。
Now let’s examine the code for a preorder traversal:
前序遍历代码:
Notice that the only difference between the preOrder method and the inOrder
method is where the three lines of code are placed. The call to the displayNode
method was sandwiched between the two recursive calls in the inOrder
method and it is the first line of the preOrder method.
If we replace the call to inOrder with a call to preOrder in the previous
sample program, we get the following output:
Preorder traversal:
注意前序和中序的区别是三行代码的位置换了。前序遍历的结果如下:
23 16 3 22 45 37 99
Finally, we can write a method for performing postorder traversals:
最后是后序遍历代码:
Again, the difference between this method and the other two traversal
methods is where the recursive calls and the call to displayNode are placed.
In a postorder traversal, the method first recurses over the left subtrees and
then over the right subtrees. Here’s the output from the postOrder method:
Postorder traversal:
区别就是displayNode函数的位置换了。后序遍历先递归左子树和右子树。结果如下:
3 22 16 37 99 45 23
We’ll look at some practical programming examples using BSTs that use
these traversal methods later in this chapter.
接下来看一些使用了这些遍历函数的BST的例子
Finding a Node and Minimum/Maximum Values
in a Binary Search Tree
Three of the easiest things to do with BSTs are find a particular value, find the
minimum value, and find the maximum value. We examine these operations
in this section.
The code for finding the minimum and maximum values is almost trivial
in both cases, due to the properties of a BST. The smallest value in a BST will
always be found at the last left child node of a subtree beginning with the left
child of the root node. On the other hand, the largest value in a BST is found
at the last right child node of a subtree beginning with the right child of the
root node.
We provide the code for finding the minimum value first:
查找二叉搜索树中的最大最小值。在找一个具体值,最小值,最大值是BST中最容易的三件事。
找最大和最小值的代码都很琐碎。BST中的最小值一定在从根结点开始向左边找最后一个子树的左子结点。
最大值是从根结点开始向右边找最后一个子树的右子结点。找最小值的代码如下:
The method starts by creating a Node object and setting it to the root node
of the BST. The method then tests to see if the value in the left child is null. If
a non-Nothing node exists in the left child, the program sets the current node
to that node. This continues until a node is found whose left child is equal to
null. This means there is no smaller value below and the minimum value has
been found.
Now here’s the code for finding the maximum value in a BST:
函数从建立一个Node类的对象开始,然后把它设置成根结点,然后看左子结点的值是否为空。
如果一个左边不完全为空,那么把它设置成当前结点。一直这样继续直到找到结点的左边为空。
意思是没有更小的值了,最小值就在这。
下面是找最大值的代码:
This method looks almost identical to the FindMin() method, except the
method moves through the right children of the BST instead of the left
children.
这个函数和找最小值看上去像一样的,除了把Left换成Right.
The last method we’ll look at here is the Find method, which is used to
determine if a specified value is stored in the BST. The method first creates a
Node object and sets it to the root node of the BST. Next it tests to see if the
key (the data we’re searching for) is in that node. If it is, the method simply
returns the current node and exits. If the data isn’t found in the root node, the
data we’re searching for is compared to the data stored in the current node.
If the key is less than the current data value, the current node is set to the
left child. If the key is greater than the current data value, the current node is
set to the right child. The last segment of the method will return null as the
return value of the method if the current node is null (Nothing), indicating
the end of the BST has been reached without finding the key. When the While
loop ends, the value stored in current is the value being searched for.
Here’s the code for the Find method:
最后一个函数是查找函数,常用来看一个特特殊的值是否在树中。
函数首先建立一个结点并把根结点赋给它。然后看要找的值是不是在这个结点中。
如果在,那就直接返回这个结点。如果不在根结点中,就拿这个要找的值与当前结点中的值(key)做比较,
如果key比较要找的值小,把当前结点的左结点赋给当前结点。否则把当前结点的右结点赋给当前结点。
最后如果当前结点为null则函数返回null,说明BST没找到这个值,循环结束时,当前存储的值是所有找的值。
代码如下:
Removing a Leaf Node From a BST
The operations we’ve performed on a BST so far have not been that complicated,
at least in comparison with the operation we explore in this section—
removal. For some cases, removing a node from a BST is almost trivial; for
other cases, it is quite involved and demands that we pay special care to the
code we right, otherwise we run the risk of destroying the correct hierarchical
order of the BST.
Let’s start our examination of removing a node from a BST by discussing
the simplest case—removing a leaf. Removing a leaf is the simplest case since
there are no child nodes to take into consideration. All we have to do is set
each child node of the target node’s parent to null. Of course, the node will
still be there, but there will not be any references to the node.
The code fragment for deleting a leaf node is as follows (this code also
includes the beginning of the Delete method, which declares some data members
and moves to the node to be deleted):
将叶子结点移出BST
目前为止我们说的那些关于BST操作都不算复杂,至少比这一节的移除叶子来说是这样。
删除BST中的叶子结点很琐碎。要相当注意才能把代码写对。否则运行时可能有破坏BST的层次性的风险。
来讨论从BST中删除一个结点的简单情况--删除一个叶子结点。删除叶子是最简单的,因为不用考虑它的子结点。
我们需要做的就是把要删除的结点的父结点置为空。当然,结点还在这,只是没有它的任何引用了。
删除叶子结点的代码如下(同时包含了声明了一些数据成员的删除函数)
The while loop takes us to the node we’re deleting. The first test is to see if
the left child and the right child of that node are null. Then we test to see if
this node is the root node. If so, we set it to null, otherwise, we either set the
left node of the parent to null (if isLeftChild is true) or we set the right node
of the parent to null.
while循环将我们带到正在删除的结点,先if看左和右子结点是否为空。再看是不是根结点。
如果是,把它置为空,否则,将左子结点或右子结点的父结点置为空。
Deleting a Node With One Child
When the node to be deleted has one child, there are four conditions we have
to check for: 1. the node’s child can be a left child; 2. the node’s child can be
a right child; 3. the node to be deleted can be a left child; or 4. the node to be
deleted can be a right child.
Here’s the code fragment:
删除有一个子结点的结点
当要删除的结点有一个子结点时,有4种情况需要确认:
1,这个结点的子结点可以是左子结点
2,这个结点的子结点可以是右子结点
3,要被删除的结点可以是左结点
4,要被删除的结点可以是右结点
代码如下:
First, we test to see if the right node is null. If so, then we test to see if we’re
at the root. If we are, we move the left child to the root node. Otherwise, if the
node is a left child we set the new parent left node to the current left node,
or if we’re at a right child, we set the parent right node to the current right
node.
先看右结点是否为空,如果为空,则看我们是否在根结点,如果在,将左子结点移动到根结点。
否则的话,如果这个结点是一个我们将新父左结点设置给当前左结点的左结点,或者我们在右结点,
我们要将父右结点赋给当前结点。
Deleting a Node With Two Children
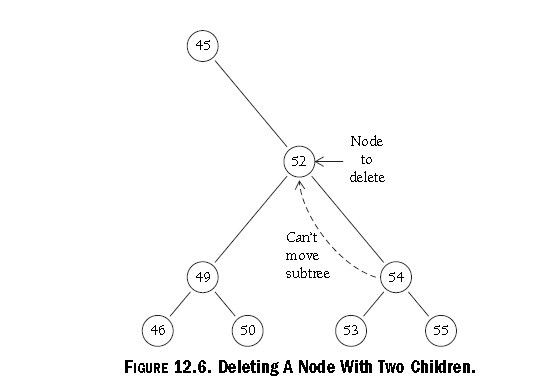
Deletion now gets tricky when we have to delete a node with two children.
Why? Look at Figure 12.6. If we need to delete the node marked 52, what do
we do to rebuild the tree. We can’t replace it with the subtree starting at the
node marked 54 because 54 already has a left child.
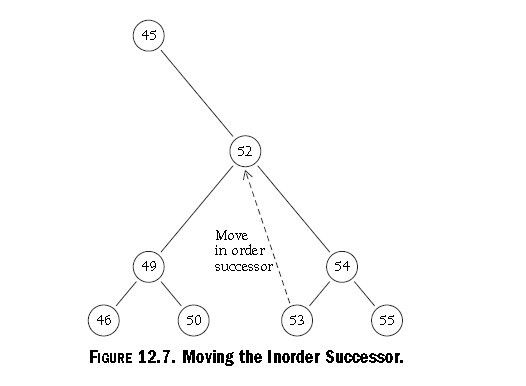
The answer to this problem is to move the inorder successor into the place
of the deleted node. This works fine unless the successor itself has children,
删除有两个子结点的结点
这种情况比较严峻。为啥?看下图,如果我们要删除52,我们该如何重建树。
我们不能用54替换子树,因为54有一个左子结点。
答案是这个问题需要将中序的后继移动到要删除的结点的位置。
除非后继有子结点,不然这样做还不错。
but there is a way around that scenario also. Figure 12.7 diagrams how using
the inorder successor works.
To find the successor, go to the original node’s right child. This node has
to be larger than the original node by definition. Then it begins following left
child paths until it runs out of nodes. Since the smallest value in a subtree
(like a tree) must be at the end of the path of left child nodes, following this
path to the end will leave us with the smallest node that is larger than the
original node
但是在这种情况倒也有一种方法,如下图。
要找到后继,去原始结点的右结点,这个结点比定义的原始结点要大。
然后它沿着左结点的路径直到跑出所有结点。因为子树的最小值一定在最后一个左结点。
沿着这个路径到底将会把我们与比原始结点大的最小的结点留在一起。
Here’s the code for finding the successor to a deleted node:
下面是找到要删除结点的后继结点的函数
Now we need to look at two special cases: the successor is the right child
of the node to be deleted and the successor is the left child of the node to be
deleted. Let’s start with the former.
First, the node to be deleted is marked as the current node. Remove this
node from the right child of its parent node and assign it to point to the
successor node. Then, remove the current node’s left child and assign to it
the left child node of the successor node. Here’s the code fragment for this
operation:
现在我们需要看一下这两种情况:要删除的结点的后继是右结点和后继是左结点的情况。
先看前一种:首先,要删除的结点被标记为当前结点,从它的父结点删除这个结点并且指向它的后继。
然后,删除当前结点的左子结点然后将它赋给后继的左子结点。代码片段如下:
Now let’s look at the situation when the successor is the left child of the
node to be deleted. The algorithm for performing this operation is as follows:
1. Assign the right child of the successor to the successor’s parent left child
node.
2. Assign the right child of the node to be deleted to the right child of the
successor node.
3. Remove the current node from the right child of its parent node and assign
it to point to the successor node.
4. Remove the current node’s left child from the current node and assign it to
the left child node of the successor node.
Part of this algorithm is carried out in the GetSuccessor method and part of it
is carried out in the Delete method. The code fragment from the GetSuccessor
method is:
现在来看当后继是要删除的结点的左子结点的情况。算法是这样实现的:
1,将后继的右子结点赋给后继的父结点的左子结点。
2,将要删除的结点的右子结点赋给后继的右子结点。
3,从它父结点的右子结点中移除当前结点并且赋给它指向后继。
4,从当前结点中移除其左子结点并且将它赋给后继的左子结点。
GetSuccessor函数的算法的部分代码如下
The code from the Delete method is:
Delete函数的代码如下
This completes the code for the Delete method. Because this code is somewhat
complicated, some binary search tree implementations simply mark
nodes for deletion and include code to check for the marks when performing
searches and traversals.
Here’s the complete code for Delete:
Delete函数的完整代码如下,因为代码比较复杂,一些二叉搜索树的实现简单地将“删除”标记在结点上,
当遍历时就检查是否有删除标记。
SUMMARY
Binary search trees are a special type of data structure called a tree. A tree is
a collection of nodes (objects that consist of fields for data and links to other
nodes) that are connected to other nodes. A binary tree is a specialized tree
structure where each node can have only two child nodes. A binary search
tree is a specialization of the binary tree that follows the condition that lesser
values are stored in left child nodes and greater values are stored in right
nodes.
Algorithms for finding the minimum and maximum values in a binary
search tree are very easy to write. We can also simply define algorithms for
traversing binary search trees in different orders (inorder, preorder, postorder).
These definitions make use of recursion, keeping the number of lines of code
to a minimum while making their analysis a bit harder.
Binary search trees are most useful when the data stored in the structure
are obtained in a random order. If the data in the tree are obtained in sorted or
close-to-sorted order, the tree will be unbalanced and the search algorithms
will not work as well.
小结:
二叉搜索树是一种特殊的树结构。树是互相连接的结点的集合。
二叉树是一种子结点最多只有两个结点的树。二叉搜索树是小在左,大在中的二叉树。
找最大和最小值的算法是很简单的。可以用前,中,后序遍历二叉树。
这些都可以用递归。保持代码行数最少。
二叉搜索树是当数据乱序时最有用的存储数据的结构。
如果树中的数据是排序好的,树就不平衡了,搜索算法就不起作用了。