DKRL: Representation Learning of Knowledge Graphs with Entity Descriptions 论文读书笔记
DKRL: Representation Learning of Knowledge Graphs with Entity Descriptions 论文读书笔记
1. Motivation
Knowledge graph embedding 将知识图中的实体和关系表示为低维的连续向量，从而使知识图谱可以适用于机器学习模型。 尽管Knowledge graph embedding已经有大量相关工作，但大多数方法仅仅集中在事实三元组（fact triples）上，而实体的补充文本描述（Textual descriptions）尚未得到充分利用。为此，本文提出了DKRL[1] 模型，此项工作为了融入实体描述的语义信息尝试了两个Encoder，包括连续词袋模型（CBOW）和一个基于卷积神经网络（CNN）的encoder，能够同时捕获图结构和语义信息。Entity descriptions 的示例如下图所示。
2. Methodology
1). Problem Formulation
此模型的每个实体有对应的两种表示，也即每个实体对应两个embedding：
- Structure-based Representations： 直接从图结构训练出的embedding，head和tail对应的embedding分别表示为 h s h_s hs 和 t s t_s ts.
- Description-based Representations： 由实体描述训练出来的embedding，head和tail对应的embedding分别表示为 h d h_d hd 和 t d t_d td.
2). Energy Function
E = E S + E D E = E_S + E_D E=ES+ED
其中 E S E_S ES 为structure-based representation的能量函数，和TransE[2]的定义一致。 E D E_D ED 为Description-based representation的能量函数，两个函数定义如下：
E S = ∣ ∣ h + r − t ∣ ∣ E_S = ||h + r -t|| ES=∣∣h+r−t∣∣
E D = E D D + E D S + E S D E_D = E_{DD} + E_{DS} + E_{SD} ED=EDD+EDS+ESD
上面的各部分定义如下：
E D D = ∣ ∣ h d + r − t d ∣ ∣ E_{DD} = ||h_d + r -t_d|| EDD=∣∣hd+r−td∣∣
E D S = ∣ ∣ h d + r − t s ∣ ∣ E_{DS} = ||h_d + r -t_s|| EDS=∣∣hd+r−ts∣∣
E S D = ∣ ∣ h s + r − t d ∣ ∣ E_{SD} = ||h_s + r -t_d|| ESD=∣∣hs+r−td∣∣
上述四个energy function将两类entity representation投射到同一个向量空间，两者互相促进逐步达到最优。
如下所示，对应的loss function与TransE的一致，不过与上述的四个energy function对应，对于每个head和tail为上述两种entity representation中的一种。
L = ∑ ( h , r , t ) ϵ T ∑ ( h , , r , , t , ) ϵ T , m a x ( γ + d ( h + r , t ) − d ( h , + r , , t , ) , 0 ) L = \sum_{(h,r,t)\epsilon T} \sum_{(h^,,r^,,t^,)\epsilon T^,} max(\gamma + d(h+r, t) -d(h^, + r^,, t^,),0) L=(h,r,t)ϵT∑(h,,r,,t,)ϵT,∑max(γ+d(h+r,t)−d(h,+r,,t,),0)
上面的d（）即为对应的energy function，上述的energy function定义为L1范式，作者在原文中提到在实验中对比了L1范式和L2范式，L1范式的性能更优
3). Encoder
a) CBOW Encoder
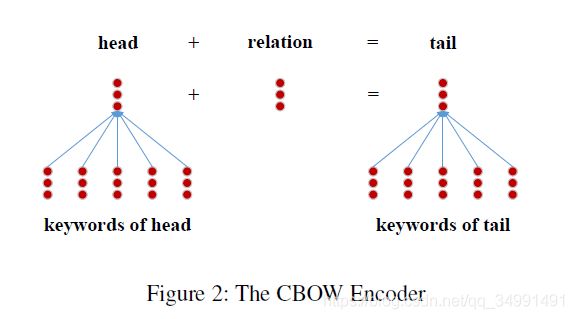
作者使用了类似TF-IDF的策略挑选出top k个entity description中的关键词，然后如下图所示，做简单的加和作为该实体的Description-based Representations。
b) CNN Encoder
首先每个词表示为一个 word embedding作为该CNN的第一层输入，作者在实验过程中初始值为word2vec预训练好的word embedding，在训练过程中不仅更新各个卷积核的参数，还会更新word embedding。如下图所示，该Encoder包括两层卷积层和两层Pooling层。对于每个卷积层，都会有一个size为k、步长为1的sliding window来对前一层的输入做卷积，示意图中的size k取值为3. 卷积操作的方式与标准的CNN一样。这里两层pooling， 第一层为max pooling，第二层为mean pooling。
3. Experiments
1). Dataset
FB15K and FB20K
2). Task
Knowledge Graph Completion
-
评测方案： 通过计算候选三元组的score值S(h，r， t) = ||h + r - t||，得到一个ranking列表。通过计算原三元组的mean rank 和HITS@10（rank值不大于10的比例）来进行评测. 作者使用两种entity representation的加权求和作为head和tail的embedding。同时作者还比较了只用Description-based Representations的对应的两类Encoder的结果。
-
评测结果
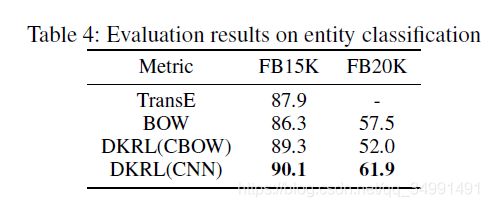
Entity Classification
- 评测方案： 使用两种entity representation的加权求和作为分类的输入特征。
- 评测结果：
Code: https://github.com/thunlp/DKRL
Reference
[1] Xie, Ruobing, et al. “Representation learning of knowledge graphs with entity descriptions.” Thirtieth AAAI Conference on Artificial Intelligence. 2016.