力扣高频|算法面试题汇总(八):排序与检索
力扣高频|算法面试题汇总(一):开始之前
力扣高频|算法面试题汇总(二):字符串
力扣高频|算法面试题汇总(三):数组
力扣高频|算法面试题汇总(四):堆、栈与队列
力扣高频|算法面试题汇总(五):链表
力扣高频|算法面试题汇总(六):哈希与映射
力扣高频|算法面试题汇总(七):树
力扣高频|算法面试题汇总(八):排序与检索
力扣高频|算法面试题汇总(九):动态规划
力扣高频|算法面试题汇总(十):图论
力扣高频|算法面试题汇总(十一):数学&位运算
力扣高频|算法面试题汇总(八):排序与检索
力扣链接
目录:
- 1.最大数
- 2.摆动排序 II
- 3.寻找峰值
- 4.寻找重复数
- 5.计算右侧小于当前元素的个数
1.最大数
给定一组非负整数,重新排列它们的顺序使之组成一个最大的整数。
示例 1:
输入: [10,2]
输出: 210
示例 2:
输入: [3,30,34,5,9]
输出: 9534330
说明: 输出结果可能非常大,所以你需要返回一个字符串而不是整数。
思路:
刚开始直接想的就是用字典排序,然后进行字符串拼接,但是遇到输入[3,30,34,5,9],会得到输出9534303,但真正的最大值应该是9534330,所有需要自定义排序,比较 30 + 3 > 3 + 30 ? 30+3 > 3+30? 30+3>3+30?。
C++
class Solution {
public:
static bool cmp(string& num1, string& num2) {
string n1 = num1 + num2;
string n2 = num2 + num1;
return n1 > n2;
}
string largestNumber(vector<int>& nums) {
vector<string> strNum;
for(int i = 0; i < nums.size(); ++i){
strNum.push_back(to_string(nums[i]));
}
sort(strNum.begin(), strNum.end(), cmp);
string num;
if (strNum[0] == "0")//考虑全零的情况
return "0";
for(int i = 0; i < strNum.size(); ++i)
num += strNum[i];
return num;
}
};
Python
import functools
class Solution:
def largestNumber(self, nums):
# 自定义排序
nums = sorted(nums, key=functools.cmp_to_key(self.cmp))
if nums[0] == 0:
return "0"
num = ""
for n in nums:
num += str(n)
return num
def cmp(self, num1, num2):
if str(num1) + str(num2) > str(num2) + str(num1):
return -1
else:
return 1
2.摆动排序 II
给定一个无序的数组 nums,将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。
示例 1:
输入: nums = [1, 5, 1, 1, 6, 4]
输出: 一个可能的答案是 [1, 4, 1, 5, 1, 6]
示例 2:
输入: nums = [1, 3, 2, 2, 3, 1]
输出: 一个可能的答案是 [2, 3, 1, 3, 1, 2]
说明:
你可以假设所有输入都会得到有效的结果。
进阶:
你能用 O(n) 时间复杂度和 / 或原地 O(1) 额外空间来实现吗?
思路:
参考大佬的思路:
1.先把数组排序,如把[1, 3, 2, 2, 3, 1],排序成[1,1,2,2,3,3]
2.拆分成两个数组:奇数组[1,1,2]和偶数组[2,3,3],如果无法等分,保证奇数组长度大于偶数组长度即可,因为是把偶数组穿插到技术组中,且数组是升序。
3.把奇数组和偶数组分别逆序,如[2,1,1]和[3,3,2]。
4.偶数组穿插到奇数中:[2,3,1,3,1,2]
5.算法的实现复杂度 O ( n l o g n ) O(nlogn) O(nlogn),空间复杂度 O ( n ) O(n) O(n)
C++
class Solution {
public:
void wiggleSort(vector<int>& nums) {
// 先排序
sort(nums.begin(), nums.end());
// 辅助数组
vector<int> tempOdd;
vector<int> tempEven;
tempOdd.assign(nums.begin(), nums.begin() + (nums.size() +1)/ 2 );// 加1保证奇数数组比偶数数组大
tempEven.assign(nums.begin() + (nums.size()+1) / 2, nums.end());// 这是因为偶数数组来穿插到奇数数组中
// 逆序穿插
int k = tempOdd.size() - 1;
for (int i = 0; i < nums.size(); i += 2) {
cout << "k:" << k << endl;
nums[i] = tempOdd[k--];
}
k = tempEven.size() - 1;
for (int i = 1; i < nums.size(); i += 2) {
cout << "k:" << k << endl;
nums[i] = tempEven[k--];
}
}
};
Python:
class Solution:
def wiggleSort(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
getNum = sorted(nums)
tempOdd = getNum[: (len(nums)+1)//2]
tempEven = getNum[(len(nums)+1)//2:]
k = len(tempOdd) - 1
for i in range(0, len(nums), 2):
nums[i] = tempOdd[k]
k -= 1
k = len(tempEven) - 1
for i in range(1, len(nums), 2):
nums[i] = tempEven[k]
k -= 1
思路2:
实现复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)的算法,还是参考刚刚的参考大佬的思路:
1.使用快速选择找到数组的中位数,实现时间复杂度 O ( n ) O(n) O(n)。因为不关心奇偶数组的内部排序,只关心奇数组的最大值小于等于偶数组的最小值(临界点),这个邻接点就是中位数。
2.使用虚地址进行映射,实现空间复杂度 O ( 1 ) O(1) O(1),(这个nb),不够和上述思路不一样的是:上述思路是将奇数组(较小的数组)排前面,偶数组(较大的数组)排后面,现在将较大的数组排前面,较小的数组放后面,方便地址映射:#define A(i) nums[(1+2*(i)) % (n|1)]
C++
class Solution {
public:
void wiggleSort(vector<int>& nums) {
int n = nums.size();
// Find a median.
auto midptr = nums.begin() + n / 2;
nth_element(nums.begin(), midptr, nums.end());
int mid = *midptr;
// Index-rewiring.
#define A(i) nums[(1+2*(i)) % (n|1)]
// 3-way-partition-to-wiggly in O(n) time with O(1) space.
int i = 0, j = 0, k = n - 1;
while (j <= k) {
if (A(j) > mid)
swap(A(i++), A(j++));
else if (A(j) < mid)
swap(A(j), A(k--));
else
j++;
}
}
};
3.寻找峰值
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。
示例 1:
输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
说明:
你的解法应该是 O(logN) 时间复杂度的。
思路:
比较num[i]和num[i+1]的值即可。
峰值出现一般有三种情况:
- 1.数据呈现递增的趋势,那么峰值在末尾。
- 2.数据呈现递减的趋势,那么峰值在开头。
- 3.数据成波动的形式,那么峰值在第一个出现
nums[i] > nums[i+1]的地方。 - 4.算法时间复杂度: O ( n ) O(n) O(n)
C++
class Solution {
public:
int findPeakElement(vector<int>& nums) {
for(int i = 0; i <nums.size() - 1; ++i)
if(nums[i] > nums[i+1])
return i;
return nums.size() -1;
}
};
Python
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
for i in range(len(nums) -1):
if nums[i] > nums[i+1]:
return i
return len(nums)-1
思路2:
使用递归。 每次计算start和end的中间数mid。如果mid大于mid+1的数,则峰值在左边,否则在右边。边界条件为:end == start。
时间复杂度 : O ( l o g n ) O(logn) O(logn),空间复杂度 O ( l o g n ) O(logn) O(logn)。
class Solution {
public:
int findPeakElement(vector<int>& nums) {
// 输入 数组、 起始点、 截止点、 中间数
return findPeakElementCore(nums, 0, nums.size() - 1);
}
int findPeakElementCore(vector<int>& nums, int start, int end){
if(start == end)
return start;
int mid = (end + start)/ 2 ;
if(nums[mid] <= nums[mid + 1])
return findPeakElementCore(nums, mid + 1, end);// 峰值在右边
else
return findPeakElementCore(nums, start, mid);// 峰值在左边
}
};
Python
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
return self.findPeakElementCore(nums, 0 , len(nums) - 1)
def findPeakElementCore(self, nums, start, end):
if start == end:
return start
mid = (start + end)//2
if nums[mid] <= nums[mid + 1]:
return self.findPeakElementCore(nums, mid + 1, end)
else:
return self.findPeakElementCore(nums, start, mid)
思路3:
在思路2的基础上进一步优化,使用迭代递归,这样时间复杂度不变,但空间复杂度降为 O ( 1 ) O(1) O(1)
C++
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int start = 0;
int end = nums.size() - 1;
while(start < end){
int mid = (start + end)/2;
if(nums[mid] < nums[mid+ 1] )
start = mid + 1;
else
end = mid;
}
return start;
}
};
Python
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
start = 0
end = len(nums) - 1
while start < end:
mid = (start + end) // 2
if nums[mid] <= nums[mid + 1]:
start = mid + 1
else:
end = mid
return start
4.寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
不能更改原数组(假设数组是只读的)。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字,但它可能不止重复出现一次。
思路:
先进行排序,重复的数字必定相邻,时间复杂度 O ( n l g n + n ) O(nlgn + n) O(nlgn+n),空间复杂度 O ( 1 ) ( o r O ( n ) ) O(1)(orO(n)) O(1)(orO(n))。产生副本为O(n)。
C++
class Solution {
public:
int findDuplicate(vector<int>& nums) {
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size() - 1; ++i){
if(nums[i] == nums[i + 1])
return nums[i];
}
return 0;
}
};
Python
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
nums = sorted(nums)
for i in range(len(nums) - 1):
if nums[i] == nums[i+1]:
return nums[i]
return 0
思路2:
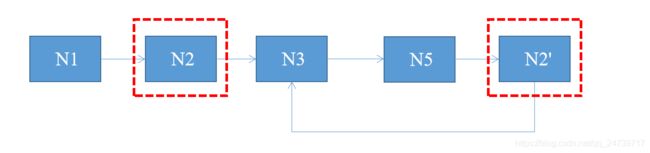
把数据想象成链表,使用快慢指针查找。
数组:num[val] = next,起索引模拟成链表的值,其索引对应的值模拟成下一个链表的地址(索引)。由于存在重复的数字,在存在相同的映射,使得这个链表成环。如val1 = val2,则num[val1] = num[val2];。
步骤如下:
- 1.先使用快慢指针找到第一个相遇的点。
- 2.把慢指针复位为0,快指针位置不变,但没错移动和慢指针一样,只移动一次。
- 3.快慢指针相遇的前一个点,则为重复的数字。
这个思路和环形链表找到入口节点基本一致。这个时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
C++
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int pFast = 0;
int pSlow = 0;
do{
pFast = nums[pFast];
pFast = nums[pFast];
pSlow = nums[pSlow];
}while(pFast != pSlow);
//cout<<"pFast:"<
pSlow = 0;
while(nums[pFast] != nums[pSlow]){
pSlow = nums[pSlow];
pFast = nums[pFast];
}
return nums[pFast];
}
};
Python:
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
pFast = 0
pSlow = 0
while True:
pFast = nums[pFast]
pFast = nums[pFast]
pSlow = nums[pSlow]
if pSlow == pFast:
break
pSlow = 0
while nums[pFast] != nums[pSlow]:
pFast = nums[pFast]
pSlow = nums[pSlow]
return nums[pSlow]
5.计算右侧小于当前元素的个数
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.
思路:
参考大佬巧妙的思路,总结一下:
1.从右往左遍历,因为需要记录比遍历数字小的元素,所以用一个排序数组(从小到大)存储每一次遍历的结果。
2.获取遍历的元素,计算这个元素插入需要插入到这个排序数组中的索引,由于数组是从小到大的,那么这个索引其实就是比当前数字小的个数。
3.把索引值放入结果中。
4.逆序输出结果。
算法的复杂度的上界为: O ( n l o g n ) O(nlogn) O(nlogn)
C++
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> sortNums;
vector<int> res;
for(auto itear = nums.rbegin(); itear < nums.rend(); ++itear){
// 寻找索引
// lower_bound()返回第一个大于等于x的数的地址
int index = lower_bound(sortNums.begin(), sortNums.end(), *itear) - sortNums.begin();
res.push_back(index);
// 插入排序数组
sortNums.insert(sortNums.begin() + index, *itear);
}
// 逆序
reverse(res.begin(),res.end());
return res;
}
};
Python:
class Solution:
def countSmaller(self, nums: List[int]) -> List[int]:
sortList = []
res = []
for num in reversed(nums):
# 判断数字的插入位置 索引对应即有多少个比当前小数字小的数字
index = bisect.bisect_left(sortList, num)
# 索引即结果,存储
res.append(index)
# 将数字插入排序列表
sortList.insert(index, num)
# 逆序输出
return res[::-1]