matlab代码---聚类分析
利用Matlab和SPSS软件实现聚类分析
- 用Matlab编程实现
1.1运用Matlab中的一些基本矩阵计算方法,通过自己编程实现聚类算法,在此只讨论根据最短距离规则聚类的方法。
调用函数:
min1.m——求矩阵最小值,返回最小值所在行和列以及值的大小
min2.m——比较两数大小,返回较小值
std1.m——用极差标准化法标准化矩阵
ds1.m——用绝对值距离法求距离矩阵
cluster.m——应用最短距离聚类法进行聚类分析
print1.m——调用各子函数,显示聚类结果
聚类分析算法
假设距离矩阵为vector, a阶,矩阵中最大值为max,令矩阵上三角元素等于max
聚类次数=a-1,以下步骤作a-1次循环:
求改变后矩阵的阶数,计作c
求矩阵最小值,返回最小值所在行e和列f以及值的大小g
for l=1:c,为vector(c+1,l)赋值,产生新类
令第c+1列元素,第e行和第f行所有元素为,第e列和第f列所有元素为max
源程序如下:
%std1.m,用极差标准化法标准化矩阵
function std=std1(vector)
max=max(vector); %对列求最大值
min=min(vector);
[a,b]=size(vector); %矩阵大小,a为行数,b为列数
for i=1:a
for j=1:b
std(i,j)= (vector(i,j)-min(j))/(max(j)-min(j));
end
end
%ds1.m,用绝对值法求距离
function d=ds1(vector);
[a,b]=size(vector);
d=zeros(a);
for i=1:a
for j=1:a
for k=1:b
d(i,j)=d(i,j)+abs(vector(i,k)-vector(j,k));
end
end
end
fprintf('绝对值距离矩阵如下:\n');
disp(d)
%min1.m,求矩阵中最小值,并返回行列数及其值
function [v1,v2,v3]=min1(vector);%v1为行数,v2为列数,v3为其值
[v,v2]=min(min(vector'));
[v,v1]=min(min(vector));
v3=min(min(vector));
%min2.m,比较两数大小,返回较小的值
function v1=min(v2,v3);
if v2>v3
v1=v3;
else
v1=v2;
end
%cluster.m,最短距离聚类法
function result=cluster(vector);
[a,b]=size(vector);
max=max(max(vector));
for i=1:a
for j=i:b
vector(i,j)=max;
end
end;
for k=1:(b-1)
[c,d]=size(vector);
fprintf('第%g次聚类:\n',k);
[e,f,g]=min1(vector);
fprintf('最小值=%g,将第%g区和第%g区并为一类,记作G%g\n\n',g,e,f,c+1);
for l=1:c
if l<=min2(e,f)
vector(c+1,l)=min2(vector(e,l),vector(f,l));
else
vector(c+1,l)=min2(vector(l,e),vector(l,f));
end
end;
vector(1:c+1,c+1)=max;
vector(1:c+1,e)=max;
vector(1:c+1,f)=max;
vector(e,1:c+1)=max;
vector(f,1:c+1)=max;
end
%print1,调用各子函数
function print=print1(filename,a,b); %a为地区个数,b为指标数
fid=fopen(filename,'r')
vector=fscanf(fid,'%g',[a b]);
fprintf('标准化结果如下:\n')
v1=std1(vector)
v2=ds1(v1);
cluster(v2);
%输出结果
print1('fname',9,7)
1.2 k-means聚类分析
function y=kMeansCluster(m,k,isRand)
%%%%%%%%%%%%%%%%
%
% kMeansCluster - Simple k means clustering algorithm
% Author: Kardi Teknomo, Ph.D.
%
% Purpose: classify the objects in data matrix based on the attributes
% Criteria: minimize Euclidean distance between centroids and object points
% For more explanation of the algorithm, see http://people.revoledu.com/kardi/tutorial/kMean/index.html
% Output: matrix data plus an additional column represent the group of each object
%
% Example: m = [ 1 1; 2 1; 4 3; 5 4] or in a nice form
% m = [ 1 1;
% 2 1;
% 4 3;
% 5 4]
% k = 2
% kMeansCluster(m,k) produces m = [ 1 1 1;
% 2 1 1;
% 4 3 2;
% 5 4 2]
% Input:
% m - required, matrix data: objects in rows and attributes in columns
% k - optional, number of groups (default = 1)
% isRand - optional, if using random initialization isRand=1, otherwise input any number (default)
% it will assign the first k data as initial centroids
%
% Local Variables
% f - row number of data that belong to group i
% c - centroid coordinate size (1:k, 1:maxCol)
% g - current iteration group matrix size (1:maxRow)
% i - scalar iterator
% maxCol - scalar number of rows in the data matrix m = number of attributes
% maxRow - scalar number of columns in the data matrix m = number of objects
% temp - previous iteration group matrix size (1:maxRow)
% z - minimum value (not needed)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if nargin<3, isRand=0; end
if nargin<2, k=1; end
[maxRow, maxCol]=size(m)
if maxRow<=k,
y=[m, 1:maxRow]
else
% initial value of centroid
if isRand,
p = randperm(size(m,1)); % random initialization
for i=1:k
c(i,:)=m(p(i),:)
end
else
for i=1:k
c(i,:)=m(i,:) % sequential initialization
end
end
temp=zeros(maxRow,1); % initialize as zero vector
while 1,
d=DistMatrix(m,c); % calculate objcets-centroid distances
[z,g]=min(d,[],2); % find group matrix g
if g==temp,
break; % stop the iteration
else
temp=g; % copy group matrix to temporary variable
end
for i=1:k
f=find(g==i);
if f % only compute centroid if f is not empty
c(i,:)=mean(m(find(g==i),:),1);
end
end
end
y=[m,g];
end
The Matlab function kMeansCluster above call function DistMatrix as shown in the code below. It works for multi-dimensional Euclidean distance. Learn about other type of distance here.
function d=DistMatrix(A,B)
%%%%%%%%%%%%%%%%%%%%%%%%%
% DISTMATRIX return distance matrix between points in A=[x1 y1 ... w1] and in B=[x2 y2 ... w2]
% Copyright (c) 2005 by Kardi Teknomo, http://people.revoledu.com/kardi/
%
% Numbers of rows (represent points) in A and B are not necessarily the same.
% It can be use for distance-in-a-slice (Spacing) or distance-between-slice (Headway),
%
% A and B must contain the same number of columns (represent variables of n dimensions),
% first column is the X coordinates, second column is the Y coordinates, and so on.
% The distance matrix is distance between points in A as rows
% and points in B as columns.
% example: Spacing= dist(A,A)
% Headway = dist(A,B), with hA ~= hB or hA=hB
% A=[1 2 3; 4 5 6; 2 4 6; 1 2 3]; B=[4 5 1; 6 2 0]
% dist(A,B)= [ 4.69 5.83;
% 5.00 7.00;
% 5.48 7.48;
% 4.69 5.83]
%
% dist(B,A)= [ 4.69 5.00 5.48 4.69;
% 5.83 7.00 7.48 5.83]
%%%%%%%%%%%%%%%%%%%%%%%%%%%
[hA,wA]=size(A);
[hB,wB]=size(B);
if wA ~= wB, error(' second dimension of A and B must be the same'); end
for k=1:wA
C{
k}= repmat(A(:,k),1,hB);
D{
k}= repmat(B(:,k),1,hA);
end
S=zeros(hA,hB);
for k=1:wA
S=S+(C{
k}-D{
k}').^2;
end
d=sqrt(S);
%这是一个简单的k均值聚类批处理函数
%待分类的样本x=mvnrnd(mu,siguma,20)
%idx3=kmeans(x,3,'distance','city');或者
%idx4=kmeans(x,4,'dist','city','display','iter');这个可以显示出每次迭代的距离和
%显示分类轮廓图[silh4,h]=silhouette(x,idx4,'city');xlable('silhouette
% value');ylable('cluster')
%mean(silh5) 结果越接近1越好
mu1=[1,1];
sigma1=[0.5 0;0 0.5];
x1=mvnrnd(mu1,sigma1,10);
mu2=[7,7];
sigma2=[0.5 0;0 0.5];
x2=mvnrnd(mu2,sigma2,10);
x=[x1;x2]
plot(x(:,1),x(:,2),'bo');
[idx2,c]=kmeans(x,2,'dist','city','display','iter');
figure(2);
[silh2,h]=silhouette(x,idx2,'city');
%xlable('silhouette value')
%ylable('cluster')
figure(3);
plot(x(idx2==1,1),x(idx2==1,2),'r+',x(idx2==2,1),x(idx2==2,2),'b.');
'分类水平:(1为最好):'
a=mean(silh2);
a
'图心矩阵为:'
c
1.3 模糊聚类分析
缺少main.m
mhjl_1.m
%模糊聚类程序
function f=mujl(x,lamda)
%输入原始数据以及lamda的值
if lamda>1
disp('error!') %错误处理
end
[n,m]=size(x);
xmax=max(x);xmin=min(x);
x=(x-xmin(ones(n,1),:))./(xmax(ones(n,1),:)-xmin(ones(n,1),:))
y=pdist(x);
disp('欧式距离矩阵:');
dist=squareform(y) %欧氏距离矩阵
dmax=dist(1,1);
for i=1:n
for j=1:n
if dist(i,j)>dmax
dmax=dist(i,j);
end
end
end
disp('处理后的欧氏距离矩阵,其特点为每项元素均不超过1:');
sdist=dist/dmax %使距离值不超过1
disp('模糊关系矩阵:');
r=ones(n,n)-sdist %计算对应的模糊关系矩阵
t=mhdj(r);
le=t-r;
while all(all(le==0)==0)==1 %如果t与r相等,则继续求r乘以r
r=t;
t=mhdj(r);
le=t-r;
end
disp('模糊等价矩阵为:')
t
for i=1:n
k=1;
for j=1:n
if t(i,j)>=lamda
group(i,k)=j;
k=k+1;
end
end
end
disp('聚类结果如下(数字0为自动填充数据,不是样本序号):')
group(1,:)
gru_val=1;
for i=2:n
k=0;
for j=1:i-1
if all(group(i,:)==group(j,:))==1 %两行值完全相等,不输出
k=1;break;
end
end
if k==0
disp('第i类样本序号:'),i
gru_val=gru_val+1;
disp(group(i,:)) %仅输出不重复的分类
end
end
gru_val
mhjl.m
%模糊聚类程序
function f=mujl(x,lamda)
%输入原始数据以及lamda的值
if lamda>1
disp('error!') %错误处理
end
[n,m]=size(x);
y=pdist(x);
disp('欧式距离矩阵:');
dist=squareform(y) %欧氏距离矩阵
dmax=dist(1,1);
for i=1:n
for j=1:n
if dist(i,j)>dmax
dmax=dist(i,j);
end
end
end
disp('处理后的欧氏距离矩阵,其特点为每项元素均不超过1:');
sdist=dist/dmax %使距离值不超过1
disp('模糊关系矩阵:');
r=ones(n,n)-sdist %计算对应的模糊关系矩阵
t=mhdj(r);
le=t-r;
while all(all(le==0)==0)==1 %如果t与r相等,则继续求r乘以r
r=t;
t=mhdj(r);
le=t-r;
end
disp('模糊等价矩阵为:')
t
for i=1:n
k=1;
for j=1:n
if t(i,j)>=lamda
group(i,k)=j;
k=k+1;
end
end
end
disp('聚类结果如下(数字0为自动填充数据,不是样本序号):')
group(1,:)
for i=2:n
k=0;
for j=1:i-1
if all(group(i,:)==group(j,:))==1 %两行值完全相等,不输出
k=1;break;
end
end
if k==0
disp(group(i,:)) %仅输出不重复的分类
end
end
mhdj.m
% 求模糊等价矩阵
function r_d=mhdj(r)
[m,n]=size(r);
for i=1:n
for j=1:n
for k=1:n
r1(i,j,k)=min(r(i,k),r(k,j));
end
r1max(i,j)=r1(i,j,1);
end
end
for i=1:n
for j=1:n
for k=1:n
if r1(i,j,k)>r1max(i,j)
r1max(i,j)=r1(i,j,k);
end
end
r_d(i,j)=r1max(i,j);
end
end
fuz_hc.m
function c=fuz_hc(a,b)
%模糊矩阵的合成运算程序
%输入模糊矩阵a,b,输出合成运算结果c
m=size(a,1);n=size(b,2);p=size(a,2);
%错误排除
if size(a,2)~=size(b,1)
disp('输入数据错误!');return;
end
%合成运算
for i=1:m
for j=1:n
for k=1:p
temp(k)=min(a(i,k),b(k,j));
end
c(i,j)=max(temp);
end
end
disp('模糊矩阵a与b作合成运算后结果矩阵c为:');
c
2.直接调用Matlab函数实现
2.1调用函数
层次聚类法(Hierarchical Clustering)的计算步骤:
①计算n个样本两两间的距离{dij},记D
②构造n个类,每个类只包含一个样本;
③合并距离最近的两类为一新类;
④计算新类与当前各类的距离;若类的个数等于1,转到5);否则回3);
⑤画聚类图;
⑥决定类的个数和类;
Matlab软件对系统聚类法的实现(调用函数说明):
cluster 从连接输出(linkage)中创建聚类
clusterdata 从数据集合(x)中创建聚类
dendrogram 画系统树状图
linkage 连接数据集中的目标为二元群的层次树
pdist 计算数据集合中两两元素间的距离(向量)
squareform 将距离的输出向量形式定格为矩阵形式
zscore 对数据矩阵 X 进行标准化处理
各种命令解释
⑴ T = clusterdata(X, cutoff)
其中X为数据矩阵,cutoff是创建聚类的临界值。即表示欲分成几类。
以上语句等价与以下几句命令:
Y=pdist(X,’euclid’)
Z=linkage(Y,’single’)
T=cluster(Z,cutoff)
以上三组命令调用灵活,可以自由选择组合方法!
⑵ T = cluster(Z, cutoff)
从逐级聚类树中构造聚类,其中Z是由语句likage产生的(n-1)×3阶矩阵,cutoff是创建聚类的临界值。
⑶ Z = linkage(Y) Z = linkage(Y, ‘method’)
创建逐级聚类树,其中Y是由语句pdist产生的n(n-1)/2 阶向量,’method’表示用何方法,默认值是欧氏距离(single)。有’complete’——最长距离法;‘average’——类平均距离;‘centroid’——重心法 ;‘ward‘——递增平方和等。
⑷ Y = pdist(X) Y = pdist(X, ‘metric’)
计算数据集X中两两元素间的距离, ‘metric’表示使用特定的方法,有欧氏距离‘euclid’ 、标准欧氏距离‘SEuclid’ 、马氏距离‘mahal’、明可夫斯基距离‘Minkowski‘ 等。
⑸ H = dendrogram(Z) H = dendrogram(Z, p)
由likage产生的数据矩阵z画聚类树状图。P是结点数,默认值是30。
2.2举例说明
设某地区有八个观测点的数据,样本距离矩阵如表1所示,根据最短距离法聚类分析。
%最短距离法系统聚类分析
X=[7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.29;
7.68 50.37 11.35 13.3 19.25 14.59 2.75 14.87;
9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.76;
9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.35;
10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.81];
BX=zscore(X); % 标准化数据矩阵
Y=pdist(X) % 用欧氏距离计算两两之间的距离
D=squareform(Y) % 欧氏距离矩阵
Z = linkage(Y) % 最短距离法
T = cluster(Z,3) 等价于 {
T=clusterdata(X,3) }
find(T==3) % 第3类集合中的元素
[H,T]=dendrogram(Z) % 画聚类图
聚类谱系图如图1所示:
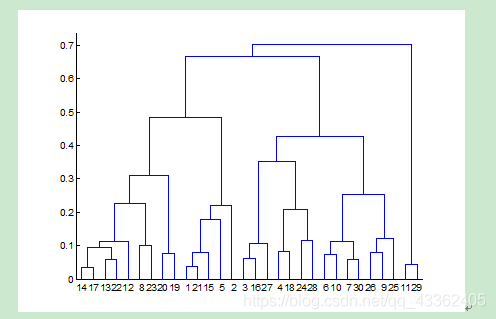
图1 聚类谱系图
3.用SPSS软件实现聚类分析
在SPSS软件中同样可以实现该算法,
例如:下表是1999年中国省、自治区的城市规模结构特征的一些数据,可通过聚类分析将这些省、自治区进行分类,具体过程如下:
省、自治区 首位城市规模(万人) 城市首位度 四城市指数 基尼系数 城市规模中位值(万人)
京津冀 699.70 1.437 1 0.936 4 0.780 4 10.880
山西 179.46 1.898 2 1.000 6 0.587 0 11.780
内蒙古 111.13 1.418 0 0.677 2 0.515 8 17.775
辽宁 389.60 1.918 2 0.854 1 0.576 2 26.320
吉林 211.34 1.788 0 1.079 8 0.456 9 19.705
黑龙江 259.00 2.305 9 0.341 7 0.507 6 23.480
苏沪 923.19 3.735 0 2.057 2 0.620 8 22.160
浙江 139.29 1.871 2 0.885 8 0.453 6 12.670
安徽 102.78 1.233 3 0.532 6 0.379 8 27.375
福建 108.50 1.729 1 0.932 5 0.468 7 11.120
江西 129.20 3.245 4 1.193 5 0.451 9 17.080
山东 173.35 1.001 8 0.429 6 0.450 3 21.215
河南 151.54 1.492 7 0.677 5 0.473 8 13.940
湖北 434.46 7.132 8 2.441 3 0.528 2 19.190
湖南 139.29 2.350 1 0.836 0 0.489 0 14.250
广东 336.54 3.540 7 1.386 3 0.402 0 22.195
广西 96.12 1.228 8 0.638 2 0.500 0 14.340
海南 45.43 2.191 5 0.864 8 0.413 6 8.730
川渝 365.01 1.680 1 1.148 6 0.572 0 18.615
云南 146.00 6.633 3 2.378 5 0.535 9 12.250
贵州 136.22 2.827 9 1.291 8 0.598 4 10.470
西藏 11.79 4.151 4 1.179 8 0.611 8 7.315
陕西 244.04 5.119 4 1.968 2 0.628 7 17.800
甘肃 145.49 4.751 5 1.936 6 0.580 6 11.650
青海 61.36 8.269 5 0.859 8 0.809 8 7.420
宁夏 47.60 1.507 8 0.958 7 0.484 3 9.730
新疆 128.67 3.853 5 1.621 6 0.490 1 14.470
(1)打开数据文件,在spss中可以打开多种类型的文件,如*.xls、.dbf、.txt、*.sav等,
File→Open→Data;
(2)进行聚类分析:Analyze→Classify→Hierarchical Cluster(此例子中用层次聚类法);

进入如下对话框,设置聚类变量,以及采用的聚类方法,是否显示聚类谱系图等(因为采用不同的聚类方法,分类结果不同)。
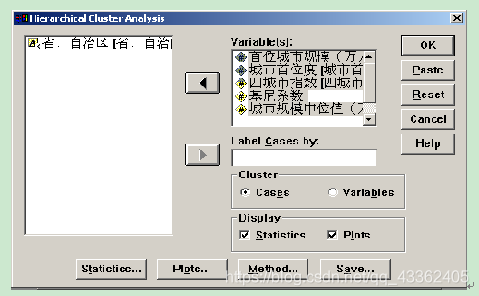
设置完成后,即可得到聚类结果,此例子中采用欧式距离计算样本之间各变量的距离,组平均法聚类,得到的聚类谱系图。