舵机的速度

 

■ 舵机的性能

---

舵机 在自动控制场合被广泛应用。舵机的输出力矩、转动速度、命令更新频率等标准了舵机的工作性能。在 全国大学生智能车竞赛中 ，大多数车模作品的方向控制都使用了舵机控制。在赛道上运行的车模速度，在 控制参数设置 合理的情况下，最高速度取决于舵机的响应速度。

通常，舵机的运行取决于 舵机特有的脉冲指令高电平时间宽度 ，而与脉冲指令的频率无关。所以控制舵机的脉冲波形与扫之电机运行的PWM波形的作用是不同的。

舵机内部具有驱动电路板，保证输出角度与脉冲指令的宽度之间呈现比例关系。舵机输出转角速度则取决于舵机本身内部机械结构、电机的性能、工作电压等各种因素。

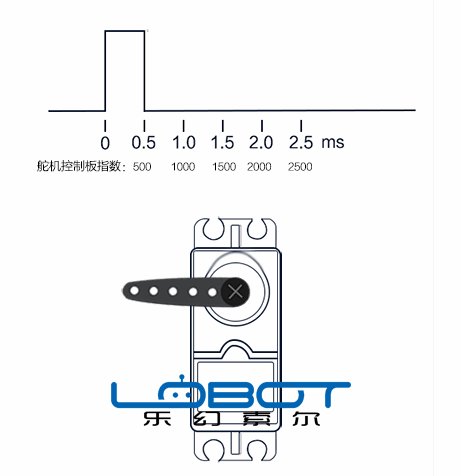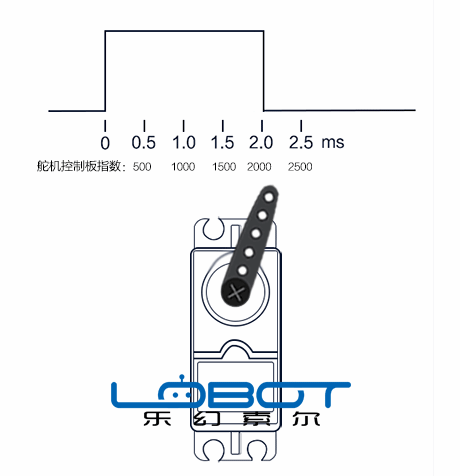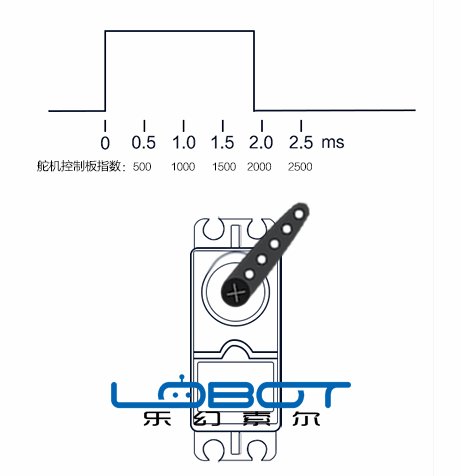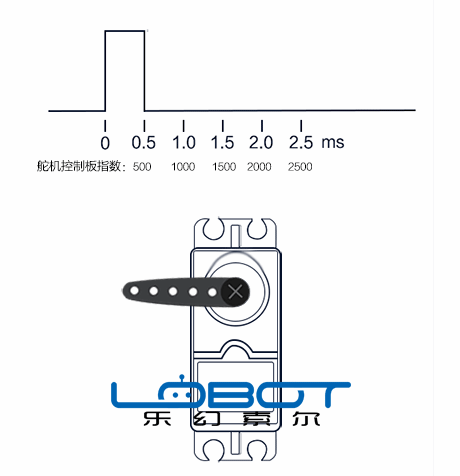
^{▲ 舵机指令与舵机转轴位置}

由于舵机的转速与指令无关，所以从本质上讲， 舵机不是一个线性模型 。当舵机转动角度越大，它的动态非线性就越明显。

 

01舵机转动速度与工作电压

---

舵机的转动速度越快，在智能车竞赛中车模控制性能就会越好。正好手边测试了一个 角度编码器 ST-3806-15-RS ，它有每周15bit的角度分辨率。这款角度编码器用于一款 双轴机械臂 的控制中。现在正好可以用它来测试舵机转动的角度、角速度。依次来分析舵机工作电压与执行速度之间的关系。

1.测量方法

选择S-D5舵机，使用橡胶套管将舵机输出轴与角度编码器连接在一起。使用机械平台将它们固定、共轴。使用 角度编码器 ST-3806-15-RS 测试电路模块来读取角度传感器的数值，控制多级的转动。

^{▲ 使用角度传感器测量舵机旋转速度}

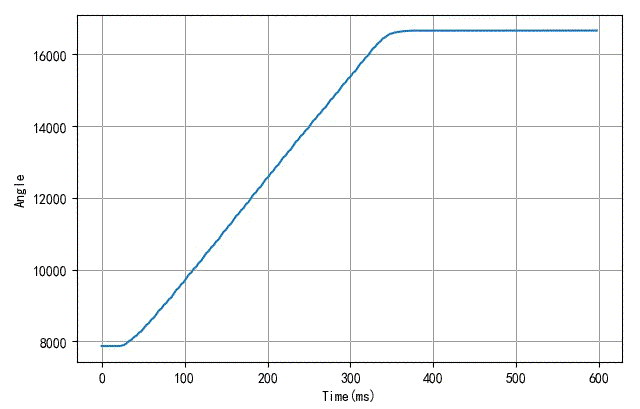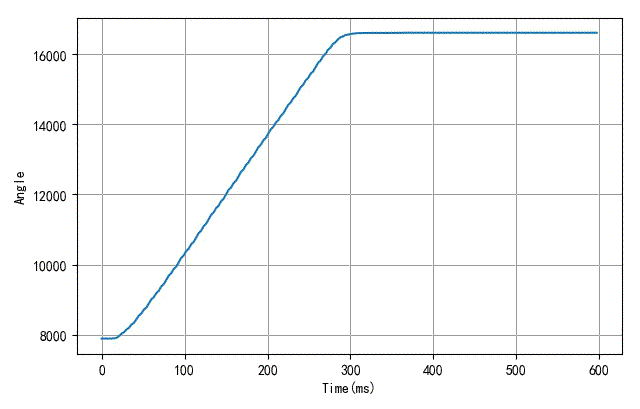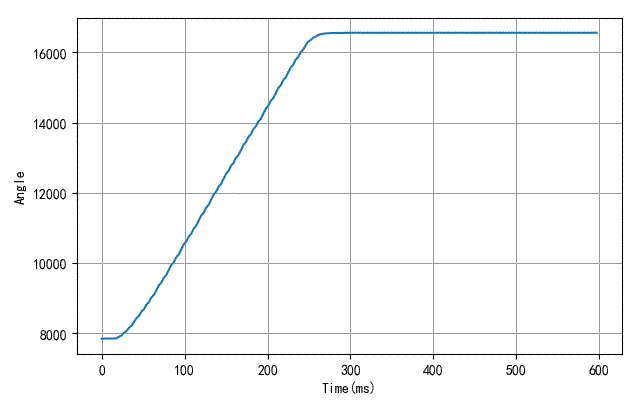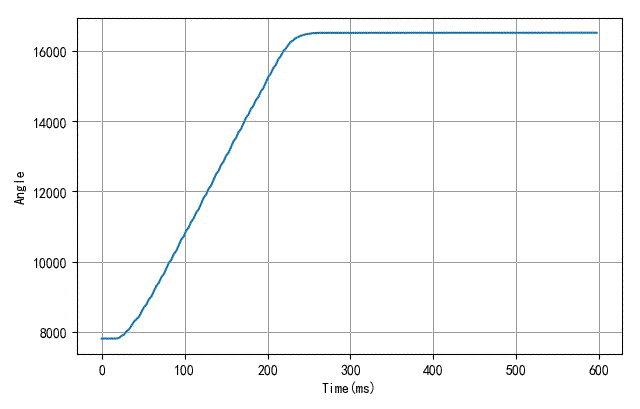
给定舵机脉冲指令，从1000us突变到2000us。舵机顺时针旋转60°。在这个过程中，采集角度的速率为3ms，读取200个。得到的角度曲线如下：

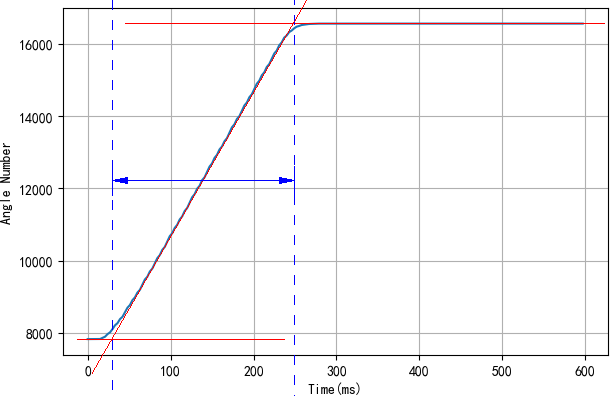
取角度上升线性部分（距离最下，最上各5%的余量），进行线性拟合。再计算拟合直线与最小角度、最大角度对应的时间交点。使用这个交点之间的时间差作为舵机的执行时间。执行时间的倒数可以反映舵机输出角速度。

^{▲ 测量旋转角度曲线对应执行时间}

2.测量数据

下面使用数控直流电源调节舵机工作电压，从4.0V ~ 6V，分成20个工作电压点。在每个工作电压点，测量舵机的转动曲线，使用上面的方法，获得舵机的转动时间。

^{▲ 随着工作电压的增加，舵机转动角度的曲线的变化}

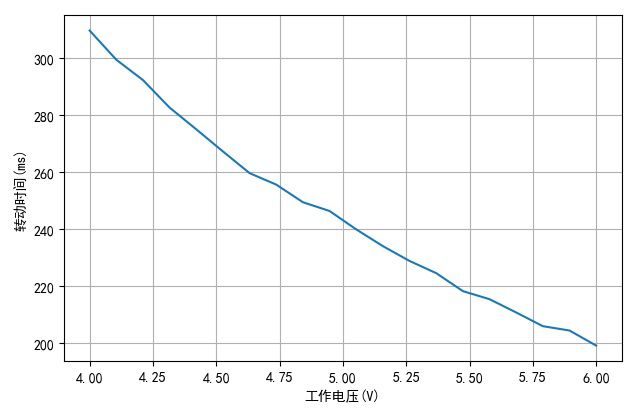
下图给出了舵机转动时间与工作电压测量的数据曲线。工作电压越高，舵机执行时间就越短。

^{▲ 工作电压与转动时间之间的关系}

voltagedim=[4.00,4.11,4.21,4.32,4.42,4.53,4.63,4.74,4.84,4.95,5.05,5.16,5.26,5.37,5.47,5.58,5.68,5.79,5.89,6.00]

timedim=[103.22,99.80,97.43,94.21,91.67,89.09,86.55,85.21,83.15,82.13,79.98,78.02,76.29,74.86,72.76,71.82,70.27,68.67,68.16,66.40]

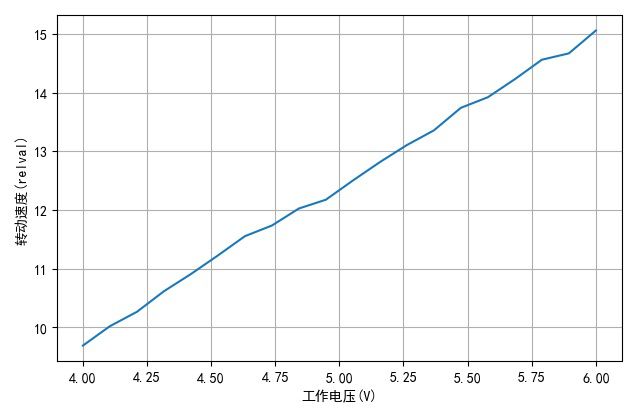
将上述时间取倒数（1000/time(ms)），可以获得下面的舵机转动相对速度与工作电压之间的关系。大体可以看到舵机执行速度与工作电压成正比。

^{▲ 工作电压与舵机转动速度之间的关系}

 

02分析结论

---

通过前面的分析可以看出：

• 为了提高多级的执行速度，可以在舵机允许的工作电压范围内尽可能提高舵机的工作电压；
• 为了避免高的工作电压对舵机内部的电路过压的影响，需要在舵机工作电源进行必要的限幅和稳压。
• 在舵机工作过程中，如果频繁的转动，需要考虑到舵机散热；

^{▲ 舵机指令在1000us在2000us之间切换变化}
此外，还可以通过在舵机输出轴，增加执行悬臂的长度，来通过机械放大提高舵机控制车模前轮转向的速度。

 

※ 测量代码

---

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY                     -- by Dr. ZhuoQing 2020-09-14
#
# Note:
#============================================================

from headm import *
from tsmodule.tsstm32       import *
from scipy.optimize         import curve_fit
from tsmodule.tsvisa        import *
from tsmodule.tsdraw        import *

dp1308open()

#------------------------------------------------------------

def linearf(x, a, b):
    return a*x+b

def ServoAngle():
    stm32cmd('CLEAR')
    stm32cmd('servoa')

    time.sleep(3)
    return stm32memo(1)

def rottime(angle):
    maxangle = max(angle)
    minangle = min(angle)
    timedim = linspace(0, len(angle) * 3, len(angle) * 3, endpoint=False)

    deltaangle = maxangle-minangle
    angle = array(angle)

    startangle = minangle + deltaangle * 0.05
    endangle = maxangle - deltaangle * 0.05

    startid = list(angle>startangle).index(True)
    endid = list(angle>endangle).index(True)

    angle1 = angle[startid:endid+1]
    time1 = timedim[startid:endid+1]

    param = (100, 0)
    param, conv = curve_fit(linearf, time1, angle1, p0=param)
    anglefit = linearf(time1, *param)

    starttime = (minangle - param[1]) / param[0]
    endtime = (maxangle - param[1]) / param[0]

    return endtime - starttime

#------------------------------------------------------------

setv = linspace(4, 6, 20)
timedim = []
voltagedim = []

pltgif = PlotGIF()

for v in setv:
    dp1308p6v(v)
    time.sleep(1)

    angle = ServoAngle()
    tspsave('sample1', angle=angle)
    rotatetime = rottime(angle)
    printf(rotatetime)

    voltagedim.append(v)
    timedim.append(rotatetime)

    tspsave('time', voltagedim = voltagedim, timedim=timedim)

    td = linspace(0, len(angle)*3, len(angle), endpoint=False)

    plt.clf()
    plt.plot(td, angle)
    plt.xlabel("Time(ms)")
    plt.ylabel("Angle")
    plt.grid(True)
    plt.tight_layout()
    plt.draw()
    plt.pause(.1)

    pltgif.append(plt)

dp1308p6v(5)
pltgif.save(r'd:\temp\1.gif')

printf('\a')

#------------------------------------------------------------
#        END OF FILE : TEST1.PY
#============================================================

 
■ 相关文献链接:

• S-D5舵机拆开看一看
• 全国智能车竞赛的“变”中有“进”
• 方向控制中的动态比例值-P
• 舵机的脉冲指令的频率对于舵机运动影响
• 舵机建模仿真
• 角度编码器 ST-3806-15-RS
• 双轴机械臂位置闭环控制：STC8H1K28，42HS48EIS,BH32