矩阵分解SVD
《矩阵分解SVD》
本来是做了一个MobileNetV2中的关于ReLU的一个实验,大体用到的知识是对一个 n ∗ 2 n*2 n∗2 的矩阵通过 2 ∗ m 2*m 2∗m 的随机矩阵映射到 n ∗ m n*m n∗m ,经过ReLU函数后再映射回 n ∗ 2 n*2 n∗2 ,那么就需要求一个 2 ∗ m 2*m 2∗m 的随机矩阵的逆矩阵,就涉及到了广义逆矩阵、EVD、SVD的相关知识,考研复习的时候这种问题都非常熟练,但是现在却有点陌生了,确实要学而时习之啊。
Key Words:线性代数基础、特征值、特征向量、广义矩阵的逆、SVD
Beijing, 2020
作者:RaySue
Agile Pioneer
文章目录
-
- 线性代数基础
-
- 特征值与特征向量
- 矩阵的逆
- 正交矩阵
- 奇异矩阵
- 广义逆矩阵
- 特征值分解 EVD
- 奇异值分解(Singular value decompositon,SVD)
-
- 左奇异矩阵 U
- 右奇异矩阵 V
- 证明求U、V的合理性
- 求广义逆矩阵
- SVD的应用场景
-
- 数据压缩
- 总结&思考
- 附录
- 参考
线性代数基础
首先得先弄清矩阵的概念:一个矩阵代表的是一个线性变换规则,而一个矩阵的乘法运行代表的是一个变换;
特征值与特征向量
定义: 设 A A A为为数域 P P P上的线性空间V的一个线性变换,如果对于P中一数 λ \lambda λ,存在非零向量 ξ \xi ξ,使得下式成立,那么 λ \lambda λ称为 A A A的一个特征值,而 ξ \xi ξ称为 A A A的属于特征值 λ \lambda λ的一个特征向量
A ξ = λ ξ A \xi = \lambda \xi Aξ=λξ
计算一个线性变换 A A A的特征值与特征向量的方法可以分为以下两步:
-
求出A的特征多项式 ∣ λ E − A ∣ |λE−A| ∣λE−A∣在数域P的全部根(几重根就算几个),这些根就是A的全部特征值;
-
把所得的特征值逐个带入 A X = λ i X AX=λ_iX AX=λiX ,求出关于每个特征值的一组基础解系,也就是全部的线性无关的特征向量;
特征值与特征向量的意义
矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
特征向量是原始维度的线性组合,表示矩阵的方向。特征值表示对应方向上的大小。
矩阵的逆
定义: 设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵,记作 A − 1 A^{-1} A−1
A − 1 ∗ A = E A^{-1}*A=E A−1∗A=E
-
矩阵可逆的充要条件是矩阵行列式的值不为0 ( ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0)
-
我们把这种行列式不为0的矩阵称为是“非退化”的,如果是方阵,那也称之为是“非奇异”的。
-
与“非奇异”相对应的“奇异”矩阵则是数据挖掘,机器学习领域中非常重要的一个概念。
正交矩阵
定义: 指满足 A A T = E AA^T=E AAT=E 的矩阵A,其中E为单位矩阵。正交矩阵是欧式空间的叫法,在酉空间(即复数域上的欧式空间)叫酉矩阵。从定义也能看出正交矩阵有着很多特殊的性质:
- A 的各行(列)是单位向量且两两正交;
- A 在任意一组标准正交基下对应的线性变换为正交变换(即只旋转向量,却不改变向量之间的夹角和向量长度)
- ∣ A ∣ = ± 1 |A| = \pm 1 ∣A∣=±1
- A T = A − 1 A^T = A^{-1} AT=A−1 (比较重要)
奇异矩阵
定义: 异矩阵:奇异矩阵就是不满秩的方阵。
通过这个定义,就不难推出以下3点奇异矩阵的性质(记奇异矩阵为A):
-
既然A不满秩,那么|A|=0;
-
根据上面说的定理3,如果|A|=0,那么A一定是不可逆的。同理,非奇异矩阵则一定是可逆的;
-
根据线性方程组解的情况(唯一解,无穷多解以及无解)可知,齐次线性方程组AX=0有无穷多的解,而线性方程组AX=b有无穷多的解或者无解。
-
同理对于非奇异矩阵A′,齐次线性方程组A′X=0有且只有唯一零解,线性方程组A′X=b有唯一解。
广义逆矩阵
定义: 若A是奇异矩阵或长方阵,若X是满足 A X A = A AXA=A AXA=A的任意矩阵,那么我们称X为 A A A的广义逆矩阵,用 A g , A − , A 1 , A + A^g,A^−,A^1,A^+ Ag,A−,A1,A+等符号表示。当A为非奇异矩阵时,A的广义逆矩阵就是A的逆。
满足以下3个性质的广义逆矩阵 M M M称为A的M-P广义逆矩阵矩阵,记为A+
- AMA=A
- MAM=M
- AM与MA均为对称矩阵
实际上,若A是非奇异矩阵, A − 1 A^{-1} A−1也满足上面这3个性质。也就是说,M-P逆就是通常逆矩阵的推广。
广义逆矩阵的计算方法可以通过奇异值分解的过程来推导。
特征值分解 EVD
在介绍奇异值分解之前,先介绍特征值分解,学过线性代数的同学都知道,n阶方阵可以被特征分解为特征向量和特征值。
如果是对称矩阵还可以分解成标准形,所以可得到 A A A 的特征值分解(由于对称阵的特征向量两两正交,所以 Q Q Q 为正交阵,正交阵的逆矩阵等于其转置),特征值分解就是将一个矩阵分解成下面的形式:
A = Q ∗ Σ ∗ Q T A = Q * \Sigma * Q^T A=Q∗Σ∗QT
其中 Q 是这个矩阵A的特征向量组成的矩阵, Σ \Sigma Σ 是一个对角阵
奇异值分解(Singular value decompositon,SVD)
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵,那么如果我们要处理的矩阵不是方阵它能不能被分解呢?当然可以。分解的方法被称为奇异值分解,即SVD。
假设有一个普通的矩阵A(m*n),我们可以将A表示成如下形式:
A = U ∗ Σ ∗ V T A = U * \Sigma * V^T A=U∗Σ∗VT
其中U、V为正交矩阵,即 U U T = E UU^T=E UUT=E, V V T = E VV^T=E VVT=E, U U U称为左奇异矩阵, V V V称为右奇异矩阵, Σ \Sigma Σ仅在主对角线上有值,其他元素均为0,我们称之为奇异值,上面矩阵的维度分别为 U ∈ R m × m , Σ ∈ R m × n , V ∈ R n × n U \in R^{m \times m}, \space \Sigma \in R^{m \times n}, \space V \in R^{n \times n} U∈Rm×m, Σ∈Rm×n, V∈Rn×n。
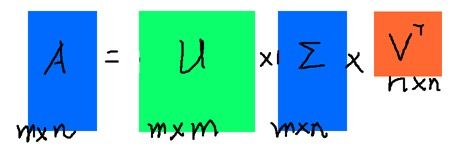
左奇异矩阵 U
左奇异矩阵U: A ∗ A T A*A^T A∗AT得到一个 m ∗ m m*m m∗m 的方阵,于是我们对 A ∗ A T A*A^T A∗AT进行特征值分解。即
( A A T ) u i = λ i u i (AA^T)u_i = \lambda_i u_i (AAT)ui=λiui
我们能得到m个特征值和对应的m个特征向量。m个向量组成特征向量矩阵U。
右奇异矩阵 V
右奇异矩阵V: A T ∗ A A^T*A AT∗A得到一个 n ∗ n n*n n∗n 的方阵,于是我们对 A T ∗ A A^T*A AT∗A 进行特征值分解。即
( A T A ) v i = λ i v i (A^TA)v_i = \lambda_i v_i (ATA)vi=λivi
我们能得到n个特征值和对应的n个特征向量。n个向量组成特征向量矩阵V
证明求U、V的合理性
A ∗ A T = U ∗ Σ ∗ V T ∗ V T ∗ Σ T ∗ U T = U ∗ Σ 2 ∗ U T A * A^T = U * \Sigma * V^T * V^T * \Sigma^T * U^T = U * \Sigma^2*U^T A∗AT=U∗Σ∗VT∗VT∗ΣT∗UT=U∗Σ2∗UT
同理
A T ∗ A = V ∗ Σ ∗ U T ∗ U ∗ Σ T ∗ V T = V ∗ Σ 2 ∗ V T A^T * A = V * \Sigma * U^T * U * \Sigma^T * V^T = V * \Sigma^2*V^T AT∗A=V∗Σ∗UT∗U∗ΣT∗VT=V∗Σ2∗VT
由上面的 特征值分解(EVD),可知 U U U为 A ∗ A T A * A^T A∗AT的特征值构成的矩阵, V V V为 A ∗ A T A * A^T A∗AT的特征值构成的矩阵, Σ \Sigma Σ 是 A ∗ A T A*A^T A∗AT的特征值的平方组成的对角阵。
求广义逆矩阵
由 A = U ∗ Σ ∗ V T ( 1 ) A = U * \Sigma * V^T \space\space (1) A=U∗Σ∗VT (1) 可得:
A g = ( U ∗ Σ ∗ V T ) g ( 2 ) A^g = (U * \Sigma * V^T)^g \space\space (2) Ag=(U∗Σ∗VT)g (2)
A g = ( Σ ∗ V T ) g ⋅ U T ( 3 ) A^g = (\Sigma * V^T)^g \cdot U^T \space\space (3) Ag=(Σ∗VT)g⋅UT (3)
A g = V ⋅ ( Σ ) g ⋅ U T ( 4 ) A^g = V \cdot (\Sigma )^g \cdot U^T \space\space (4) Ag=V⋅(Σ)g⋅UT (4)
其中, Σ \Sigma Σ 因为是对角阵,所以广义逆就是他所有元素的倒数。
SVD的应用场景
奇异值分解在机器学习中的用途非常广泛,例如图像去噪,降维,数据压缩方面的应用,另外还有潜在语义索引、推荐算法等。
数据压缩
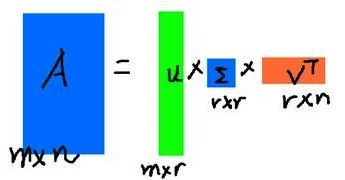
由于我们面对的数据大多是稀疏的数据,其内容本身很大,很占外存,但是其主要内容其实不是很多,我们就可以使用svd对数据进行压缩存储,比如一mxn的矩阵,我们利用svd分解后得到了mxm的U和mxn的 Σ \Sigma Σ以及nxn的V,我们可以根据奇异值的占比只取r (r < min(m,n))个奇异值,那么我们就可以用mxr,rxr,rxn的三个矩阵来存储原始的矩阵了。
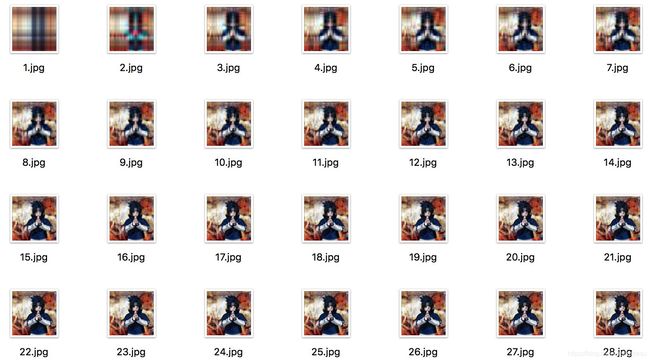
以图形压缩为例,下图的每个图像名称表示保存奇异值的个数重建得到的图,奇异值是从小到大排列的。
import numpy as np
import os.path as osp
import cv2
def restore_custom(sigma, u, v, K): # 奇异值、左特征向量、右特征向量
m = len(u)
n = len(v[0])
a = np.zeros((m, n))
for k in range(K):
a[k, k] = sigma[k]
a = u.dot(a).dot(v)
a = a.clip(0, 255)
return np.rint(a).astype('uint8')
if __name__ == "__main__":
A = cv2.imread('/Users/surui/back/zuozhu1.jpeg')
a = np.array(A)
print('type(a) = ', type(a))
print('原始图片大小:', a.shape)
u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0]) # 奇异值分解
u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1])
u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2])
save_dir = "./"
# # 使用前100个奇异值分解
K = 100
for k in range(1, K + 1):
print(k)
R = restore_custom(sigma_r, u_r, v_r, k)
G = restore_custom(sigma_g, u_g, v_g, k)
B = restore_custom(sigma_b, u_b, v_b, k)
I = np.stack((R, G, B), axis=2) # 合并
I = cv2.resize(I, (100, 100))
cv2.imwrite(osp.join(save_dir, str(k) + '.jpg'), I)
总结&思考
Q1: 为什么矩阵的特征值大的特征向量对应的信息较多?
A1: 首先矩阵就是一个代表的是方向和大小的向量,而特征向量是原始特征的线性组合,可以理解为一个新的基向量,而特征值是对应这个方向上的大小,那么在某个方向上越大,说明包含信息越多。
附录
基于python的svd的一种实现
def svd(X):
"""
先计算 右奇异矩阵 V,XTX,
再计算 左奇异矩阵 U XXT,
再根据 X = U * S * VT 计算出 S 即可,
S为对角矩阵
"""
# 求 V
V_sigma, V = np.linalg.eigh(X.T.dot(X))
V_sort_idx = np.argsort(V_sigma)[::-1]
V = V[:, V_sort_idx]
# 求 U
U_sigma, U = np.linalg.eigh(X.dot(X.T))
U_sort_idx = np.argsort(U_sigma)[::-1]
U = U[:, U_sort_idx]
# 已知U和V求S
S = U.T.dot(X).dot(V)
return U, S, V.T
参考
特征值和特征向量的意义
矩阵的分解:满秩分解和奇异值分解
奇异矩阵及广义逆矩阵
奇异值分解
主成分分析 PCA
numpy 求矩阵的特征值和特征向量
https://blog.csdn.net/guoziqing506/article/details/80557967