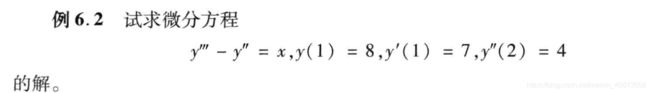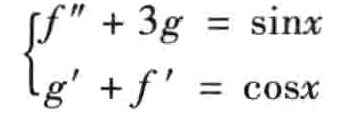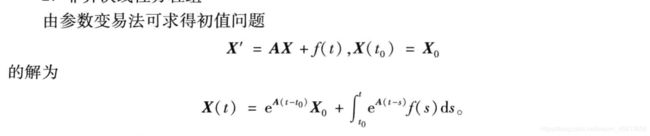2020年中国大学生数学建模竞赛备赛（十四）

微分方程符号解

MATLAB中符号运算工具箱

符号运算命令：$dsolve()$

[y1,...yN]=dsolve(eqns,conds,Name,Value);
//eqns为符号微分方程或符号微分方程组；conds为初值条件或者边值条件；Name和Value为可选的成对参数。

求常微分方程的通解

例题1：

clc,clear
syms y(x)//定义符号变量
dsolve(x^2+y+(x-2*y)

求解常微分方程的初边值问题

例题：

clc,clear
syms y(x)
dy=diff(y);d2y=diff(y,2);//定义一阶导数和二阶导数，用于初值或者边值条件的赋值
y=dsolve(diff(y,3)-diff(y,2)==x,y(1)==8,dy(1)==7,d2y(2)==4);
y=simplify(y);//把计算结果化简

求解常微分方程组

例题：试求常微分方程组：

的通解和在初值条件为$f^{\prime }(2)=0,f(3)=3,g(5)=1$的解

clc,clear
syms f(x) g(x)
df=diff(f);//定义f的一阶导数，用于初值或边值条件的赋值
[f1,g1]=dsolve(diff(f,2),+3*g==sin(x),diff(g)+df==cos(x));
f1=simplify(f1),g1=simplify(g1);
[f2,g2]=dsolve(diff(f,2)+3*g==sin(x),diff(g)+df==cos(x),df(2)==0,f(3)==3,g(5)==1);
f2=simplify(f2),g2=simplify(g2);

求解线性常微分方程组

1、一阶齐次线性微分方程组

例题：求解初值问题

clc,clear
syms x(t) y(t) z(t)
X=[x;y;z];
A=[2,1,3;0,2,-1;0,0,2];
B=[1,2,1]';
[x,y,z]=dsolve(diff(X)==A*X,X(0)==B);

2、非齐次线性方程组

例题：

clc,clear
syms x(t) y(t) z(t)
X=[x;y;z];A[1,0,0;2,1,-2;3,2,1];B=[0;0;exp(t)*cos(2*t)];
X0=[0;1;1];//初值条件
X=dsolve(diff(X)==A*X+B,X(0)==X0);//求符号解
X=simplify(X.x;X.y;X.z]);//显示解的各个分量
pretty(X);

应用举例

P116-P117 例6.6

clc,clear
syms g t(h)
t=dsolve(diff(t)==10000*pi/sqrt(2*g)*(h^(3/2)-2*h^(1/2)),t(1)==0);
t=simplify(t);
pretty(t);//分数线居中的显示方式

参考文献

司守奎，孙玺菁. 数学建模算法与应用. 北京：国防工业出版社，2011.