神经网络二值量化——ReActNet

本文为香港科技大学与卡内基·梅隆大学联合发表在ECCV2020。本文作者同系MetaPruning与Bi-RealNet的作者。本文基于二值网络训练精度低的问题，提出了三点优化，分别为重构二值网络结构，泛化传统的Sign和PReLU函数，分别表示为RSign和RPReLU和采用了一个分布损失来进一步强制二值网络学习类似于实值网络的输出分布。实验表明，在融合了所有技术后，所提出的 ReActNet 以很大的优势超越了之前所有的先进技术。

• 论文题目：ReActNet: Towards Precise Binary Neural Network with Generalized Activation Functions (ECCV2020)
• 论文链接：https://arxiv.org/abs/2003.03488
• 代码链接： https://github.com/liuzechun/ReActNet

摘要

本文提出了几种增强二值网络的想法，以缩小其与实值网络的精度差距，而不会产生任何额外的计算成本。首先通过修改和二值化一个紧凑的无参数的实值网络，绕过所有的中间卷积层（包括下采样层）来构建一个基线网络。该基线网络在精度和效率之间进行了很好的权衡，以近乎一半的计算成本实现了比现有大多数二进制网络更好的性能。通过大量的实验和分析，本文观察到二进制网络的性能对激活分布变化很敏感。基于这一重要的观察，本文提出了对传统的Sign和PReLU函数进行泛化，分别表示为RSign和RPReLU的泛化函数，以实现对分布重塑和偏移的显式学习，额外成本几乎为零。最后，本文采用了一个分布损失来进一步强制二值网络学习类似于实值网络的输出分布。实验表明，在融合了所有这些想法之后，所提出的 ReActNet 以很大的优势超越了之前所有的先进技术。具体来说，它在ImageNet数据集上的Top-1精度分别比 Real-to-Binary Net 和 MeliusNet29 高出 4.0% 和 3.6%，并且还将与实值网络的差距缩小到 3.0% 以内。

动机

在训练实值网络的过程中，对分布的重要性研究得并不多，因为随着权值和激活是连续的实值，重塑或移动分布将毫不费力。然而，对于 1-bit CNN 来说，学习分布既关键又困难。因为二元卷积中的激活只能从{-1,+1}中选取值，所以在符号函数之前，对输入的实值特征图做一个小小的分布移动，就有可能导致输出的二元激活完全不同，这将直接影响特征中的信息量，显著影响最终的精度。

为了说明问题，本文绘制了实值输入的输出二元特征图与原始（图3(b)）、正移（图3(a)）和负移（图3©）激活分布。实值特征图对偏移是稳健的，语义信息的可读性几乎可以保持，而二元特征图对这些偏移很敏感，如图3(a)和图3©所示。

方法

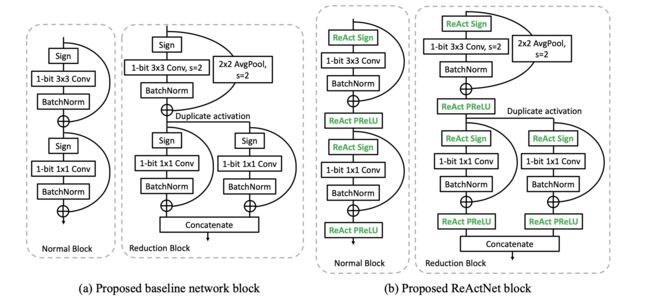
二值基准网络结构

泛化Sign和PReLU函数

基于上述动机中图3的观察，本文提出了一种简单而有效的操作来显式重塑和移动激活分布，称为 ReAct ，它将传统的 Sign 和 PReLU 函数分别泛化为 ReAct-Sign (缩写为RSign)和 ReAct-PReLU (缩写为RPReLU)，如下图所示：

图示&公式

• RSign公式如下所示：
  $$x_i^b=h\left(x_i^r\right)=\{\begin{array}{ll}+1,& \text{ if }{x}_i^r>{\alpha }_i\\ -1,& \text{ if }{x}_i^r\le {\alpha }_i\end{array}$$
  这里，$x_i^r$ 是第i个通道上RSign函数 h 的实值输入，$x_i^b$ 是二进制输出，${\alpha }_i$ 是控制阈值的可学习系数。${\alpha }_i$ 中的下标 i 表示不同通道的阈值可以不同。上标 b 和 r 表示二进制和实值。

• RPReLU公式如下所示：
  $$f\left(x_i\right)=\{\begin{array}{ll}{x}_i-{\gamma }_i+{\zeta }_i,& \text{ if }{x}_i>{\gamma }_i\\ {\beta }_i\left(x_i-{\gamma }_i\right)+{\zeta }_i,& \text{ if }{x}_i\le {\gamma }_i\end{array}$$
  其中 $x_i$ 是第i个通道上RPReLU函数 f 的输入，${\gamma }_i$ 和 ${\zeta }_i$ 是移动分布的可学习移位，${\beta }_i$ 是控制负部分斜率的可学习系数。各通道的系数都允许不同。

代码

主要是在 Sign 和 PReLU 前加入移位的bias。

class LearnableBias(nn.Module):
    def __init__(self, out_chn):
        super(LearnableBias, self).__init__()
        self.bias = nn.Parameter(torch.zeros(1,out_chn,1,1), requires_grad=True)

    def forward(self, x):
        out = x + self.bias.expand_as(x)
        return out

优化

• RSign梯度公式如下所示：
  $$\begin{array}{l}\frac{\partial \mathcal{L}}{\partial {\alpha }_i}={\sum }_{x_i^r}\frac{\partial \mathcal{L}}{\partial h\left(x_i^r\right)}\frac{\partial h\left(x_i^r\right)}{\partial {\alpha }_i}\\ \frac{\partial h\left(x_i^r\right)}{\partial {\alpha }_i}=-1\end{array}$$

• RPReLU梯度公式如下所示：
  $$\begin{array}{rl}\frac{\partial f\left(x_i\right)}{\partial {\beta }_i}& ={\mathbf{I}}_{\left\{x_i\le {\gamma }_i\right\}}\cdot \left(x-{\gamma }_i\right)\\ \frac{\partial f\left(x_i\right)}{\partial {\gamma }_i}& =-{\mathbf{I}}_{\left\{x_i\le {\gamma }_i\right\}}\cdot {\beta }_i-{\mathbf{I}}_{\left\{x_i>{\gamma }_i\right\}}\\ \frac{\partial f\left(x_i\right)}{\partial {\zeta }_i}& =1\end{array}$$

分布损失

公式

基于二值神经网络如果能够学习到与实值网络相似的分布，就可以提高性能的见解，本文使用分布损失来强制执行这种相似性，公式为：

$${\mathcal{L}}_{\text{Distribution }}=-\frac{1}{n}\sum _c\sum _{i=1}^n{p}_c^{{\mathcal{R}}_{\theta }}\left(X_i\right)\log \left(\frac{p_c^{{\mathcal{B}}_{\theta }}\left(X_i\right)}{p_c^{{\mathcal{R}}_{\theta }}\left(X_i\right)}\right)$$

其中，分布损失 ${\mathcal{L}}_{\text{Distribution }}$ 定义为实值网络 ${\mathcal{R}}_{\theta }$ 和二值网络 ${\mathcal{B}}_{\theta }$ 的 softmax 输出 $p_c$ 之间的KL散度。下标 c 表示类，n 为批次大小。

代码

class DistributionLoss(loss._Loss):
    """The KL-Divergence loss for the binary student model and real teacher output.

    output must be a pair of (model_output, real_output), both NxC tensors.
    The rows of real_output must all add up to one (probability scores);
    however, model_output must be the pre-softmax output of the network."""

    def forward(self, model_output, real_output):

        self.size_average = True

        # Target is ignored at training time. Loss is defined as KL divergence
        # between the model output and the refined labels.
        if real_output.requires_grad:
            raise ValueError("real network output should not require gradients.")

        model_output_log_prob = F.log_softmax(model_output, dim=1)
        real_output_soft = F.softmax(real_output, dim=1)
        del model_output, real_output

        # Loss is -dot(model_output_log_prob, real_output). Prepare tensors
        # for batch matrix multiplicatio
        real_output_soft = real_output_soft.unsqueeze(1)
        model_output_log_prob = model_output_log_prob.unsqueeze(2)

        # Compute the loss, and average/sum for the batch.
        cross_entropy_loss = -torch.bmm(real_output_soft, model_output_log_prob)
        if self.size_average:
             cross_entropy_loss = cross_entropy_loss.mean()
        else:
             cross_entropy_loss = cross_entropy_loss.sum()
        # Return a pair of (loss_output, model_output). Model output will be
        # used for top-1 and top-5 evaluation.
        # model_output_log_prob = model_output_log_prob.squeeze(2)
        return cross_entropy_loss

训练策略

文章采用两阶段训练策略，首先对激活进行二值，权重采用实数训练 256 Epochs；然后加载第一阶段得到的模型，进而对权重进行二值化处理，再训练 256 Epochs。

实验结果

消融实验

可视化

可学习的系数可视化

激活分布可视化

---