机器学习1——支持向量机（SVM）详细理论推导【图文版】

一、线性可分情况的支持向量机

1、引例

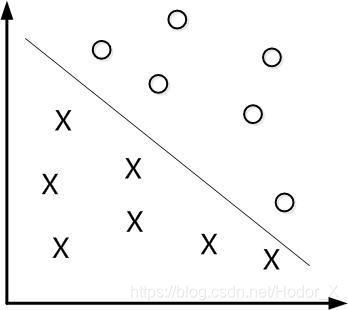
• 我们希望找到一条直线，来分开圆圈和叉。支持向量机 Support Vector Machine, SVM 是一种能够很好处理中等大小数据集的广义二元线性分类器。
• SVM属于监督学习 Supervised Learning 的一种，通过对带有标签 Label 的数据特征的学习，画出一条线、平面或者超平面 Hyper Plane 来分开不同的样本，即将每个样本分到不同的类，这样在给出一个新样本后，我们通过这个新样本的特征就可以判断它属于哪一类。
• SVM既可以用来做分类 Classification ，也可以用来做回归 Regression 。
• 如图，我们可以找到无数条线把这两种线性可分 Linearly Separable 的样本分开，但是我们希望找到一个最好的线，它可以容忍比较大的测量误差，提升整个模型的鲁棒性 Robustness。

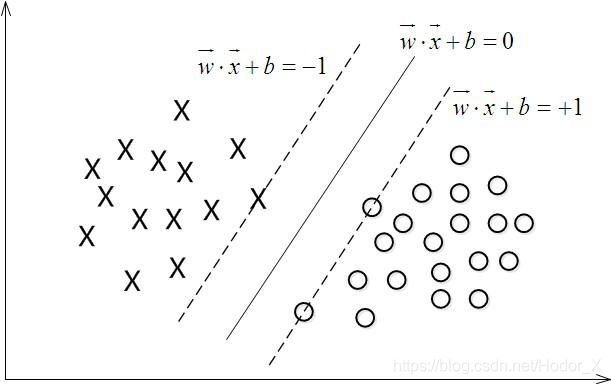
• 如何确定一条线的优劣程度需要有客观的评判标准，我们引入了几个概念。当你找到一条直线后，上下平行移动这条线，直到它擦过一个或者几个向量，我们将向上和向下两条直线的距离 $d$ 定义为这条直线的性能指标——间距 Margin，上下擦过的向量叫做支持向量 Support Vectors，那么SVM之所以好的原因就在于，它试图在找一条能够最大化间距的直线把样本分开，所以你也常常会听到人们说SVM是一个大间隔分类器 Large Margin Classifier。
  
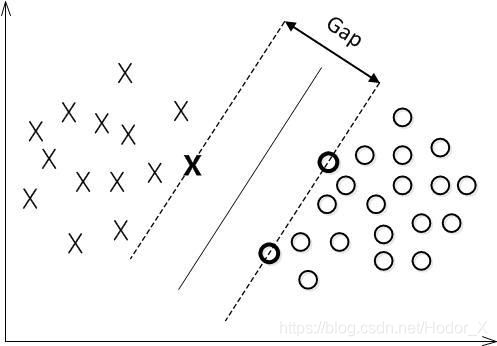
• 每确定一个间距 $d$，我们都会找到无数条满足这个间距的直线，我们选择与两边距离为 $\frac{d}{2}$ 的直线作为最后的边界。
• 细致观察后可以发现，支持向量机最后做出来的线只会与支持向量有关，与其他向量没有太大关系，且训练结束后支持向量占所有向量的比重不应该很大，如果占比过大，大概率是没有训练好，或者SVM无法将其线性分开。

---

2、定义

• 训练数据及标签：$$T=\left\{\left(X_1,y_1\right),\left(X_2,y_2\right),\dots ,\left(X_n,y_n\right)\right\}$$其中 $X_i$ 是向量，向量的维数即为特征的维数，
  标签 $y_i$ 的取值为离散值，为了推导方便，我们令其在这个二元分类问题上的取值为 $+1$ 和 $-1$
• 由参数 $W$ 和 $b$ 确定的超平面：$$W^T\cdot X+b=0$$ 这里的 $W$ 是与 $X$ 同维度的参数向量，
  $b$ 是一个常数
• 训练的过程就是确定参数 $W$ 和 $b$ 的过程，参数确定，平面找到，学习完成。
• 训练集线性可分的数学表达：
  $$训练样本T=\left\{\left(X_n,y_n\right)\right\}i=1\sim N$$$$\exists \left(W,b\right)使得对于\forall i=1\sim N都有:$$ $$a.若y_i=+1,则W^T\cdot X+b\ge 0$$ $$b.若y_i=-1,则W^T\cdot X+b\le 0$$当 $y_i$ 只取 $+1$ 和 $-1$ 时，可以将其简化为 $y_i\left(W^T\cdot X+b\right)\ge 0$

---

3、优化问题

寻找 $W$ 和 $b$，使得
最小化 Minimize： $\frac{1}{2}{\Vert W\Vert }^2$
限制条件 Subject to： $y_i\left(W^T\cdot X_i+b\right)\ge 1$    $i=1\sim N$

• 事实1： $W^T\cdot X+b\ge 0$ 和 $a{W}^T\cdot X+ab\ge 0$ 是同一个平面（$a\in \mathbb{R}$）
• 事实2：向量 $X_0$ 到超平面 $W^T\cdot X+b\ge 0$ 的距离为：$$d=\frac{W^T\cdot X_0+b}{\left|\left|W\right|\right|}$$

①综合两个事实，我们可以通过实数 $a$ 去缩放超平面方程，使得：$$\left(W,b\right)\to \left(aW,ab\right)$$②最终使得缩放后的 $W$ 和 $b$ 能够满足在所有的支持向量上：$$\left|W^T\cdot X_0+b\right|=1$$③将其带入事实2的公式中，可以得到支持向量与超平面的距离为 $\frac{1}{\Vert W\Vert }$，最大化距离就转化为最小化 $\Vert W\Vert$

• 对比上面的最小化内容，其中的 $\frac{1}{2}$ 仅仅是为了求导方便。
• 限制条件的这个 $1$ 其实可以是任意的常数，但是我们都可以通过缩放一个隐形的参数 $a$ 来将其调节为 $1$ ，之所以将这个作为了限制条件就是为了说对于每一次修改后的 $W$，和对于每一个需要满足等式为 $1$ 的支持向量，我们都可以找到一个对应的 $a$ 让其满足条件，所以我们只需不断地优化 $W$ 即可，无需担心每次优化后因为 $W$ 的改变而导致优化目标的改变，限制条件保证了参数 $a$ 在每一次的优化中其实都是在不停地改变自己从而平衡等式的值为 $1$，这个过程随时发生，虽然我们不需要求出 $a$ 的值，但正是因为 $a$ 有这个能力来变化自身，适应每次优化后的新参数值，才从而确保优化目标始终正确。
• 对于限制条件，$y_i$ 仅仅是一个常数，取值为 $+1$ 和 $-1$，因而可以忽略。对于除了支持向量之外的其他向量，将会有 $\left|W^T\cdot X_0+b\right|>1$，即距离更大，所以最后得出 $y_i\left(W^T\cdot X+b\right)\ge 1$ 的表达式。

---

4、得到凸优化中的二次规划问题

• 之所以SVM要这么做，转化我们的优化问题为这样的形式，实际上是因为它在尝试将其转化为凸优化中二次规划问题：
  ①目标函数为二次项     $\frac{1}{2}{\Vert W\Vert }^2$
  ②限制条件为一次项     $y_i\left(W^T\cdot X_i+b\right)\ge 1$    $i=1\sim N$
• 在上述的条件下，整个问题会变成一个凸优化问题，即要么无解，要么只有一个全局最优解，而不会出现局部极值的问题。
• 使用梯度下降等方法即可进行迭代，最终求解出参数 $W$ 和 $b$

---

二、线性不可分的处理方法

1、引例

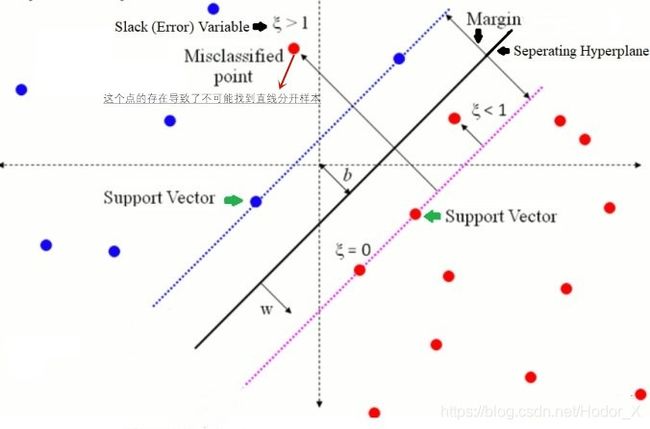
• 此时的SVM仍然试图用一个直线来分开样本，将会出现部分样本无法被正确划分，原来的限制条件也将不能满足。因而我们需要改变限制条件，从而使得能够满足现在的情况。

最小化 Minimize： $\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ （${\xi }_i$为松弛变量）
限制条件 Subject to：
$a.y_i\left(W^T\cdot X_i+b\right)\ge 1-{\xi }_i$    $i=1\sim N$
$b.{\xi }_i\ge 0$    $i=1\sim N$

• 我们引入了 ${\xi }_i$ 这个松弛变量，它的存在使得限制条件变得不那么严格了，尤其是当 ${\xi }_i$ 非常大的时候，限制条件 $a$ 式子会很容易成立，这是因为被正确分类的依然可以保证和线性可分一样的条件，满足其 $\ge 1$，但是对于那些被错误分配到另外一侧的，它的取值不过是加上了负号而已，可能是 $-10$，可能是 $-100$，但是我们也是能够找到最小的那个值，并且把 ${\xi }_i$ 设定得比那个值的绝对值更大，从而使得所有样本都成立。然而此时优化问题会变得非常发散，即可以想象对于一个线性不可分的问题，我们尝试使得所有样本都满足这个限制条件，最极限的时候即在无穷远处画线，所有样本归为一类，我们也能够满足条件。

• 因而我们在最小化目标的后面加上了这个正则项 $C{\sum }_{i=1}^N{\xi }_i$，通过参数 $C$ 来控制两项的权重，最小化 $\frac{1}{2}{\Vert W\Vert }^2$ 的同时限制 ${\xi }_i$ 的大小。

• 在优化问题中，$C$ 属于常数，$W$, $b$ , ${\xi }_i$（$i=1\sim N$）为待求解的变量。

• 修改后的优化问题对于线性不可分样本都能找到最优解，即它仍然是凸优化中的二次规划问题，保证了局部极值就是全局最小值。

• 当整个样本出现更加严重的非线性情况时：
  

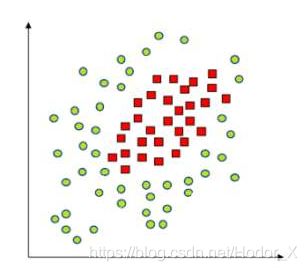
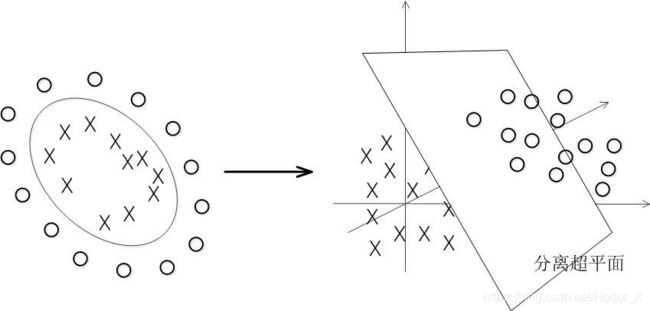
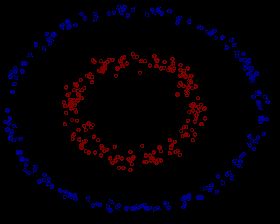
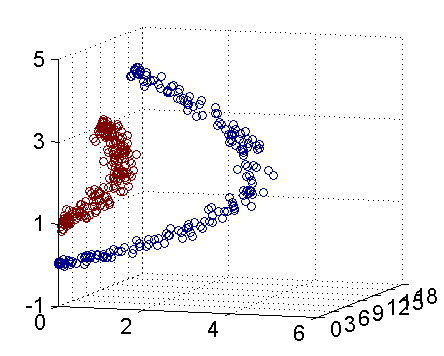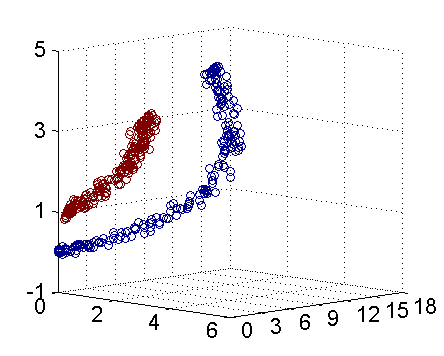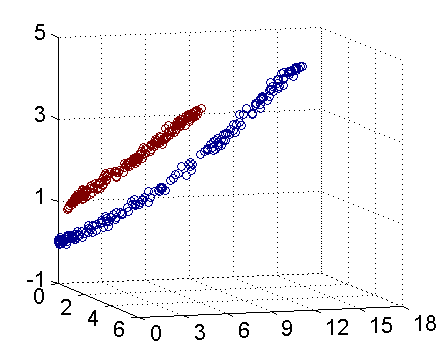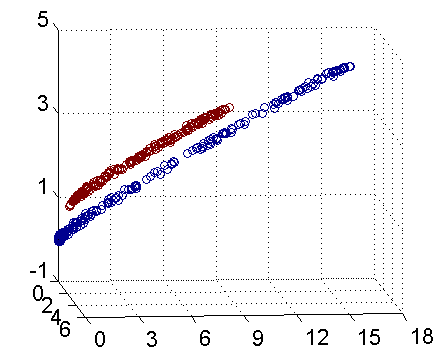
• 对于这些非线性情况，可以看到如果直接用直线进行拟合边界，最终效果会非常差。绝大多数算法会进而画出更加复杂的线，如椭圆，甚至更加不规则的线去拟合边界。而SVM的精髓在于它选择升维处理，对样本中所有点定义映射关系，将其投射到高维空间中，并在高维空间中寻找超平面分离样本，在低维空间线性不可分的数据集在高维空间中会有更大的几率被线性分开，当映射到无限维时，将样本线性分开的概率将为 $1$，其实化为简单的理解，如果我们对两个事物的更多特征有了了解，我们就更容易把他们分开，样本的维数就是样本的特征数。
  
  
  
  
  

---

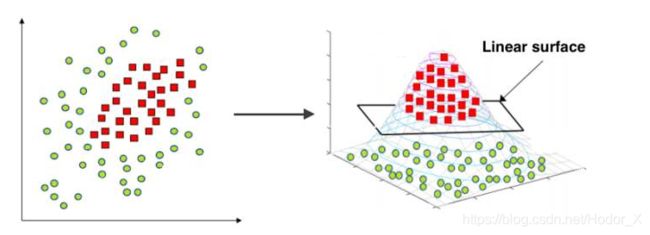
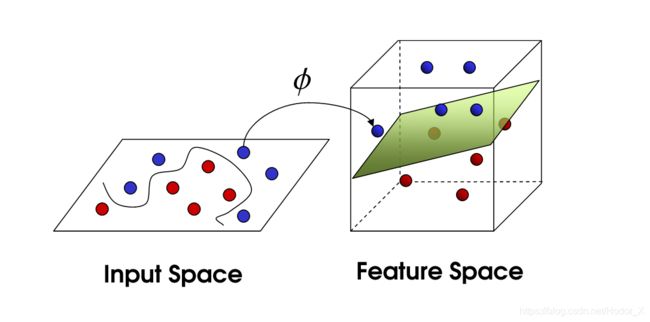
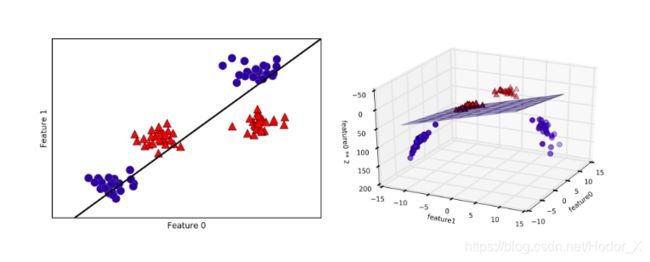
2、核函数来解决无限维的问题

• 当我们将 $X$ 通过 $\phi \left(x\right)$ 的映射关系映射到更高维度时，我们需要替换限制条件中的 $X_i$ 为 $\phi \left(X_i\right)$

最小化 Minimize： $\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ （${\xi }_i$为松弛变量）
限制条件 Subject to：
$a.y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\ge 1-{\xi }_i$    $i=1\sim N$
$b.{\xi }_i\ge 0$    $i=1\sim N$

• 然而正因为 $\phi \left(X_i\right)$ 是无限维，我们将无法知道 $\phi \left(x\right)$ 的显式表达式。此时创始人 Vapnik 指出，我们可以不用知道 $\phi \left(x\right)$ 的具体形式，取而代之对于空间中的任意向量，如果我们知道$$K\left(X_1,X_2\right)=\phi {\left(X_1\right)}^T\phi \left(X_2\right)$$我们就依然能够计算出 $W^T\cdot \phi \left(X\right)+b$ 的值，进而得出 $X$ 的所属类别。此时我们定义 $K\left(X_1,X_2\right)$ 为核函数 Kernel Function
• 核函数可以拆分成 $\phi {\left(X_1\right)}^T\phi \left(X_2\right)$ 的充要条件是Mercer’s Theorem（泛函分析）：
  ①$K\left(X_1,X_2\right)=K\left(X_2,X_1\right)$ （交换性）
  ②对于 $\forall C_i,X_i\left(i=1\sim N\right)$，有（半正定性）$$\sum _{i=1}^N\sum _{j=1}^N{C}_i{C}_j\ge 0$$
• 已被证实常用的核函数有：

1、线性核函数 Linear：$K\left(x,y\right)=x^{T}y$
用于线性可分的情况，参数少速度快，但其实使用线性核函数就是不使用核。

2、高斯径向基和函数 Radial Basis Function RBF：$K\left(x,y\right)=exp\left(-\frac{{||x-y||}^2}{2{\delta }^2}\right)$
参数少，性能较好，优先使用RBF。

3、多项式核函数 Polynomial：$K\left(x,y\right)=(a{x}^{T}y+c{)}^d$
属于有限维，性能较好，但是参数较多。

4、神经元核函数 Sigmoid：$K\left(x,y\right)=tanh(a{x}^{T}y+c)$
被大量用于深度学习的激活函数。

• 选取原则：
  ①特征数相对于样本数大很多，训练集的数据量不够支持我们训练一个复杂的非线性模型，应该选用逻辑回归模型或者不带核函数的SVM。
  ②特征数较小，在1-1000之间，样本数大小中等，在10-10000之间，使用高斯核函数的支持向量机。
  ③特征数较小，在1-1000之间，样本数较大，大于50000，使用SVM会特别慢，创造增加更多的特征，之后使用逻辑回归或者不带核的支持向量机。

---

3、原问题和对偶问题相关定理

• 通过原问题和对偶问题的转化，我们能够进一步改变优化目标的形式，最终结合核函数实现问题求解。
• 原问题 Prime Problem：

最小化 Minimize：$f\left(w\right)$
限制条件 Subject to: $$g_i\left(w\right)\le 0（i=1\sim K）$$ $$h_i\left(w\right)=0（i=1\sim M）$$

• 对偶问题 Dual Problem：

定义一个函数：$$L\left(w,\alpha ,\beta \right)=f\left(w\right)+\sum _{i=1}^K{\alpha }_i{g}_i\left(w\right)+\sum _{i=1}^M{\beta }_i{h}_i\left(w\right)$$ $$L\left(w,\alpha ,\beta \right)=f\left(w\right)+{\alpha }^{T}g\left(w\right)+{\beta }^{T}h\left(w\right)（均为列向量）$$
最大化 Maximize：$\theta \left(\alpha ,\beta \right)=\underset{所有定义域内的w}{\inf }L\left(w,\alpha ,\beta \right)$
在限定 $\alpha$ 和 $\beta$ 取值的情况下，去遍历所有的 $w$ ，对于所有的 $w$ 求得最小值。
接着在外层对于所有的 $\alpha$ 和 $\beta$ 求最大值。
限制条件 Subject to: ${\alpha }_i\ge 0（i=1\sim K）$

原问题与对偶问题的关系：如果 $w^{\ast }$ 是原问题的解，${\alpha }^{\ast }$ 和 ${\beta }^{\ast }$ 是对偶问题的解，则有 $f\left(w^{\ast }\right)\ge \theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)$
证明：$$\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)=\underset{所有定义域内的w}{\inf }L\left(w,{\alpha }^{\ast },{\beta }^{\ast }\right)\le L\left(w^{\ast },{\alpha }^{\ast },{\beta }^{\ast }\right)$$
即我们把对偶问题的解 ${\alpha }^{\ast }$ 和 ${\beta }^{\ast }$ 代进去，它右边一定会 $\le$ 原问题的解 $w^{\ast }$ 再带进去的值，因为 $inf$ 就是取所有 $w$ 取值代入后最小的值，而原问题的解代进去要么就是那个最小值取 $=$，要么就是比它大取 $>$，接着
$$L\left(w^{\ast },{\alpha }^{\ast },{\beta }^{\ast }\right)=f\left(w^{\ast }\right)+\underset{\ge 0}{{\alpha }^{\ast T}}\underset{\le 0}{g\left(w^{\ast }\right)}+{\beta }^{\ast T}\underset{=0}{h\left(w^{\ast }\right)}\le f\left(w^{\ast }\right)$$

原问题与对偶问题的间距 Duality Gap：$G=f\left(w^{\ast }\right)-\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)\ge 0$
G则被称作原问题与对偶问题的间距，对于某些特定的优化问题，我们可以证明：$G=0$

强对偶定理：
若 $f\left(w\right)$ 为凸函数：$$凸函数定义为：对\forall w_1,w_2,$$ $$f\left(\lambda w_1+\left(1-\lambda \right)w_2\right)\le \lambda f\left(w_1\right)+\left(1-\lambda \right)f\left(w_2\right)（\lambda \in [0,1]）$$
且 $g\left(w\right)=Aw+b，h\left(w\right)=Cw+d$，
则此优化问题的原问题和对偶问题间距为 $0$ ，即：$f\left(w^{\ast }\right)=\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)$

KKT条件：
在满足强对偶关系时，即满足 $f\left(w^{\ast }\right)=\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)$ 时，结合$$L\left(w^{\ast },{\alpha }^{\ast },{\beta }^{\ast }\right)=f\left(w^{\ast }\right)+\underset{\ge 0}{{\alpha }^{\ast T}}\underset{\le 0}{g\left(w^{\ast }\right)}+{\beta }^{\ast T}\underset{=0}{h\left(w^{\ast }\right)}\le f\left(w^{\ast }\right)$$
可以得知，对于 $\forall i=1\sim K$，要么 ${\alpha }_i^{\ast }=0$ ，要么$g_i^{\ast }=0$

---

4、原问题转化为对偶问题

• 我们需要求解的原问题：

最小化 Minimize： $\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ （${\xi }_i$为松弛变量）
限制条件 Subject to：
$a.y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\ge 1-{\xi }_i$    $i=1\sim N$
$b.{\xi }_i\ge 0$    $i=1\sim N$

• 对照标准原问题定义：

最小化 Minimize：$f\left(w\right)$
限制条件 Subject to: $$g_i\left(w\right)\le 0（i=1\sim K）$$ $$h_i\left(w\right)=0（i=1\sim M）$$

• 我们可以得到：
  ①$f\left(w\right)=\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$
  ②$g_1\left(w\right)$ 对应 $y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\ge 1-{\xi }_i$
  ③$g_2\left(w\right)$ 对应 ${\xi }_i\ge 0$

• 我们的 $f\left(w\right)$ 可以证明为凸函数，但是对比限制条件发现符号不一致，我们稍微进行修改：
  ①对所有的 ${\xi }_i$ 取反，使得 ${\xi }_i\le 0$
  ②为了保证优化问题不发生改变，对 $f\left(w\right)$ 也要变号：$f\left(w\right)=\frac{1}{2}{\Vert W\Vert }^2-C{\sum }_{i=1}^N{\xi }_i$
  ③同时限制条件 $a$ 经过变号移项后得到：$1+{\xi }_i-y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\le 0$

• 此时我们再次与原问题标准定义对比，$g\left(w\right)$ 对应着两个限制条件，没有 $h\left(w\right)$：
  ①$f\left(w\right)=\frac{1}{2}{\Vert W\Vert }^2-C{\sum }_{i=1}^N{\xi }_i$
  ②$g_1\left(w\right)\le 0$ 对应 $1+{\xi }_i-y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\le 0$
  ③$g_2\left(w\right)\le 0$ 对应 ${\xi }_i\le 0$

• 将原问题代入对偶问题的表达式中展开：
  $$最大化：\theta \left(\alpha ,\beta \right)=\underset{所有定义域内的w}{\inf }L\left(w,\alpha ,\beta \right)$$$$L\left(w,\alpha ,\beta \right)=f\left(w\right)+\sum _{i=1}^K{\alpha }_i{g}_i\left(w\right)+\sum _{i=1}^M{\beta }_i{h}_i\left(w\right)$$ $$\{\begin{array}{l}f\left(w\right)=\frac{1}{2}{\Vert W\Vert }^2-C{\sum }_{i=1}^N{\xi }_i\\ \{\begin{array}{l}{g}_1\left(w\right)=1+{\xi }_i-y_i\left(W^T\cdot \phi \left(X_i\right)+b\right)\\ g_2\left(w\right)={\xi }_i\end{array}\end{array}$$

• 我们得到的是：
  $$最大化：\theta \left(\alpha ,\beta \right)=inf\left\{\frac{1}{2}{\Vert W\Vert }^2-C{\sum }_{i=1}^N{\xi }_i+{\sum }_{i=1}^N{\alpha }_i\left[1+{\xi }_i-y_i\cdot \left(W^T\cdot \phi \left(x_i\right)+b\right)\right]+{\sum }_{i=1}^N{\beta }_i{\xi }_i\right\}$$ $$限制条件为：{\alpha }_i\ge 0，{\beta }_i\ge 0（i=1\sim N）$$
  遍历所有的 $w,{\xi }_i,b$，$L\left(w,\alpha ,\beta \right)$中的 $\alpha$ 对应这里面的 $\alpha$ 和 $\beta$，这是因为 $\alpha$ 在 $L$ 中对应着不等式的部分，$\beta$ 在 $L$ 中对应着等式的部分，在这个优化问题中没有出现。

• 对原方程求偏导，偏导都为 $0$ 的点即为极值点：
  对于向量求导：$$\frac{\partial f}{\partial W}=\left[\frac{\partial f}{\partial W_i}\right]=\left[\begin{array}{c}\frac{\partial f}{\partial W_1}\\ ⋮\\ \frac{\partial f}{\partial W_N}\end{array}\right]（i=1\sim N）$$
  对 $w,{\xi }_i,b$ 三个参数求偏导：$$\frac{\partial L}{\partial w}=0\Rightarrow w-{\sum }_{i=1}^N{\alpha }_i{y}_i\phi \left(X_i\right)\Rightarrow w={\sum }_{i=1}^N{\alpha }_i{y}_i\phi \left(X_i\right)$$ $$\frac{\partial L}{\partial b}=0\Rightarrow -{\sum }_{i=1}^N{\alpha }_i{y}_i=0\Rightarrow {\sum }_{i=1}^N{\alpha }_i{y}_i=0$$ $$\frac{\partial L}{\partial {\xi }_i}=0\Rightarrow {\sum }_{i=1}^{N}C={\sum }_{i=1}^N{\alpha }_i+{\sum }_{i=1}^N{\beta }_i\Rightarrow C-{\alpha }_i-{\beta }_i=0（i=1\sim N）$$

• 将其得到的偏导为 $0$ 的表达式代入 $\theta \left(\alpha ,\beta \right)$ 中化简得到：
  $$\theta \left(\alpha ,\beta \right)={\sum }_{i=1}^N{\alpha }_i+\frac{1}{2}{\Vert W\Vert }^2-{\sum }_{i=1}^N{\alpha }_i{y}_i{W}^T\phi \left(X_i\right)$$其中：
  $$\frac{1}{2}{\Vert W\Vert }^2=\frac{1}{2}{W}^{T}W=\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\phi }^T\left(X_i\right)\phi \left(X_j\right)$$ ${\phi }^T\left(X_i\right)\phi \left(X_j\right)$正好是核函数 $K\left(X_i,X_j\right)$，消掉了 $\phi$
  对于另一项：
  $${\sum }_{i=1}^N{\alpha }_i{y}_i{W}^T\phi \left(X_i\right)={\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\phi }^T\left(X_i\right)\phi \left(X_j\right)$$这里恰好又一次出现核函数 $K\left(X_i,X_j\right)$，消掉了${\phi }^T\left(X_i\right)\phi \left(X_j\right)$

• 整理后代入 $\theta \left(\alpha ,\beta \right)$ 得到：
  $$最大化：\theta \left(\alpha \right)={\sum }_{i=1}^N{\alpha }_i+\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(X_i,X_j\right)$$ $$限制条件：①0\le \alpha \le C，②{\sum }_{i=1}^N{\alpha }_i{y}_i=0$$
  其中第一个限制条件结合了 ${\alpha }_i\ge 0$， ${\beta }_i\ge 0$ 以及 $C-{\alpha }_i-{\beta }_i=0$，第二个限制条件就是 $\frac{\partial L}{\partial b}=0$ 的结果。

• 将原问题整理到这个表达式之后，即可使用 $SMO$ 算法求解优化后的 $\alpha$ 参数，最终我们可以利用这个优化后的 $\alpha$ 结合核函数对新的样本进行分类。

---

• 巧妙避开求 $W$ 的过程：
  $$若样本线性可分，则对于\forall i=1\sim N都有:$$ $$a.若y_i=+1,则W^T\cdot X+b\ge 0$$ $$b.若y_i=-1,则W^T\cdot X+b\le 0$$
  这里将 $X$ 替换成 $\phi \left(X\right)$，则可得到：
  $$W^T\cdot \phi \left(X\right)={\sum }_{i=1}^N{\left[{\alpha }_i{y}_i\phi \left(X_i\right)\right]}^T\phi \left(X\right)={\sum }_{i=1}^N{\alpha }_i{y}_{i}K\left(X_i,X\right)$$
  此时即完成了避开对 $W$ 求解也能得到答案。

• 使用KKT条件求解 $b$：

对于 $\forall i=1\sim K$，要么 ${\alpha }_i^{\ast }=0$ ，要么$g_i^{\ast }=0$

在这个优化问题中：$$\theta \left(\alpha ,\beta \right)=inf\left\{\frac{1}{2}{\Vert W\Vert }^2-C{\sum }_{i=1}^N{\xi }_i+{\sum }_{i=1}^N{\alpha }_i\left[1+{\xi }_i-y_i\cdot \left(W^T\cdot \phi \left(x_i\right)+b\right)\right]+{\sum }_{i=1}^N{\beta }_i{\xi }_i\right\}$$遍历所有的 $w,{\xi }_i,b$，$L\left(w,\alpha ,\beta \right)$中的 $\alpha$ 对应这里面的 $\alpha$ 和 $\beta$，
我们可以得到：
①要么 ${\beta }_i=0$ ，要么 ${\xi }_i=0$
②要么 ${\alpha }_i=0$，要么 $1+{\xi }_i-y_i\cdot \left(W^T\cdot \phi \left(x_i\right)+b\right)=0$

任取一个 $0<{\alpha }_i<C$，得到一个 ${\beta }_i>0$（也可以取所有最后求 $b$ 平均值，这样更准确）
此时 ${\xi }_i=0$ 且 $1+{\xi }_i-y_i\cdot \left(W^T\cdot \phi \left(x_i\right)+b\right)=0$，
同时我们推导出来了 $W^T\cdot \phi \left(X\right)={\sum }_{i=1}^N{\left[{\alpha }_i{y}_i\phi \left(X_i\right)\right]}^T\phi \left(X\right)={\sum }_{i=1}^N{\alpha }_i{y}_{i}K\left(X_i,X\right)$，
代入其中，求解 $b$，得到 $$b=\frac{1-y_i{\sum }_{i=1}^N{\alpha }_i{y}_{i}K\left(X_i,X\right)}{y_i}$$
至此，推导结束。

• 在拿到一个新的测试样本 $X$ 时，我们通过计算核函数，进而可以计算出 $W$ 和 $b$，判决标准为 $$\{\begin{array}{l}X\in C_1,W^T+b⩾0（{\sum }_{i=1}^N{\alpha }^i{y}^{i}K\left(X_i,X\right)+b⩾0）\\ X\in C_2,W^T+b<0（{\sum }_{i=1}^N{\alpha }^i{y}^{i}K\left(X_i,X\right)+b<0）\end{array}$$

---

后记

支持向量机在深度学习大热之前，乃至于现在都是一种稳健的监督学习手段，在数据集大小适中的情况下可以达到非常优秀的分类效果，其背后的原因正是这一套复杂但漂亮的数学理论支撑。本人在浙江大学胡浩基老师的课程指导下，结合各大论坛博客的贴文，最终对SVM有了非常深刻的理解，所以特意整理出详细地推导过程，意图帮助更多的人深入理解这一监督学习手段。

参考资料和博客

参考笔记：机器学习笔记：支持向量机（SVM）详细推导以及sklearn.svm.SVC的简单简介
图片来源：支持向量机通俗导论（理解SVM的三层境界）
浙江大学-研究生机器学习课程-胡浩基-https://www.bilibili.com/video/BV1dJ411B7gh
Demo MathType 在线公式编辑器-Latex