QMF滤波器组设计(QMFB) matlab实现
QMF滤波器组简介
QMF即正交镜像滤波器组。用于子带信号分解为多个信号,从而降低信号带宽,分解后的各路信号通过各自的通道滤波。
- 大致流程为:
在分析滤波器一侧,输入信号被分为k个子频带信号 - 通过抽取降低频带利用率
- 在综合滤波器一侧,通过零内插值和带通滤波重建原来的信号。
此文用QMFB。即两通道正交镜像滤波器组为例进行设计。
QMFB设计
系统框图如下:

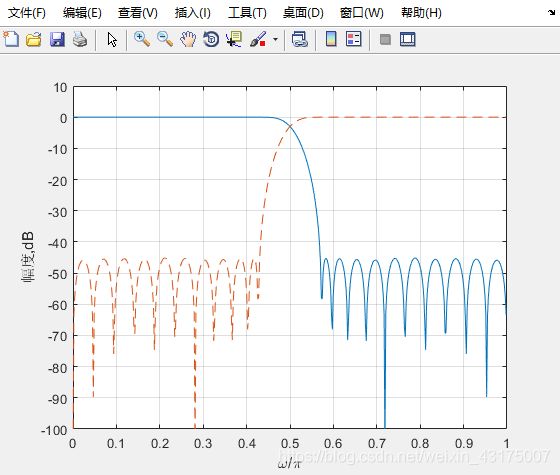
其中输入信号为x(n),分别被两个滤波器(低通和高通)分为两个子频带信号。两同通道信号分别进行2抽取,2插值后再通过带通滤波器后恢复为原来信号。
其中在QMFB中,两个滤波器有这样的关系:
∣ H 1 ( e j w ) ∣ = ∣ H 0 ( e j w + π ) ∣ H 1 ( z ) = H 0 ( − z ) h 1 ( n ) = ( − 1 ) n h 0 ( n ) |H_1(e^{jw})|=|H_0(e^{jw+\pi})|\\ H_1(z)=H_0(-z)\\ h_1(n)=(-1)^nh_0(n) ∣H1(ejw)∣=∣H0(ejw+π)∣H1(z)=H0(−z)h1(n)=(−1)nh0(n)
显示在频谱图中即为:
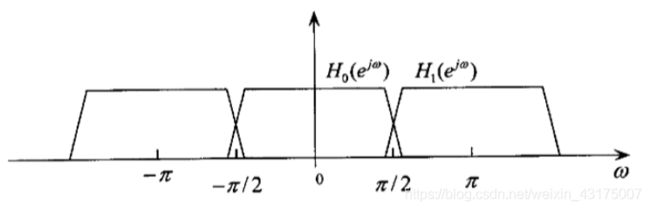
H0右移pi即可得到H1,同时pi/2就像一面镜子一样让两者对称,这也是QMF名字中“镜像”的由来。
重建端滤波器设计
由框图可得两通道信号的下采样值为:
X d 0 ( w ) = 1 2 ( X 0 ( w 2 ) + X 0 ( w + 2 π 2 ) ) X d 1 ( w ) = 1 2 ( X 1 ( w 2 ) + X 1 ( w + 2 π 2 ) ) X_{d0}(w)=\frac{1}{2}(X_0(\frac{w}{2})+X_0(\frac{w+2\pi}{2}))\\ X_{d1}(w)=\frac{1}{2}(X_1(\frac{w}{2})+X_1(\frac{w+2\pi}{2})) Xd0(w)=21(X0(2w)+X0(2w+2π))Xd1(w)=21(X1(2w)+X1(2w+2π))
两者再次经过上采样和带通滤波器后即可恢复原信号,输出波形为:
X ^ ( w ) = G 0 ( w ) X d 0 ( 2 w ) + G 1 ( w ) X d 1 ( 2 w ) = 1 2 ( G 0 ( w ) ( X 0 ( w ) ) + X 0 ( w − π ) ) + G 1 ( w ) ( X 1 ( w ) ) + X 1 ( w − π ) ) ) = 1 2 ( G 0 ( w ) H 0 ( w ) + G 1 ( w ) H 1 ( w ) ) X ( w ) + 1 2 ( G 0 ( w ) H 0 ( w − π ) + G 1 ( w ) H 1 ( w − π ) ) X ( w − π ) \hat{X}(w)=G_0(w)X_{d0}(2w)+G_1(w)X_{d1}(2w)\\ =\frac{1}{2}(G_0(w)(X_0(w))+X_0(w-\pi))+G_1(w)(X_1(w))+X_1(w-\pi)))\\ =\frac{1}{2}({G_0(w)H_0(w)+G_1(w)H_1(w)})X(w)+\\ \frac{1}{2}({G_0(w)H_0(w-\pi)+G_1(w)H_1(w-\pi)})X(w-\pi) X^(w)=G0(w)Xd0(2w)+G1(w)Xd1(2w)=21(G0(w)(X0(w))+X0(w−π))+G1(w)(X1(w))+X1(w−π)))=21(G0(w)H0(w)+G1(w)H1(w))X(w)+21(G0(w)H0(w−π)+G1(w)H1(w−π))X(w−π)
其中前半部分为理想输出波形,后半部分为理应去掉的混叠失真。
为此选择重建端的滤波器:
G 0 ( w ) = k H 1 ( w − π ) G 0 ( z ) = − k H 1 ( z ) = k H 0 ( z ) G 1 ( w ) = − k H 0 ( w − π ) G 1 ( z ) = k H 0 ( z ) = − k H 1 ( z ) G_0(w)=kH_1(w-\pi)\\ G_0(z)=-kH_1(z)=kH_0(z)\\ G_1(w)=-kH_0(w-\pi)\\ G_1(z)=kH_0(z)=-kH_1(z) G0(w)=kH1(w−π)G0(z)=−kH1(z)=kH0(z)G1(w)=−kH0(w−π)G1(z)=kH0(z)=−kH1(z)
此次重建中选择k=1,即
G 0 ( z ) = H 0 ( z ) G 1 ( z ) = − H 1 ( z ) G_0(z)=H_0(z)\\ G_1(z)=-H_1(z) G0(z)=H0(z)G1(z)=−H1(z)
输入端滤波器设计
和一般的滤波器设计一样,我们希望设计的滤波器通带尽量平,过渡带尽量窄,阻带衰减尽可能快。
即在QMFB中,对H0(w)和H1(w)的这方面性能要求很高。
当然理想的滤波器性能不可能实现,因此QMFB重建和其他重建一样,只能做到近似重建。
有以下三种方法选择:
- 用FIR QMF滤波器组,去除相位失真的前提下,尽可能的减小幅度失真,近似实现完全重建;
- 用IIR QMF滤波器组,去除幅度失真,不考虑相位失真,近似实现完全重建;
- 修正QMF滤波器 的关系,去考虑更合理的形式,从而实现完全重建。
本实验选择用FRI滤波器进行设计,即(1)。
相关参数选择
完全重建QMFB需要找到合适的N(滤波器阶数)和w(通带截至频率)的值,使得重建效果最好,即误差最小,且能获得良好的精度。
其中N一定为奇数,w要小于0.5.
确定方法为:先选定一个w,然后改变N的大小,求出不同情况下的MSE。选择最优情况时的N。
然后固定这个N,改变w,用同样的方法确定w。
最后通过实验确定了N=41,w=0.43.
matlab代码实现
不放处全部代码,只放出关键语句进行说明。
N=41;
w=0.43;
[h0,h1,g0,g1]=firpr2chfb(N,w);%Two-channel FIR filter bank for perfect reconstruction
firpr2chfb(N,w)是matlab信号处理工具箱自带函数,用于生成理想FIR双通道滤波器。
[H1z,w]=freqz(h0,1,512);%频响特性
H1_abs=abs(H1z);H1_db=20*log10(H1_abs);
[H2z,w]=freqz(h1,1,512);
H2_abs=abs(H2z);H2_db=20*log10(H2_abs);
sum1=H1_abs.*H1_abs+H2_abs.*H2_abs;
d=10*log10(sum1);%幅度相应关系误差
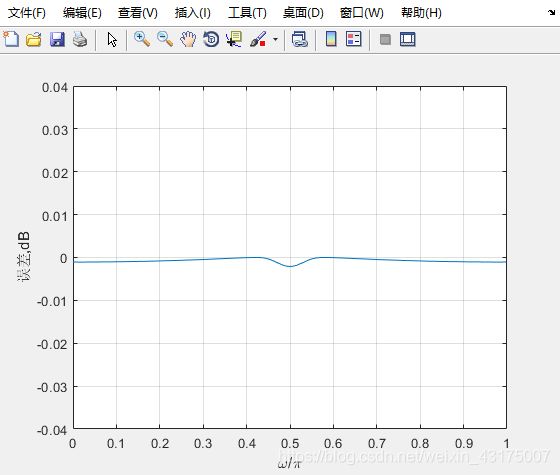
计算幅度相应关系误差的代码。
原理为:
10 l o g 10 ( ∣ H 1 ( e j w ) ∣ 2 + ∣ H 0 ( e j w + π ) ∣ 2 ) ≈ 0 10log_{10}(|H_1(e^{jw)}|^2+|H_0(e^{jw+\pi)}|^2)\approx0 10log10(∣H1(ejw)∣2+∣H0(ejw+π)∣2)≈0
本实验设置了三种输入信号:
%%%%%%%%%%%%%x1(n)%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(2)=1;x(3)=1;
x(6)=2;x(7)=2;x(8)=2;
x(17)=1.5;x(18)=1.5;x(19)=1.5;
x(24)=1;x(25)=1;
x(33)=3;x(34)=3;x(35)=3;
%%%%%%%%%%%%%%x2(n)%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(1)=1;x(2)=1;x(3)=1;
x(9)=2;x(10)=2;x(11)=2;
x(16)=3;x(17)=3;x(18)=3;
x(24)=4;x(25)=4;x(26)=4;
x(33)=3;x(34)=3;x(35)=3;
x(41)=2;x(42)=2;x(43)=2;
x(49)=1;x(50)=1;x(51)=1;
%%%%%%%%%%%%%%x3(n)%%%%%%%%%%%%%%%%%%%%
n=1:500;
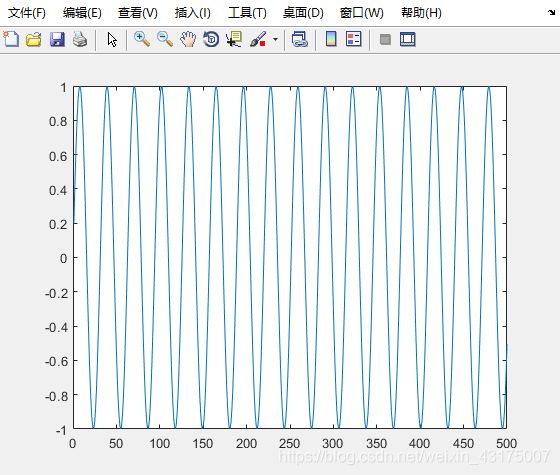
T=0.2;
x=sin(n*T);
下采样和上采样,以及对输入信号滤波并重建:
hlp=mfilt.firdecim(2,h0);%Direct-form FIR polyphase decimator抽取
hhp=mfilt.firdecim(2,h1);
glp=mfilt.firinterp(2,g0);%Direct-form FIR polyphase interpolator插值
ghp=mfilt.firinterp(2,g1);
x0=filter(hlp,x);
x0=filter(glp,x0);
x1=filter(hhp,x);
x1=filter(ghp,x1);
xidle=x0+x1;
xshift=[zeros(1,N) x(1:end-N)];
e=xidle-xshift;%误差值
mes=sum(abs(e).^2)/length(e)
fvtool(h0)
这里firdecim()和firinterp()分别为抽取和插值的函数。
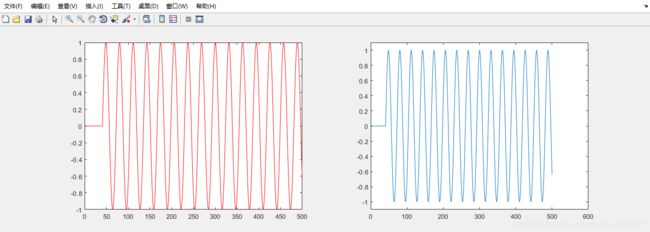
xidle为理想输出信号,e=xidle-xshift为重建误差值。MSE为均方误差。
代码中相关绘图部分略。
代码结果
输入端滤波器的幅度响应:
其中用fvtool绘制的H0的幅度响应为:
两者的幅度响应关系误差:
输入波形(选第三个):
理想输出波形(左)和重建波形(右):两者几乎没有区别,误差很小,重建效果不错:
两者的误差非常小,如下:
mes =
2.5899e-08