191007CSP-S模拟题解

博主来口胡联赛组巨佬们的考试题辣

T1：给一个序列，保证只有两个数出现了奇数次，求出这两个数
数据范围只允许$O(n)$
显然考虑出现奇数次的数字和出现偶数次的有什么不同，当然是全部异或起来后出现偶数次的全没了
所以先全部异或起来得到两个所求数的异或值，这个异或值某一位为1表示某个数这一位为1而另一个数这一位为0，那就把这一位为1的数再全部异或一遍就完了

Code：太傻逼不想写

T2：给出n个线性映射，支持实时修改，询问0依次进行所有映射的结果，$n\le 5e5$
线性映射。。。线段树维护矩阵乘法

Code：太傻逼不想写

T3：给一棵树，求加入一条边后使得所有点两两距离小于k的方案数，$n\le 2000$
这题真的是CSP难度吗。。。
考虑枚举这条边，显然我们要把检查的复杂度降到log以下
我们把一个端点作为根进行dfs，设另一个端点为y，深度为D
则我们可以把路径分为两类：与根到另一个端点的链（下文称为主链）相交的和不相交的（相交为边相交）
先考虑简单点的不相交的：
1.主链上每个节点不包含任何主链上的点的子树内的链，这种情况最长的为直径
2.主链上一个节点不包含任何主链上的点的子树内的一条通向这个节点的路径和另一个子树内的路径拼在一起，这种情况最长的为最大叶子，次大叶子，次次大叶子（以深度排序）中某两个拼在一起
那么这两种情况就比较好维护了
然后考虑相交的，我们设相交部分的端点为$u,v$,其中$v$是$u$的祖先，$l[x]$为主链上某个点往非主链节点能走到的最深位置，则有以下两种情况：

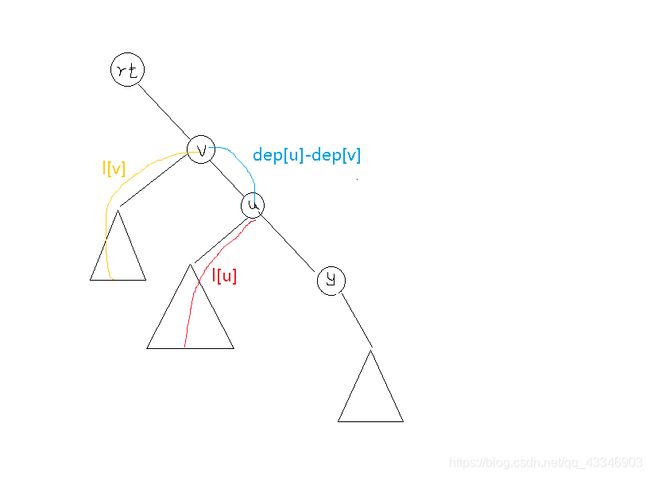
显然可以发现没有第三种情况了
则用不等关系表示出来就是下列两个不等式至少有一个要成立
$$l[u]+l[v]-dep[v]+dep[u]\le K$$
$$l[u]+l[v]+D-dep[u]+d[v]\le X\to l[u]+l[v]-dep[u]+dep[v]-K\ge D$$
那么显然就是以”不满足“第一个限制作为线段树的下标，查询第二个限制的最大值，看满不满足即可
注意dfs返回时要清空这次修改的影响

Source：TopCoder SRM 659 PublicTransitHard
Code：

#pragma GCC optimize(3)
#include
using namespace std;
inline int read(){
     
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) {
     if(ch=='-') f=-f;ch=getchar();}
	while(isdigit(ch)) {
     res=(res<<1)+(res<<3)+(ch^48);ch=getchar();}
	return res*f;
}
const int L=2000,N=2e3+5,INF=1e9;
int n,k;
namespace segtree{
     
	int tr[N<<4];
	#define mid (l+r>>1)
	inline void pushup(int k){
     tr[k]=max(tr[k<<1],tr[k<<1|1]);}
	int modify(int k,int l,int r,int pos,int val){
     
		if(l==r){
     int ret=tr[k];tr[k]=val;return ret;}
		int ret=0;
		if(pos<=mid) ret=modify(k<<1,l,mid,pos,val);
		else ret=modify(k<<1|1,mid+1,r,pos,val);
		pushup(k);return ret;
	}
	int query(int k,int l,int r,int ql,int qr){
     
		if(ql<=l && r<=qr) return tr[k];
		int mx=0;
		if(ql<=mid) mx=max(mx,query(k<<1,l,mid,ql,qr));
		if(qr>mid) mx=max(mx,query(k<<1|1,mid+1,r,ql,qr));
		return mx;
	}
	inline int modify(int pos,int v){
     pos+=L;return modify(1,1,n+L,pos,v);}
	inline int query(int ql,int qr){
     ql+=L,qr+=L;return query(1,1,n+L,ql,qr);}
}
using namespace segtree;
int l1[N],l2[N],l3[N];
int t1[N],t2[N];
int s1[N],s2[N];
int len[N];
int vis[N<<1],head[N],nxt[N<<1],tot=0;
inline void add(int x,int y){
     vis[++tot]=y;nxt[tot]=head[x];head[x]=tot;}
void dfs(int v,int fa){
     
	len[v]=s1[v]=s2[v]=t1[v]=t2[v]=l1[v]=l2[v]=l3[v]=0;
	for(int i=head[v];i;i=nxt[i]){
     
		int y=vis[i];
		if(y==fa) continue;
		dfs(y,v);
		len[v]=max(len[v],len[y]);
		if(len[y]>len[s1[v]]) s2[v]=s1[v],s1[v]=y;
		else if(len[y]>len[s2[v]]) s2[v]=y;
		int l=l1[y]+1;
		if(l>l1[v]) l3[v]=l2[v],l2[v]=l1[v],l1[v]=l,t2[v]=t1[v],t1[v]=y;
		else if(l>l2[v]) l3[v]=l2[v],l2[v]=l,t2[v]=y;
		else if(l>l3[v]) l3[v]=l;
	}
	len[v]=max(len[v],l1[v]+l2[v]);
}
int ans=0;
void dp(int v,int fa,int dep,int l){
     
	if(dep>l) return;
	int tmp=query(k-l1[v]-dep+1,n);
	if(len[v]<=k && k-l1[v]-tmp+1>=0) ++ans;
	for(int i=head[v];i;i=nxt[i]){
     
		int y=vis[i];
		if(y==fa) continue;
		int mx=y==s1[v]?len[s2[v]]:len[s1[v]];
		if(y==t1[v]) mx=max(mx,l2[v]+l3[v]);
		else if(y==t2[v]) mx=max(mx,l1[v]+l3[v]);
		else mx=max(mx,l1[v]+l2[v]);
		if(mx>k) continue;
		int L1=(y==t1[v])?l2[v]:l1[v];
		int tmp=query(k-L1-dep+1,n);
		if(tmp==0) tmp=-INF;
		tmp=k+dep+1-L1-tmp;
		int pre=modify(L1-dep,L1+dep);
		dp(y,v,dep+1,min(l,tmp));
		modify(L1-dep,pre);
	}
}
int main(){
     
	n=read();k=read();
	for(int x,i=2;i<=n;i++) x=read()+1,add(i,x),add(x,i);
	dfs(1,0);
	if(len[1]<=k) {
     cout<<n*(n+1)/2;return 0;}
	for(int i=1;i<=n;i++){
     if(i^1) dfs(i,0);dp(i,0,1,n);}
	cout<<(ans>>1);
	return 0;
}