PyTorch自用笔记(第四周)
PyTorch自用笔记(第四周)
- 七、神经网络与全连接层
-
- 7.1 逻辑斯蒂回归
- 7.2交叉熵
- 7.3 多分类问题实战
- 7.4 全连接层
-
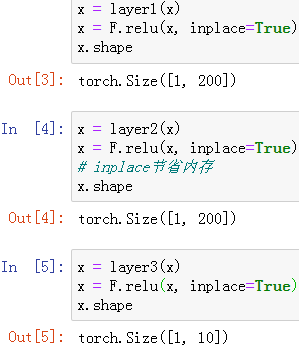
- `Linear操作`
- `ReLU激活`
- 自定义层次
- train
- 7.5 激活函数与GPU加速
- 7.6 Visdom可视化
- 八、实战技巧
-
- 8.1 过拟合与欠拟合
- 8.2 交叉验证
- 8.3 正则化
- 8.4 动量与学习率衰减
- 8.5 其他技巧
-
- early stopping
- dropout
- Stochastic Gradient Descent
- 九、卷积神经网络CNN
-
- 9.1 什么是卷积
- 9.2 卷积神经网络
- 9.3 池化层与采样层
- 9.4 标准化
-
- image normalization
- batch normalization
- 9.5 经典卷积网络
-
- LeNet-5
- AlexNet
- VGG
- GoogLeNet
- ResNet-最重要
- DenseNet
七、神经网络与全连接层
7.1 逻辑斯蒂回归
线性回归回顾:机器学习-吴恩达(第一周)二、模型描述
目标:pred = y
方法:最小化dist(|pred - y|)
逻辑斯蒂回归:机器学习-吴恩达(第二周)六、分类问题
目标:benchmark如精确度
方法1:最小化dist
方法2:最小化divergence
7.2交叉熵
softmax复习:
enlarger the larger
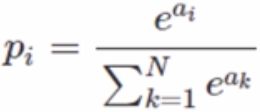
分类问题的loss:
1.MSE
2.Cross Entropy Loss(CEL)交叉熵
3.Hinge Loss(SVM常用)
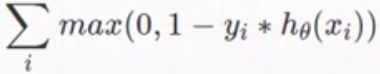
此处重点讨论交叉熵:
首先看一下entropy(熵)的概念:熵用来表示一种不稳定性(或稳定性);用来衡量惊喜程度;熵越高,信息越少,惊喜程度越小。
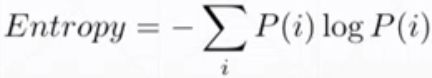
然后是Cross Entropy(交叉熵)的概念
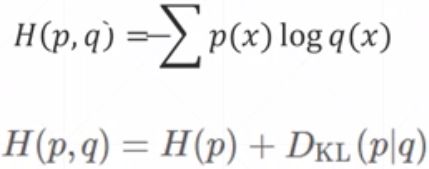
特殊情况:
1.P=Q,则H(p,q) = H§,即cross Entropy = Entropy
2.one-hot encoding,则Entropy = 1log1 = 0
对于二分类问题:
H(P,Q) = -(ylog§ + (1-y)log(1-p))
7.3 多分类问题实战
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
batch_size = 200
learning_rate = 0.01
epochs = 10
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
# 线性层 ch-out,ch-in;降维至200
w1, b1 = torch.randn(200, 784, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),\
torch.zeros(10, requires_grad=True)
# 初始化
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)
def forward(x):
x = x@w1.t() + b1
x = F.relu(x)
x = x@w2.t() + b2
x = F.relu(x)
x = x@w3.t() + b3
x = F.relu(x) # logits
return x
# 优化器
optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss() # softmax+log+nn.loss
for epoch in range(epochs):
for batch_idx, (data, target) in enumerate(train_loader):
data = data.view(-1, 28*28)
logits = forward(data)
loss = criteon(logits, target)
optimizer.zero_grad()
loss.backward()
# print(w1.grad.norm(), w2.grad.norm())
optimizer.step()
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
test_loss = 0
correct = 0
for data, target in test_loader:
data = data.view(-1, 28 * 28)
logits = forward(data)
test_loss += criteon(logits, target).item()
pred = logits.data.max(1)[1]
correct += pred.eq(target.data).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
运行结果:
E:\Anaconda\Anaconda3\python.exe E:/Python/PyTorch/main.py
Train Epoch: 0 [0/60000 (0%)] Loss: 2.516278
Train Epoch: 0 [20000/60000 (33%)] Loss: 0.795775
Train Epoch: 0 [40000/60000 (67%)] Loss: 0.566244
Test set: Average loss: 0.0242, Accuracy: 890/8952 (10%)
Train Epoch: 1 [0/60000 (0%)] Loss: 0.681463
Train Epoch: 1 [20000/60000 (33%)] Loss: 0.443154
Train Epoch: 1 [40000/60000 (67%)] Loss: 0.527179
Test set: Average loss: 0.0277, Accuracy: 882/8952 (10%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.614502
Train Epoch: 2 [20000/60000 (33%)] Loss: 0.688908
Train Epoch: 2 [40000/60000 (67%)] Loss: 0.558806
Test set: Average loss: 0.0298, Accuracy: 874/8952 (10%)
Train Epoch: 3 [0/60000 (0%)] Loss: 0.534761
Train Epoch: 3 [20000/60000 (33%)] Loss: 0.545937
Train Epoch: 3 [40000/60000 (67%)] Loss: 0.545407
Test set: Average loss: 0.0308, Accuracy: 883/8952 (10%)
Train Epoch: 4 [0/60000 (0%)] Loss: 0.383387
Train Epoch: 4 [20000/60000 (33%)] Loss: 0.402272
Train Epoch: 4 [40000/60000 (67%)] Loss: 0.417884
Test set: Average loss: 0.0316, Accuracy: 889/8952 (10%)
Train Epoch: 5 [0/60000 (0%)] Loss: 0.410931
Train Epoch: 5 [20000/60000 (33%)] Loss: 0.382123
Train Epoch: 5 [40000/60000 (67%)] Loss: 0.466876
Test set: Average loss: 0.0321, Accuracy: 886/8952 (10%)
Train Epoch: 6 [0/60000 (0%)] Loss: 0.426217
Train Epoch: 6 [20000/60000 (33%)] Loss: 0.377756
Train Epoch: 6 [40000/60000 (67%)] Loss: 0.471739
Test set: Average loss: 0.0332, Accuracy: 884/8952 (10%)
Train Epoch: 7 [0/60000 (0%)] Loss: 0.455824
Train Epoch: 7 [20000/60000 (33%)] Loss: 0.323968
Train Epoch: 7 [40000/60000 (67%)] Loss: 0.411355
Test set: Average loss: 0.0333, Accuracy: 887/8952 (10%)
Train Epoch: 8 [0/60000 (0%)] Loss: 0.347510
Train Epoch: 8 [20000/60000 (33%)] Loss: 0.394835
Train Epoch: 8 [40000/60000 (67%)] Loss: 0.308944
Test set: Average loss: 0.0340, Accuracy: 891/8952 (10%)
Train Epoch: 9 [0/60000 (0%)] Loss: 0.330805
Train Epoch: 9 [20000/60000 (33%)] Loss: 0.447674
Train Epoch: 9 [40000/60000 (67%)] Loss: 0.383535
Test set: Average loss: 0.0344, Accuracy: 883/8952 (10%)
注:初始化很重要,不同的初始值可以极大程度上影响学习结果
7.4 全连接层
Linear操作
ReLU激活
自定义层次
step1
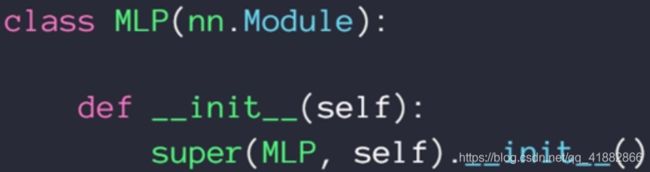
step2
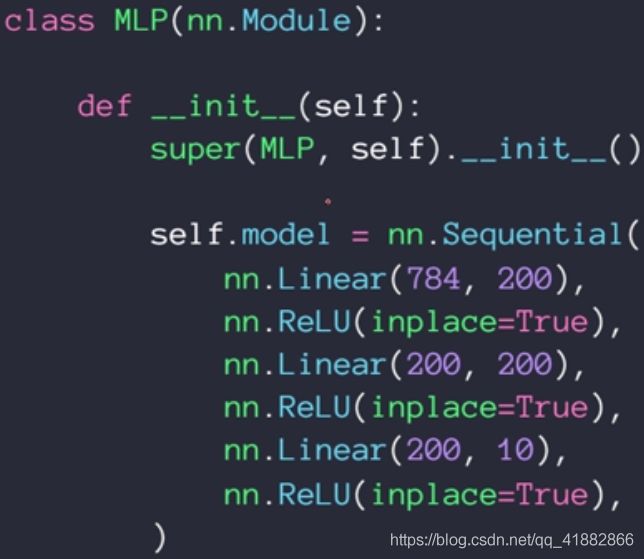
step3
MLP类内
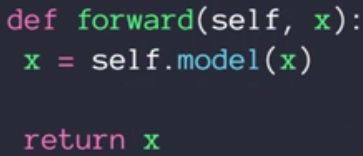
注:nn.ReLU vs F.relu()等价于类vs函数
train
7.5 激活函数与GPU加速
激活函数可见李飞飞计算机视觉-自用笔记(第二周)
7.6 Visdom可视化
下载并安装:pip install visdom
开启服务器:python -m visdom.server
此过程中如果出现Error404则需要重新手动安装
首先卸载:pip uninstall visdom
官网下载:github.com/facebookresearch/visdom
进入目录:cd Downloads;cd visdom-master
安装:pip install -e
回到用户目录运行python -m visdom.server
复制地址在浏览器打开
遇到问题:
启动visdom服务器时卡在downloading
解决方法:
找到visdom中的server.py,在最后几行的位置将download_scripts()注释掉,重新开启服务器,成功,将链接复制到浏览器打开即可
visdom示例
from visdom import Visdom
viz = Visdom() # viz实例
viz.line([0.], [0.], win='train_loss', opts=dict(title='train_loss')) # 初始[Y][X]=[0][0], win为ID,opts额外配置信息
viz.line([loss.item()], [global_step], win='train_loss', update='append')
八、实战技巧
8.1 过拟合与欠拟合
可见机器学习-吴恩达(第二周)7-1 过拟合问题
8.2 交叉验证
Train-Val-Test划分可参考机器学习-吴恩达(第四周)
7.3中的实战已经训练集和测试集的思想,即用训练集训练参数,每隔一段时间用测试集测试准确率;而实际中会用交叉验证集来测试准确率,在客户使用之前不会触碰测试集中的数据
50k:10k划分
print('train:', len(train_db), 'test:', len(test_db))
train_db, val_db = torch.utils.data.random_split(train_db, [50000, 10000])
print('db1:', len(train_db), 'db2:', len(val_db))
train_loader = torch.utils.data.DataLoader(
train_db,
batch_size=batch_size, shuffle=True)
val_loader = torch.utils.data.DataLoader(
val_db,
batch_size=batch_size, shuffle=True)
K-fold交叉验证集
比如60k的训练集,将其划分为N份,每次随机取N-1份做train,另外一份做交叉验证集
8.3 正则化
作用:改善过拟合
可参考机器学习-吴恩达(第四周)10-7
1.增加数据量
2.降低模型复杂度(shallow、正则化)
3.Dropout
4.数据增强
5.提前终结
本节讨论正则化的方法,L2也可叫权重衰减
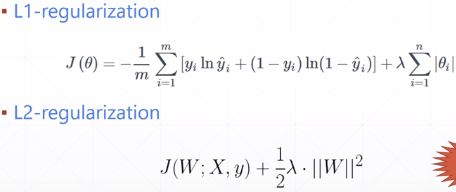
L2:(常用)
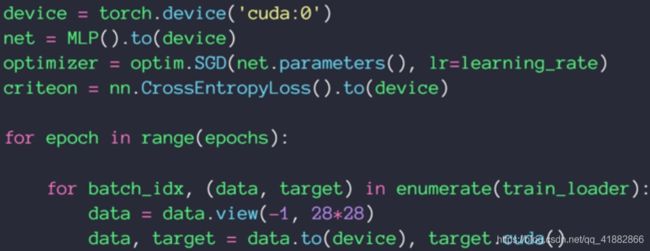
device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate, weight_decay=0.01)
criteon = nn.CrossEntropyLoss().to(device)
L1:
regularization_loss = 0
for param in model.parameters():
regularization_loss += torch.sum(torch.abs(param))
classify_loss = criteon(logits, target)
loss = classify_loss + 0.01 * regularization_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()
8.4 动量与学习率衰减
李飞飞计算机视觉-自用笔记(第三周)7
Scheme1
optimizer = torch.optim.SGD(model.parameters(), args.lr,
momentum=args.momentum,
weight_decay=args.weight_decay)
scheduler = ReduceLROnPlateau(optimizer, 'min') # 将优化器丢给函数管理;模式减少lr
for epoch in xrange(args.start_epoch, args.epochs):
train(train_loader, model, criterion, optimizer, epoch)
result_avg, loss_val = validate(val_loader, model, criterion, epoch)
scheduler.step(loss_val) # 监听loss
Scheme2
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 60
# lr = 0.0005 if 60 <= epoch < 90
# ...
scheduler = StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(100):
scheduler.step()
train(...)
validate(...)
8.5 其他技巧
early stopping
目的:防止过拟合
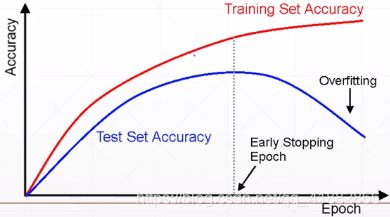
方法:
1.交叉验证集选择参数
2.检测验证集表现
3.在验证集表现最好时停止
dropout
李飞飞计算机视觉-自用笔记(第三周)7.2
net_dropped = torch.nn.Sequential(
torch.nn.Linear(784, 200),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(200, 200),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(200, 10),
)
注:测试时要取消dropout操作
for epoch in range(epochs):
# train
net_dropped.train()
for batch_idx, (data, target) in enumerate(train_loader):
...
net_dropped.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
...
Stochastic Gradient Descent
随机梯度下降 Stochastic != random
九、卷积神经网络CNN
9.1 什么是卷积
先导知识:
1.图像在计算机中以像素点形式存储,分为三个通道RGB
2.神经网络机器学习-吴恩达(第二周)机器学习-吴恩达(第三周)
3.人眼:感受野(局部相关性)
4.卷积核参数共享,大大减少了参数量
9.2 卷积神经网络
可参考李飞飞计算机视觉-自用笔记(第二周)
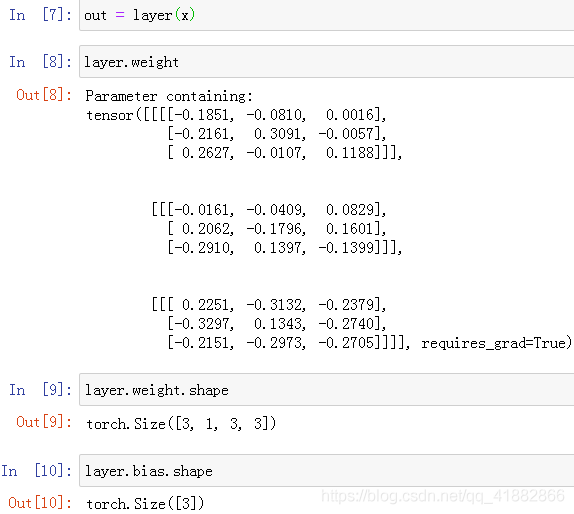
注:多个不同的kernel代表多个不同的观察图像的角度
input_channels:图像的通道
kernel_channels:卷积核的数量 | 对应input通道数量
kernel_size:卷积核的大小
stride:步长
padding:填充边界
bias:偏置;与kernel数量一致

特征学习:随着层次的叠加,从低维特征逐步过渡到高维特征
PyTorch中实现:
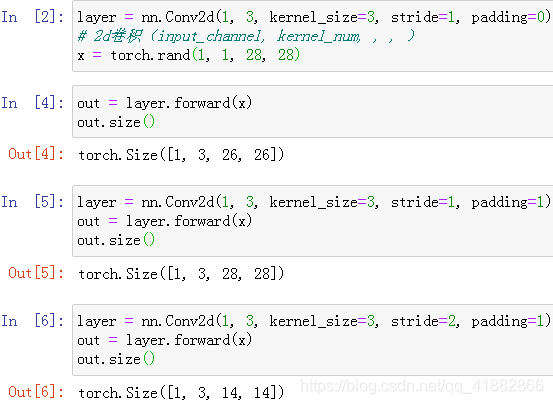
推荐将上过程直接写为:
out = layer(x) # __call__
9.3 池化层与采样层
下采样:隔行 | 隔列采样
最大池化(max pooling):
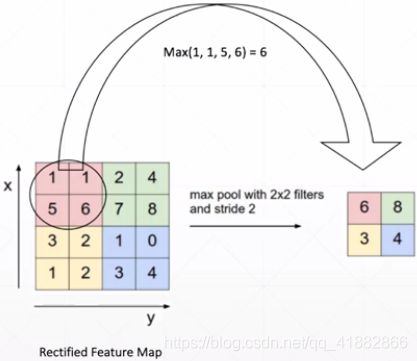
平均池化(avg pooling):取均值
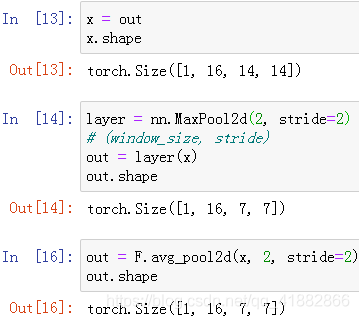
上采样:简单复制

ReLU:将图像只存在非负值

9.4 标准化
image normalization
在权值送到下一层之前,规范其符合高斯分布,方便梯度下降的快速进行
![]()
mean表示均值,std表示方差,三个值表示RGB三个通道,标准化过程就是用(X - μ)/ σ
batch normalization
training:
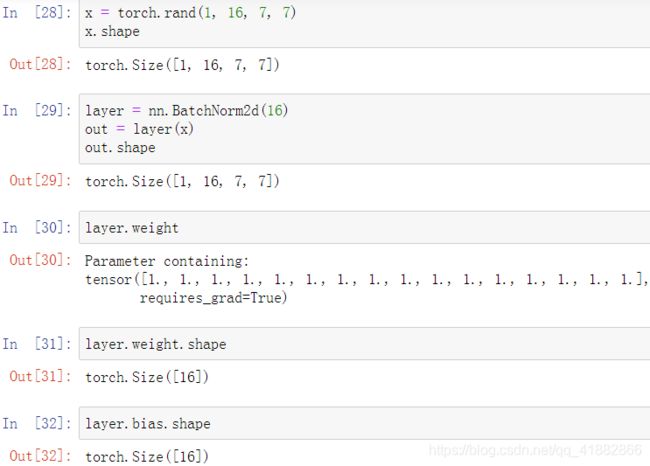
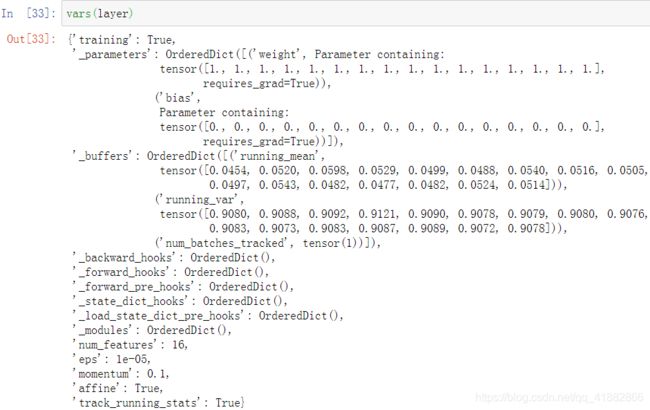
注:running_mean和running_var分别表示全局的均值和方差
test:
1.1个样本无法统计均值和方差
2.running_mean和running_var赋值给mean和var
3.无反向传播,不需更新

batch normalization优点:
1.收敛速度更快
2.更好搜索最优解
3.稳定性
9.5 经典卷积网络
可参考李飞飞计算机视觉-自用笔记(第四周),此处将会对之前学过的知识进行一个补充,已经出现过的内容不再赘述
LeNet-5
手写数字识别
3卷积+2全连接
AlexNet
5卷积+3全连接
VGG
VGG11
VGG16
VGG19
1 * 1卷积核
GoogLeNet
22层
ResNet-最重要
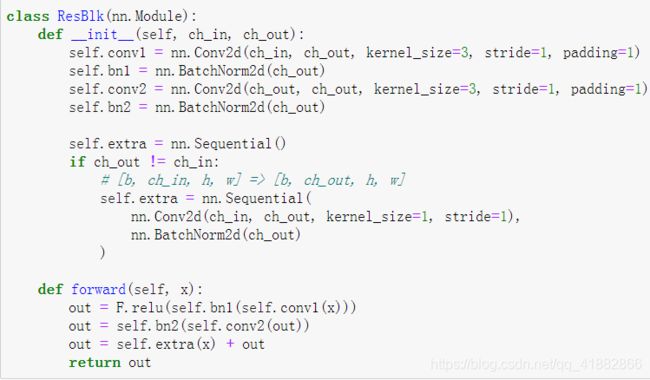
注:保证ch_in和ch_out即使不一致也可以做到残差相加
DenseNet
每一层与前面的所有层都有短接的存在