tensorflow画loss,acc曲线及数据保存
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time
import matplotlib.pyplot as plt
import numpy as np
x_data = tf.placeholder(tf.float32, [None, 784])
y_data = tf.placeholder(tf.float32, [None, 10])
x_image = tf.reshape(x_data, [-1, 28, 28, 1])
#convolve layer 1
filter1 = tf.Variable(tf.truncated_normal([5, 5, 1, 6]))
bias1 = tf.Variable(tf.truncated_normal([6]))
conv1 = tf.nn.conv2d(x_image, filter1, strides=[1, 1, 1, 1], padding=‘SAME’)
h_conv1 = tf.nn.sigmoid(conv1 + bias1)
maxPool2 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding=‘SAME’)
convolve layer 2
filter2 = tf.Variable(tf.truncated_normal([5, 5, 6, 16]))
bias2 = tf.Variable(tf.truncated_normal([16]))
conv2 = tf.nn.conv2d(maxPool2, filter2, strides=[1, 1, 1, 1], padding=‘SAME’)
h_conv2 = tf.nn.sigmoid(conv2 + bias2)
maxPool3 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding=‘SAME’)
convolve layer 3
filter3 = tf.Variable(tf.truncated_normal([5, 5, 16, 120]))
bias3 = tf.Variable(tf.truncated_normal([120]))
conv3 = tf.nn.conv2d(maxPool3, filter3, strides=[1, 1, 1, 1], padding=‘SAME’)
h_conv3 = tf.nn.sigmoid(conv3 + bias3)
full connection layer 1
W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 120, 80]))
b_fc1 = tf.Variable(tf.truncated_normal([80]))
h_pool2_flat = tf.reshape(h_conv3, [-1, 7 * 7 * 120])
h_fc1 = tf.nn.sigmoid(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
full connection layer 2
W_fc2 = tf.Variable(tf.truncated_normal([80, 10]))
b_fc2 = tf.Variable(tf.truncated_normal([10]))
y_model = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)
cross_entropy = - tf.reduce_sum(y_data * tf.log(y_model))
train_step = tf.train.GradientDescentOptimizer(1e-3).minimize(cross_entropy)
sess = tf.InteractiveSession()
correct_prediction = tf.equal(tf.argmax(y_data, 1), tf.argmax(y_model, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, “float”))
sess.run(tf.global_variables_initializer())
mnist = input_data.read_data_sets(“MNIST_data/”, one_hot=True)
fig_loss = np.zeros([1000])
fig_accuracy = np.zeros([1000])
start_time = time.time()
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(200)
if i % 100 == 0:
train_accuracy = sess.run(accuracy, feed_dict={x_data: batch_xs, y_data: batch_ys})
print(“step %d, train accuracy %g” % (i, train_accuracy))
end_time = time.time()
print(“time:”, (end_time - start_time))
start_time = end_time
print("********************************")
train_step.run(feed_dict={x_data: batch_xs, y_data: batch_ys})
**#训练完了可以打印出来或者保存到本地,后期可以继续使用
fig_loss[i] = sess.run(cross_entropy, feed_dict={x_data: batch_xs, y_data: batch_ys})
fig_accuracy[i] = sess.run(accuracy, feed_dict={x_data: batch_xs, y_data: batch_ys})
**print(fig_loss)
print(fig_accuracy)**
np.savetxt()
print(“test accuracy %g” % sess.run(accuracy, feed_dict={x_data: mnist.test.images, y_data: mnist.test.labels}))
绘制曲线
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
lns1 = ax1.plot(np.arange(1000), fig_loss, label=“Loss”)
按一定间隔显示实现方法
ax2.plot(200 * np.arange(len(fig_accuracy)), fig_accuracy, ‘r’)
lns2 = ax2.plot(np.arange(1000), fig_accuracy, ‘r’, label=“Accuracy”)
ax1.set_xlabel(‘iteration’)
ax1.set_ylabel(‘training loss’)
ax2.set_ylabel(‘training accuracy’)
合并图例
lns = lns1 + lns2
labels = [“Loss”, “Accuracy”]
labels = [l.get_label() for l in lns]
plt.legend(lns, labels, loc=7)
plt.show()
**
注:数据集保存在MNIST_data文件夹下
**
三步:
1)分别定义loss/accuracy一维数组
fig_loss = np.zeros([1000])
fig_accuracy = np.zeros([1000])
按间隔定义方式:fig_accuracy = np.zeros(int(np.ceil(iteration / interval)))
2)填充真实数据
fig_loss[i] = sess.run(cross_entropy, feed_dict={x_data: batch_xs, y_data: batch_ys})
fig_accuracy[i] = sess.run(accuracy, feed_dict={x_data: batch_xs, y_data: batch_ys})
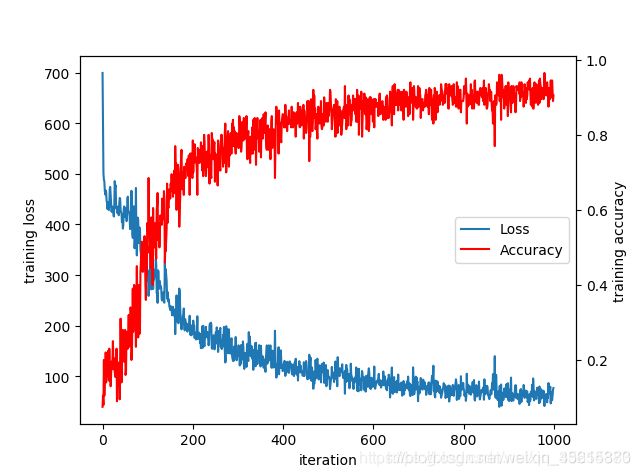
3)绘制曲线
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
lns1 = ax1.plot(np.arange(1000), fig_loss, label=“Loss”)
按一定间隔显示实现方法
ax2.plot(200 * np.arange(len(fig_accuracy)), fig_accuracy, ‘r’)
lns2 = ax2.plot(np.arange(1000), fig_accuracy, ‘r’, label=“Accuracy”)
ax1.set_xlabel(‘iteration’)
ax1.set_ylabel(‘training loss’)
ax2.set_ylabel(‘training accuracy’)
合并图例
lns = lns1 + lns2
labels = [“Loss”, “Accuracy”]
labels = [l.get_label() for l in lns]
plt.legend(lns, labels, loc=7)
————————————————
原文链接:https://blog.csdn.net/qq_33254870/article/details/81536188
问题:1.如何将array保存到txt文件中?2.如何将存到txt文件中的数据读出为ndarray类型?
需求:科学计算中,往往需要将运算结果(array类型)保存到本地,以便进行后续的数据分析。
解决:直接用numpy中的方法。
1:numpy.savetxt(fname,X):第一个参数为文件名,第二个参数为需要存的数组(一维或者二维)。
2.numpy.loadtxt(fname):将数据读出为array类型。

————————————————
原文链接:https://blog.csdn.net/kaever/article/details/61420696