2020力扣刷题

一、二维数组中的搜索

1、剑指4 && 力扣240

数组从左到右，从上到下升序排列。
思路：最快的方法是排除肯定不存在target的区域，从右上角的数开始比较。如果大于target，减列，如果小于target，加行。

2、力扣74

数组从左到右升序，下一行的第一个数大于上一行最后一个数
思路：一是直接采用二分算法，将原二维数组拉直，采用下标索引，直到找到target，在这个过程中，分清楚index和number值，遍历的是哪一个,行和列是怎么变化的；
二是利用剑指的思想，从行列的角度出发，排除不存在的区域，注意要判断数组是否为空，直接返回false。

二、括号

1、力扣20有效的括号

用到的数据结构
1、map< char,char > book;
book.insert(map::value_type(’)’,’(’));
2、stack< char > mystack;

mystack.empty()；
mystack.pop();
mystack.push(s[i]);
if(book[s[i]]==mystack.top())

3、几个边界问题
如果输入字符串奇数，false
左括号直接入栈，如果有右括号，没有左括号，false
如果右括号与栈顶不匹配，false
循环完成后，栈内不为空，false

2、力扣22括号生成

递归写法，简洁但是不好理解。回溯，判断回溯很简单，拿到一个问题，你感觉如果不穷举一下就没法知道答案，那就可以开始回溯了。
回溯法的代码套路是使用两个变量： res 和 path，res 表示最终的结果，path 保存已经走过的路径。如果搜到一个状态满足题目要求，就把 path 放到 res 中。
但是这个代码不是很懂？？

class Solution {
     
public:
    vector<string> generateParenthesis(int n) {
     
        vector<string> res;
        int lc = 0, rc = 0;
        dfs(res, "", n, lc, rc);
        return res;
    }
    void dfs(vector<string>& res, string path, int n, int lc, int rc) {
     
        if (rc > lc || lc > n || rc > n) return;
        if (lc == rc && lc == n) {
     
            res.push_back(path);
            return;
        }
        dfs(res, path + '(', n, lc + 1, rc);
        dfs(res, path + ')', n, lc, rc + 1);
    }
};

关于回溯法，weiwei大神在46题有讲解，自己做一下记录。
回溯法，就是树形结构的深度优先遍历，而深度优先遍历在回到上一层结点时需要状态重置。

3、力扣921使括号有效的最少添加

左右括号应该平衡，此时添加为0。定义左右两个变量，从前到后遍历，如果是左括号，就将左变量加一，如果是右括号，如果左变量大于0的情况，说明成功配对，减1，如果左变量为0，说明不平衡，需要添加左括号，右变量加一，最终返回左右变量之和。

三、单调栈

1、力扣84柱状图中最大的矩形

最开始采用暴力解法，遍历每一个矩形面积，找到最大的值，但是有两个测试用例不通过，超出时间限制。。。。

//暴力法
for(int i=0;i<len;i++)
{
     
    int minArea=INT_MAX;
    for(int j=i;j<len;j++)
    {
     
        minArea=min(minArea,heights[j]);
        int area=minArea*(j-i+1);
        ans=max(ans,area);
    }
}  

官方题解，学习单调栈：42,739,496,316,901,402,581
1、单调栈分为单调递增栈和单调递减栈。
（1）栈内的元素是递增的
（2）当元素出栈时，说明这个新元素是出栈元素向后找第一个比其小的元素
（3）当元素出栈后，说明新栈顶元素是出栈元素向前找第一个比其小的元素
2、操作规则（下面都以单调递增栈为例）
（1）如果新的元素比栈顶元素大，就入栈
（2） 如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

单调栈写法模板

stack<int> st;
for(int i = 0; i < nums.size(); i++)
{
     
	while(!st.empty() && st.top() > nums[i])
	{
     
		st.pop();
	}
	st.push(nums[i]);
}

做题思路：对于一个高度，如果能得到向左和向右的边界，那么就能对每个高度求一次面积；遍历所有高度，即可得出最大面积，使用单调栈，在出栈操作时得到前后边界并计算面积；找到最高的那个，两侧严格小于。后进先出，想到栈，什么时候出栈，当前元素严格小于栈顶元素，就能计算出栈顶元素能画出的最大矩形的面积。
代码学习

class Solution {
     
public:
    int largestRectangleArea(vector<int>& heights) {
     
    int ans = 0;
    vector<int> st;
    heights.insert(heights.begin(), 0);  //头部插入0
    heights.push_back(0);   //尾部插入0
    for (int i = 0; i < heights.size(); i++)
    {
     
        while (!st.empty() && heights[st.back()] > heights[i])
        {
     
            int cur = st.back();
            st.pop_back();
            int left = st.back() + 1;
            int right = i - 1;
            ans = max(ans, (right - left + 1) * heights[cur]);
        }
        st.push_back(i);   //压入的是索引
    }
    return ans;
    }
};

四、第K大

1、力扣215数组第k大

要求找到数组中第k个最大的元素，首先想到的是暴力法，先把数组排序，想想下标索引规律，用长度减去k。就是想要的答案。
但是不对，用分治思想，快排中的partition，每次操作，总能排定一个元素，还能够知道这个元素最后的位置。输入当前数组，和左右边界，运用快速排序，得到当前快排索引，然后去和题目要求的索引作比较就可以。贴上partition的代码，注意刚开始的时候，要用随机数。

int partition(vector<int> piles,int left,int right)
{
     
    srand((unsigned)time(NULL));
    swap(piles[left],piles[rand()%(right-left+1)+left]);

    int temp=piles[left];
    while(left<right)
    {
     
        while(left<right && piles[right]>=temp)
            right--;
        piles[left]=piles[right];
        while(left<right && piles[left]<temp)
            left++;
        piles[right]=piles[left];
    }
    piles[left]=temp;
    return left;
}

主函数中的调用：

int findKthLargest(vector<int>& nums, int k) {
     
int len=nums.size();
int target=len-k;

int left=0,right=len-1;
while(true)
{
     
    int pos=parti(nums,left,right);
    if(pos==target)
        return nums[pos];
    else if(target<pos)
        right=pos-1;
    else
        left=pos+1;
}
}

2、力扣230二叉树中第k小

这个题，先知道二叉树的写法

struct TreeNode {
     
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode() : val(0), left(nullptr), right(nullptr) {
     }
     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {
     }
     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {
     }
 };

以及树的遍历方法，DFS的3种遍历，还有BFS。

递归写法？？简洁但是难懂啊??

class Solution {
     
    int n=0;
    int res=0;

public:
void  dfs(TreeNode* root,int k)
{
     
        if(!root)return ;
        dfs(root->left,k);
        n++;
        if(n==k) res=root->val;
        dfs(root->right,k);
  }


public:
    int kthSmallest(TreeNode* root, int k)
     {
          
        dfs(root,k);
        return res;      
    }
};

3、力扣378有序矩阵的第k小

这个和第一个类二维数组中的搜索有点像，矩阵行列都是升序排列。
(1)首先想到的是，把这个二维数组直接变成一维升序排列的数组，然后直接查询就可以。
(2)但是对于有规律排序的二维数组，还是可以想到二分查找。怎么划分查找边界，是个问题。可以统计矩阵中小于等于mid值num总共有多少个，如果比k大，那么当前值是大于k的，如果少，那么小于k，用二分判断，第k小。。
对二分查找的理解还不是很到位，什么时候取，结果可能存在的区域。把包含目标元素划分到小于等于的区域，如果check函数返回true，要缩小右侧，且包含目标元素，如果返回false，说明是严格小于目标值，left=mid+1。

4、力扣703数据流中第k大

用到priority_queue，优先队列Type为数据类型， Container为保存数据的容器，Functional为元素比较方式。如果不写后两个参数，那么容器默认用的是vector，比较方式默认用operator<，也就是优先队列是大顶堆，队头元素最大。

//升序队列
priority_queue < int,vector< int >,greater< int > > q;
//降序队列
priority_queue <int,vector< int >,less< int > > q;

用好优先队列，事半功倍，太巧妙了。。首先第一个成员函数读取k，以及原始数组，采用升序排列的优先队列，需要pop小顶堆，队列里只存k个数，一旦长度大于k。就把头部弹出，那么最终输出的的top就是当前数据流第k大的数据。调用add函数增加数组元素，和之前操作一样，只保留三位数，最终返回的是top。
学到优先队列，贴上这个类的写法。

class kthLargest{
     
    int global_k;
    priority_queue<int ,vector<int>,greater<int> >  pp;
    public:
        kthLargest(int k,vector<int>& nums){
     
        for(int n:nums)
        {
     
            pp.push(n);
            if(pp.size()>k)
                pp.pop();
        }
        global_k=k;
            
        }
    public:
        int add(int val)
        {
     
            pp.push(val);
            if(pp.size()>global_k)
                pp.pop();
            return pp.top();
        }
};

五、cache

1、力扣146 LRU

有两点：(1)最近使用的放在最前面；
(2)如果key重复则更新其对应的val，同时将键值对提前到开头。
要让 put 和 get 方法的时间复杂度为 O(1)，我们可以总结出 cache 这个数据结构必要的条件：查找快，插入快，删除快，有顺序之分。因为显然 cache 必须有顺序之分，以区分最近使用的和久未使用的数据；而且我们要在 cache 中查找键是否已存在；如果容量满了要删除最后一个数据；每次访问还要把数据插入到队头。所以采用哈希链表，双向链表和哈希表的结合体。哈希查找快，双向链表，头部添加节点快，删除快。
先理清楚逻辑关系，贴一段伪代码

// key 映射到 Node(key, val)
HashMap<Integer, Node> map;
// Node(k1, v1) <-> Node(k2, v2)...
DoubleList cache;

int get(int key) {
     
    if (key 不存在) {
     
        return -1;
    } else {
             
        将数据 (key, val) 提到开头；
        return val;
    }
}

void put(int key, int val) {
     
    Node x = new Node(key, val);
    if (key 已存在) {
     
        把旧的数据删除；
        将新节点 x 插入到开头；
    } else {
     
        if (cache 已满) {
     
            删除链表的最后一个数据腾位置；
            删除 map 中映射到该数据的键；
        } 
        将新节点 x 插入到开头；
        map 中新建 key 对新节点 x 的映射；
    }
}

自己实现，双向链表和哈希表。。。

struct DLinkedNode {
     
    int key, value;
    DLinkedNode* prev;
    DLinkedNode* next;
    DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {
     }
    DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {
     }
};

unordered_map<int, DLinkedNode*> cache;  //哈希链表

理清楚逻辑思路。。。
多看几次。思路清晰怎么写，慢慢积累。

2、力扣460 LFU

set底层实现是平衡搜索二叉树。
双散列表方法，时间空间复杂度都是O(1)。

六、二叉树

1、力扣105重建二叉树

首先明确，不管是前序遍历还是中序遍历，结点个数都是一样的，明确递归边界条件。先遍历一遍中序，建立对应的哈希映射，方便后面查找根节点在中序遍历中的位置。递归就是要从规律中找到递归条件，从根节点开始建立这颗二叉树。
注意中括号和小括号，哈希表建立，前后边界。
unordered_map index;

七、动态规划

1、力扣64最小路径和

这个题目是一个简单地动态规划经典案例。对于最小路径和问题来说，二维数组里，只能向右或是向下走，那么，第一行，第一列，只有一个方向没有选择余地，其它地方，取向下或者是向右的最小代价，然后加上当前值，代价和最小的路径返回，也就是dp数组的右下角的最后一个值。
建立一个和原数组相同大小的二维矩阵，存储当前最小的代价和。

2、力扣120三角形最小路径和

这个和上一题基本相同，但是开空间的时候，有优化的空间不必n*n。
状态转移有两个特殊条件，一个是下一行的第一列，只能从上一行来，二是最后一列只能从上一行最后一列来，而且三角形遍历的时候，j 从状态转移方程可以看出，dp只与前一行有关，所以可以只用两行来交替存储，类似于滚动数组，利用对2求余的方法来决定写入哪一行，注意最终返回的是正确的哪一行。

八、链表

1、力扣206反转链表

这道题可以用双指针来解决，先在纸上画出来链表翻转的顺序。首先申请两个指针cur和pre，pre在前，分四步对当前节点进行反转。一是先申请一个临时指针temp用于存放pre的下一个结点，二是把pre的下一节点指向cur，三是把cur向前移动等于pre，四是把pre向前移动到temp，一直运行到链表等于null。

2、力扣92反转链表II

怎么递归的翻转一个单链表？？
反转整个单链表

ListNode reverse(ListNode head) {
     
    if (head.next == null) return head;
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

递归要有base case，就是只有一个节点的时候，直接返回自己。
当链表递归反转之后，新的头结点是 last，而之前的 head 变成了最后一个节点，别忘了链表的末尾要指向 null。
反转前n个结点

ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
     
    if (n == 1) {
      
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);

    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}    

具体的区别：

1、base case 变为 n == 1，反转一个元素，就是它本身，同时要记录后驱节点。

2、刚才我们直接把 head.next 设置为 null，因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了，所以要记录后驱 successor（第 n + 1 个节点），反转之后将 head 连接上。
反转中间的一部分
先看是不是从头开始，即m==1？

ListNode reverseBetween(ListNode head, int m, int n) {
     
    // base case
    if (m == 1) {
     
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

运用之前双指针的思想也可以理解，就是在m到n之间，调换顺序。现申请dummy和pre，还有一个cur，换顺序的时候，还有一个临时结点temp，最终返回dummy->next。

3、力扣21合并两个有序链表

这道题属于简单题。采用迭代法。声明两个指针，第一个指针用于维护返回的头指针，第二个用于指向下一步应该获取的链表结点。循环终止条件是两个链表都不为空，如果1<2，那么指针2指向1，同时1移到下一位，反之，指针2指向2，同时2指向下一个结点。注意：这里指针2是在一个if-else选择结构里面，也就是只能执行一次，所以在这两个选择结构之外让指针2指向下一个结点。最后需要判断，哪一个链表没有完，由于是有序链表，直接指向就可以了。

4、力扣23合并k个升序链表（tencent）

这道题是上一题的延伸。
首先也是要考虑两个链表怎么合并？多一步边界考虑，if ((!a) || (!b)) return a ? a : b;
1 、可以用最简单也是最容易想到的方法，两两合并，利用之前写的两个链表合并的子函数，使链表数组里的链表两两合并，但是要注意，链表的虚拟头，最好直接用链表数组的第一个，因为val是-1或者是0也会参与运算。
2、用优先队列，会自动排序。建立一个小顶堆，也就是降序排列的优先队列。让链表数组中每个链表的头入队，弹出该元素之后，该链表后移，直到为空。可以这样做的原因是链表数组都是有序的。优先队列的比较函数，需要重新定义比较规则。
第一种写法：

struct comp
{
     
    bool operator()(ListNode* l1,ListNode* l2){
     
        return l1->val >l2->val;
    }
};

priority_queue<ListNode*,vector<ListNode*>,comp >  pp;  //小顶堆

第二种写法：

 struct Status {
     
        int val;
        ListNode *ptr;
        bool operator < (const Status &rhs) const {
     
            return val > rhs.val;
        }
    };

还有之前多米诺骨牌的，也是这样用的

关于运算符重载，需要再看看？？

关于优先队列的逻辑，仔细看看，怎么弹出，怎么读取

while(!pp.empty())
        {
     
            ListNode* top=pp.top();
            pp.pop();
            dummy->next=top;
            dummy=top;
            if(top->next)
            pp.push(top->next);
        }

九、回文

1、力扣5最长回文子串

经典的动态规划问题，就是用空间换时间，但是要注意，动态规划的无后效性，注意填表顺序，由于参考的是左下角的数值，所以要先计算出来。第一步申请一个字符串长度n的n*n二维数组，由于l<=r的，所以只需要填写上半部分。对角线上是单个字符，肯定属于回文，如果连续两个字符相等，也是属于回文，这样可以直接给dp数组赋值，在j-i>=3的情况下，开始遍历。

for(int l=3;l<=len;l++)
        {
     
            for(int i=0;i+l-1<len;i++)
            {
     
                int j=i+l-1;
                if(dp[i+1][j-1] ==1 && s[i] == s[j])
                {
     
                    dp[i][j]=1;
                    max=l;
                    start=i;
                }
            }
        }

2、力扣516最长回文子序列

十、位运算

1、力扣136只出现一次的数字

这个真是没想到。。可以使用哈希表，存储数组中每个数字出现的次数，但是需要O(n)的额外空间。用异或。。

很简洁，且好懂，记住！

2、力扣137 II

这个题目的通用解法，如果一个数组里，其它数出现了k次，一个数出现了一次。分情况讨论，如果k是偶数，那么也直接用异或的方法，反之如果k是奇数，就在为1的位对k求余，出现k次，求余为0，1次的话求余为1。写法？？计算机存储32位？

for (int i = 0; i < 32; ++i) {
     
int cnt = 0;
for (auto x : nums) {
     
    cnt += (x>>i)&1;
}
res |= (cnt%3)<<i;
}

这个方法太巧妙了。统计二进制每一位上1的个数。比如2 2 3 2，最初i=0，就是统计最后一位1的个数，1的二进制是0001，所以&之后+=为1，因为只有3的末尾为1，res=1；第二次循环，i=1，四个数右移1位，就是统计倒数第二位上1 的个数，四个都有，求余就是1，再左移一位，就是2，res进行|=，即0010和0001的或等，就是最终结果3。后续计算都是徒劳的，因为所有的位都是0了。

3、力扣260 III

用到一个知识：unordered_set和unordered_map
unordered_set可以把它想象成一个集合，它提供了几个函数让我们可以增删查：

unordered_set::insert
unordered_set::find
unordered_set::erase

unorder版本的map和set只提供前向迭代器（非unorder版本提供双向迭代器）。集合重复插入相同的值是没有效果的。find的返回值是一个迭代器(iterator)，如果找到了会返回指向目标元素的迭代器，没找到会返回end()。
unordered_map存的是键值对key/value，用于索引，插入和查找写法如下：我们这里要插入的是一个key/value pair(键值对)，所以要用make_pair函数把一个字符串和一个整数打包成一个pair。可以用first和second去拿到对应的key和value。

 unordered_map<string,int> mymap;
 mymap.insert(make_pair("c++",100));
 //m_map.insert(map::value_type("hello",5)）;
 auto itr=mymap.find("c++");
 cout<< itr->first<<itr->second<<endl;

需要注意：插入insert返回的是迭代器。如果我们用pair< map::iterator,bool> > rent来接收，则rent->second即是成功与否的标志；rent->first就是返回的map::iterator迭代器；rent->first.first就是string类型的数据。
find返回的也是一个迭代器，iterator。完整写法unordered_map::iterator。如果find没找到，这样写if(mymap.find("java")==mymap.end())。
unordered_map重载了[]运算符，我们可以把key放在中括号里，像操作数组一样操作unordered_map：

mymap["java"]=200;
mymap["java"]++;   //cout结果是201

第一种方法：用unordered_set集合数不重复的特点

 unordered_set<int> myset;
 for(int num:nums)
 {
     
     if(!myset.insert(num).second)
     myset.erase(num);
 }
 vector<int> res(myset.begin(),myset.end());

第二种方法：位运算
这种方法太巧妙了。灵活运用位运算，因为数组里，有两个数是只出现了一次，所以把所有数字都按位异或，就能得到这两个数按位异或的和值，那么，怎么区分开这两个数呢。这是两个不同的数，所以在二进制表达上肯定会有不同，任意一个值为1的比特位便表示了两个数的不同。要让其他位置零，就取反再按位求与，但是这样所有都为0了。所以取反加1再求与，就能反应这两个数字的不同，这也是计算机中求一个数的负数的做法，注意运算优先级的结合关系，不确定就加括号。if((res & nums[i] )== res),记得要给变量初始化啊啊啊啊啊，如果函数返回vector，这两种写法都可以

vector<int> ans;
ans.push_back(n1);
ans.push_back(n2);
/
return {
     n1,n2};

十一、岛屿问题&二维数组

1、力扣200岛屿数量

有两种解决方法，DFS和BFS。二维矩阵，可以看作邻接矩阵，只有上下或者是左右之间才有边。
方法1：DFS（前序遍历）
递归写法？？如果有一个点是1，要先把遍历过的置为0，然后深度遍历（递归）前后左右的点。有一点需要注意，先判断边界条件，如果输入的行为0，即输入一个空数组，就返回0。这一步需要在列赋值之前写。

class Solution {
     
public:
void dfs(vector<vector<char>>& grid,int i,int j)
{
     
    int nr=grid.size();
    int nc=grid[0].size();
    
    grid[i][j]='0';
    if(i-1>=0 && grid[i-1][j]=='1')  dfs(grid,i-1,j);
    if(i+1<nr && grid[i+1][j]=='1')  dfs(grid,i+1,j);
    if(j-1>=0 && grid[i][j-1]=='1')  dfs(grid,i,j-1);
    if(j+1<nc && grid[i][j+1]=='1')  dfs(grid,i,j+1);

}

    int numIslands(vector<vector<char>>& grid) {
     
        int rows=grid.size();
        //int cols=grid[0].size();
        if(rows==0) return 0;
        int cols=grid[0].size();
        int nums=0;

        for(int i=0;i<rows;++i)
        {
     
            for(int j=0;j<cols;++j)
            {
     
                if(grid[i][j]=='1')
                {
     
                    nums++;
                    dfs(grid,i,j);
                }
            }
        }
        return nums;
    }
};

方法2：BFS（层序遍历）
如果队列是两个数，要用pair。queue> neighbors;这样要注意取的是那个，first还是second！！！！在队列里要用这两个元素。
广度优先遍历的要点在于，队列，从一个点开始，层层遍历和他相接的结点，最开始要获取队首，弹出队首，压入与弹出元素相接的元素。循环直到队列为空。

class Solution {
     
public:
    int numIslands(vector<vector<char>>& grid) {
     
        int rows=grid.size();
        if(rows==0) return 0;
        int cols=grid[0].size();
        int nums=0;

        for(int i=0;i<rows;++i)
        {
     
            for(int j=0;j<cols;++j)
            {
     
                if(grid[i][j]=='1')
                {
     
                    nums++;
                    grid[i][j]='0';
                    queue<pair<int,int> >  neighbors;
                    neighbors.push({
     i,j});
                    while(!neighbors.empty())
                    {
     
                        auto elem=neighbors.front();
                        neighbors.pop();
                        int row=elem.first,col=elem.second;
                        if(row-1>=0 && grid[row-1][col]=='1')
                        {
     
                            neighbors.push({
     row-1,col});
                            grid[row-1][col]='0';
                        }
                        if(row+1<rows && grid[row+1][col]=='1')
                        {
     
                            neighbors.push({
     row+1,col});
                            grid[row+1][col]='0';
                        }
                        if(col-1>=0 && grid[row][col-1]=='1')
                        {
     
                            neighbors.push({
     row,col-1});
                            grid[row][col-1]='0';
                        }
                        if(col+1<cols && grid[row][col+1]=='1')
                        {
     
                            neighbors.push({
     row,col+1});
                            grid[row][col+1]='0';
                        }
                    }
                }
            }
        }

        return nums;
    }
};

2、力扣1254

这个题和前面那个很像，注意细节。
统计封闭岛屿的数量，只要有一个边是通的，就返回0；

for(int index=0;index<4;++index)
{
     
     int next_i=i+di[index],next_j=j+dj[index];
     res=min(res,dfs(grid,next_i,next_j));
}

3、力扣695

一样的套路。
统计面积，每遍历一个，就加一个结果值。
记得把遍历过的地方重新置0或者置1。

for(int index=0;index<4;++index)
{
     
    int next_i=i+di[index],next_j=j+dj[index];
    res+=dfs(grid,next_i,next_j);
}

4、力扣135分糖果（附加题）

前后扫描一遍。
首先确保每个孩子都有一颗糖，前向遍历，后面一个评分高于前一个的话，糖数组加一，后向遍历，前一个分数高于后一个，并且前一个糖少于后一个糖加1，这时候就给前面的那个加糖，最终求糖数组的和。

十二、简单二叉树BFS

1、力扣102

我们可以用一种巧妙的方法修改 BFS：
首先根元素入队
当队列不为空的时候
求当前队列的长度 si，依次从队列中取 si个元素进行拓展，然后进入下一次迭代
vector 中begin(),end()返回收首尾元素的值，front(),back()返回首尾元素的引用。
写BFS的思路：申请一个队列，存放树的指针，先 push根节点，还需要一个存放结果的二重vector，如果队列非空，定义当前队列size，如果size–非空，先取出队列的头部，弹出，在vector中存val，队列中push当前左节点，右节点，最后把vector中的数push。
也就是，BFS使用队列，把每个还没有搜索到的点依次放进队列，然后弹出队列的头部元素当做当前遍历点。

2、力扣103

就是需要知道当前遍历到第几层。
简单使用对2求余，不能通过所有案例。

3、力扣104

使用深度优先遍历，就是左子树和右子树的最大值，加一就好。

4、力扣199

十三、Heap第k小的对

1、力扣373

在遇到这种求前k个最大（最小）的问题时候，很自然的想到使用堆来减少时间复杂度，使用优先队列。题目有点难度。参考其中一个答案。

priority_queue <pair<int,pair<int,int> >,vector<pair<int, pair<int, int> > >, cmp > q;

这里主要是pair >，第一个int表示num1中的数值，内层pair分别存储nums2的数值和下标。
1、初始化

for (int i = 0; i < len1; i++) {
     
    pair<int, pair<int, int> > t(nums1[i], pair<int, int>(nums2[0] , 0));
    q.push(t);
}

2、迭代

目前最小的是(i, j) 这一对，那么下一个最小的有可能是(i+1, j)和(i, j+1)。

2、力扣1439

3、力扣719

4、剑指offer49 丑数（附加题）

十四、双指针

1、力扣424

这道题，和字节跳动的完美字符串其实是一样的。遍历26个字母，看是哪个字母在重复，写起来比较简单。双指针，每次发现一个不同的字符，就将used变量加1，如果超过可以使用的次数，就向右移动左指针，一直到第一个不同字符，然后重新开始统计。

2、力扣713乘积小于K的子数组

使用双指针解决该问题。先用一个变量来计数nums，移动右指针，每向数组中增加一个数，而且不超过k，就将计数器加，例如{10}，nums=1，{10,5}，nums=1+2，{10,5,2}，nums=3+3.涉及到怎么计算连续子数组的个数，right-left+1。当超过k时，右移左指针，直到小于k，但同时也需要将总和除以左指针右移对应的那个数值。
需要注意的是，边界条件的判断，还有左指针右移的条件，是乘积超出了限定值而且左指针小于等于右指针。

3、力扣1004

基本和完美字符串套路一样，写法也差不多。使用双指针。

4、剑指48最长不含重复字符的子字符串（附加）

这个题目包含动态规划的思想。首先要建一个26维的数组，用于保存某一个字母在数组中上一次出现的位置，初值赋为-1，表示还从没有出现过。然后是算法部分，用f(i)表示以第i个字符结尾的不包含重复字符的字符串的最大长度。如果第i个字符没有出现过，那么就直接等于f(i-1)+1，如果出现过，就要分两种情况讨论。一个是距离d<=f(i-1)，f(i)=d；一个是d>f(i-1)，因为已经很远了，所以f(i)=f(i-1)+1。
不知道为什么不能通过所有案例？？？

5、力扣3无重复字符的最长子串

如果我们依次递增地枚举子串的起始位置，那么子串的结束位置也是递增的！这里的原因在于，假设我们选择字符串中的第 kk 个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为rk。那么当我们选择第 k+1个字符作为起始位置时，首先从 k+1到 rk的字符显然是不重复的，并且由于少了原本的第 k个字符，我们可以尝试继续增大 rk，直到右侧出现了重复字符为止。
需要使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合
右指针-1开始，左指针0开始。如果左指针开始移动了，就要删掉集合里之前的数，如果右指针移动，而且这个数字还没有开始出现过，就加入集合。返回最大值。

十五、二叉树的遍历

1、力扣144前序

用一个套路写树的遍历。

class Solution {
     
public:
    vector<int> preorderTraversal(TreeNode* root) {
     
        vector<int> res;  //保存结果
        stack<TreeNode*> call;  //调用栈
        if(root!=nullptr) call.push(root);  //首先介入root节点
        while(!call.empty()){
     
            TreeNode *t = call.top();
            call.pop();  //访问过的节点弹出
            if(t!=nullptr){
     
                if(t->right) call.push(t->right);  //右节点先压栈，最后处理
                if(t->left) call.push(t->left);
                call.push(t);  //当前节点重新压栈（留着以后处理），因为先序遍历所以最后压栈
                call.push(nullptr);  //在当前节点之前加入一个空节点表示已经访问过了
            }else{
       //空节点表示之前已经访问过了，现在需要处理除了递归之外的内容
                res.push_back(call.top()->val);  //call.top()是nullptr之前压栈的一个节点，也就是上面call.push(t)中的那个t
                call.pop();  //处理完了，第二次弹出节点（彻底从栈中移除）
            }
        }
        return res;
    }
};

递归写法

class Solution {
     
public:
    vector<int> ans;
    void preorder(TreeNode* root){
     
        if(root == NULL) return;
        ans.push_back(root->val);
        preorder(root->left);
        preorder(root->right);
    }
    vector<int> preorderTraversal(TreeNode* root) {
     
        preorder(root);
        return ans;
    }
};

2、力扣94中序

class Solution {
     
public:
    vector<int> inorderTraversal(TreeNode* root) {
     
        vector<int> res;
        stack<TreeNode*> call;
        if(root!=nullptr) call.push(root);
        while(!call.empty()){
     
            TreeNode *t = call.top();
            call.pop();
            if(t!=nullptr){
     
                if(t->right) call.push(t->right);
                call.push(t);  //在左节点之前重新插入该节点，以便在左节点之后处理（访问值）
                call.push(nullptr); //nullptr跟随t插入，标识已经访问过，还没有被处理
                if(t->left) call.push(t->left);
            }else{
     
                res.push_back(call.top()->val);
                call.pop();
            }
        }
        return res;
    }
};

class Solution {
     
public:
    vector<int> ans;
    void inorder(TreeNode* root){
     
        if(root == NULL) return;
        inorder(root->left);
        ans.push_back(root->val);
        inorder(root->right);
    }
    vector<int> inorderTraversal(TreeNode* root) {
     
       inorder(root);
       return ans; 
    }
};

3、力扣145后序

class Solution {
     
public:
    vector<int> preorderTraversal(TreeNode* root) {
     
        vector<int> res;  //保存结果
        stack<TreeNode*> call;  //调用栈
        if(root!=nullptr) call.push(root);  //首先介入root节点
        while(!call.empty()){
     
            TreeNode *t = call.top();
            call.pop();  //访问过的节点弹出
            if(t!=nullptr){
     
                if(t->right) call.push(t->right);  //右节点先压栈，最后处理
                if(t->left) call.push(t->left);
                call.push(t);  //当前节点重新压栈（留着以后处理），因为先序遍历所以最后压栈
                call.push(nullptr);  //在当前节点之前加入一个空节点表示已经访问过了
            }else{
       //空节点表示之前已经访问过了，现在需要处理除了递归之外的内容
                res.push_back(call.top()->val);  //call.top()是nullptr之前压栈的一个节点，也就是上面call.push(t)中的那个t
                call.pop();  //处理完了，第二次弹出节点（彻底从栈中移除）
            }
        }
        return res;
    }
};

class Solution {
     
public:
    vector<int> ans;
    void postorder(TreeNode* root){
     
        if(root == NULL) return;
        postorder(root->left);
        postorder(root->right);
        ans.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
     
        postorder(root);
        return ans;
    }
};

十六、窗口

1、力扣239滑动窗口

首先知道一个结论：在一堆数字中，已知最值，如果给这堆数添加一个数，那么比较一下就可以很快算出最值；但如果减少一个数，就不一定能很快得到最值了，而要遍历所有数重新找最值。回到这道题的场景，每个窗口前进的时候，要添加一个数同时减少一个数，所以想在 O(1)的时间得出新的最值，就需要「单调队列」这种特殊的数据结构来辅助了。
一个单调队列的操作

class MonotonicQueue {
     
    // 在队尾添加元素 n
    void push(int n);
    // 返回当前队列中的最大值
    int max();
    // 队头元素如果是 n，删除它
    void pop(int n);
}

思路就是先申请一个单调队列，和一个vector，开始的时候，先把当前窗口k-1个数字填满，在窗口移动的时候，先push最后一个数字，将最大值返回到vector，再pop第一个数。
首先我们要认识另一种数据结构：deque，即双端队列。和一般的队列不一样的是，这个队列的push，要把前面比他小的元素都删掉，具体是从后面pop；这样max直接返回front就行了；而如果要pop一个值为n的元素，从前面。

class deque {
     
    // 在队头插入元素 n
    void push_front(int n);
    // 在队尾插入元素 n
    void push_back(int n);
    // 在队头删除元素
    void pop_front();
    // 在队尾删除元素
    void pop_back();
    // 返回队头元素
    int front();
    // 返回队尾元素
    int back();
}

单调队列的 push 方法依然在队尾添加元素，但是要把前面比新元素小的元素都删掉：

class MonotonicQueue {
     
private:
    deque<int> data;
public:
    void push(int n) {
     
        while (!data.empty() && data.back() < n) 
            data.pop_back();
        data.push_back(n);
    }
};

如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序。单调队列在添加元素的时候靠删除元素保持队列的单调性，相当于抽取出某个函数中单调递增（或递减）的部分；而优先级队列（二叉堆）相当于自动排序。自己写单调队列的类：

class MonotonicQueue {
     
private:
    deque<int> data;
public:
    void push(int n) {
     
        while (!data.empty() && data.back() < n) 
            data.pop_back();
        data.push_back(n);
    }
    
    int max() {
      return data.front(); }
    
    void pop(int n) {
     
        if (!data.empty() && data.front() == n)
            data.pop_front();
    }
};

2、力扣992K个不同整数的子数组

给一个数组，和一个k。统计含有k个不同整数的子数组。
首先想到双指针发方法，其实也是一种暴力解法，肯定会超时，将双指针与哈希表结合使用。哈希表来存储当前数组中的数字和出现的次数。就是找恰好包含K个不同整数的子数组。
写代码的思路：申请左右指针初始值都为0，申请一个无序map，存数组中的数字和其出现的次数。将数组中的元素依次存到哈希表中，判断，当前哈希表长度是否大于K，如果大于，就要删去左侧的值，直到小于K，在此同时，要右移左指针。删左侧的值，是要先减出现的次数，然后因为一直右移左指针，遇到只出现一次的元素，erase之后窗口长度就小于K了。如果窗口长度正好是K，就说明恰好有两个不同元素，就是计算能组成几个子数组，,每循环一次，ans加1，这里用到临时的一个指针，是用来算次数的，所以用过之后要把哈希表内的数据恢复。

while(window.size()>K)
 {
     
     if(window[A[left]]>1)
     window[A[left]]--;
     else
     window.erase(A[left]);

     left++;
 }
 while(window.size()==K)
 {
     
     ans++;
     if(window[A[temp]]>1)
     window[A[temp]]--;
     else
     window.erase(A[temp]);

     temp++;
 }
 while(temp>left)
 {
     
     window[A[temp-1]]++;
     temp--;
 }

3、力扣1358三种字符的子字符串数目

要求特定字符都至少出现一次的子字符串。

十七、并查集

1、力扣200岛屿数量

这道题之前做过，再次回顾。。
深度优先搜索，广度优先搜索，并查集
记得要把遍历过的点置零。上下左右遍历的边界，向上向左是大于等于0，向右向下小于等于行列数。

class Solution {
     
private:
    void dfs(vector<vector<char>>& grid, int r, int c) {
     
        int nr = grid.size();
        int nc = grid[0].size();

        grid[r][c] = '0';
        if (r - 1 >= 0 && grid[r-1][c] == '1') dfs(grid, r - 1, c);
        if (r + 1 < nr && grid[r+1][c] == '1') dfs(grid, r + 1, c);
        if (c - 1 >= 0 && grid[r][c-1] == '1') dfs(grid, r, c - 1);
        if (c + 1 < nc && grid[r][c+1] == '1') dfs(grid, r, c + 1);
    }

public:
    int numIslands(vector<vector<char>>& grid) {
     
        int nr = grid.size();
        if (!nr) return 0;
        int nc = grid[0].size();

        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
     
            for (int c = 0; c < nc; ++c) {
     
                if (grid[r][c] == '1') {
     
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }

        return num_islands;
    }
};

广度优先搜索用到队列，由于需要存储行列，所以需要pair。一直遍历，直到当前队列为空。

class Solution {
     
public:
    int numIslands(vector<vector<char>>& grid) {
     
        int nr = grid.size();
        if (!nr) return 0;
        int nc = grid[0].size();

        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
     
            for (int c = 0; c < nc; ++c) {
     
                if (grid[r][c] == '1') {
     
                    ++num_islands;
                    grid[r][c] = '0';
                    queue<pair<int, int>> neighbors;
                    neighbors.push({
     r, c});
                    while (!neighbors.empty()) {
     
                        auto rc = neighbors.front();
                        neighbors.pop();
                        int row = rc.first, col = rc.second;
                        if (row - 1 >= 0 && grid[row-1][col] == '1') {
     
                            neighbors.push({
     row-1, col});
                            grid[row-1][col] = '0';
                        }
                        if (row + 1 < nr && grid[row+1][col] == '1') {
     
                            neighbors.push({
     row+1, col});
                            grid[row+1][col] = '0';
                        }
                        if (col - 1 >= 0 && grid[row][col-1] == '1') {
     
                            neighbors.push({
     row, col-1});
                            grid[row][col-1] = '0';
                        }
                        if (col + 1 < nc && grid[row][col+1] == '1') {
     
                            neighbors.push({
     row, col+1});
                            grid[row][col+1] = '0';
                        }
                    }
                }
            }
        }

        return num_islands;
    }
};

2、力扣952力扣547或684

联通？？用到求素数的算法

怎么求20以内素数的一个小案例

int main(){
     
    int cnt=0;//用来计数
    
    bool isprime[21];
    for(int i=0;i<=20;i++)isprime[i]=true;//先全部置为真
 
    isprime[0]=isprime[1]=false;//1 0 不是素数
 
    for(int i=2;i<=20;i++){
     //从2开始往后筛
        if(isprime[i]){
     
            for(int j=2*i;j<=20;j+=i){
     
                isprime[j]=false;
            }
        }
        if(isprime[i]){
     
            cnt++;//如果是素数 就计数
        }
    }
    printf("%d",cnt);
}

这道题用埃氏筛法和并查集实现。。。

class Solution {
     
public:
    vector<int> fa, siz;
    int v[100005], ans;
    bool vis[100005];
    int Find(int x){
     
        return (x == fa[x] ? x: (fa[x] = Find(fa[x])));
    }
    void Union(int x, int y){
     
        int fx = Find(x), fy = Find(y);
        if (fx == fy) return ;
        if (siz[fx] > siz[fy]){
     
            fa[fy] = fx, siz[fx] += siz[fy], ans = max(ans, siz[fx]);
        }else {
     
            fa[fx] = fy, siz[fy] += siz[fx], ans = max(ans, siz[fy]);
        }
    }
    int largestComponentSize(vector<int>& A) {
     
        int n = A.size(), maxi = -1;
        memset(v, -1, sizeof(v));
        memset(vis, 0, sizeof(vis));
        fa = vector<int>(n, 0);
        siz = vector<int>(n, 1);
        ans = 0;
        for (int i = 0; i < n; ++i)
            fa[i] = i, v[A[i]] = i, maxi = max(maxi, A[i]);
        for (int i = 2; i <= maxi; ++i){
     
            if (!vis[i]){
     
                int t = -1;
                if (v[i] >= 0) t = v[i];
                for (int j = i + i; j <= maxi; j += i){
     
                    if (v[j] >= 0) {
     
                        if (t < 0) t = v[j];
                        else Union(t, v[j]);
                    }
                    vis[j] = true;
                }
            }
        }
        return ans;
    }
};

3、力扣79（附加题）

回溯法。就是先找到第一个索引，之后上下左右四个方向遍历，递归写。
注意要把遍历过的地方置零。
回溯思想：

private:
    bool backtrack(vector<vector<char>>& board, string& word, int wordIndex, int x, int y){
     
        if( board[x][y] != word[wordIndex]){
      // 当前位的字母不相等，此路不通
            return false;
        }
        if(word.size() - 1  == wordIndex){
      // 最后一个字母也相等, 返回成功
            return true;
        }
        char tmp = board[x][y]; 
        board[x][y] = 0; // 避免该位重复使用
        wordIndex++;
        if((x > 0 && backtrack(board, word, wordIndex, x - 1, y)) // 往上走 
        || (y > 0 && backtrack(board, word, wordIndex, x, y - 1)) // 往左走
        || (x < board.size() - 1 && backtrack(board, word, wordIndex, x + 1, y)) // 往下走
        || (y < board[0].size() - 1 && backtrack(board, word, wordIndex, x, y + 1))){
      // 往右走
            return  true; // 其中一条能走通，就算成功
        }
        board[x][y] = tmp; // 如果都不通，则回溯上一状态
        return false;
    }

十八、链表相关

1、力扣237删除结点

我们看不到链表的head，只知道要删除的结点。直接替换啊。
node的值val等于下一个的val，next等于下一个的next。

2、力扣203移除链表元素

移除确定val的结点，如果在链表中，很轻松。但是如果在链表头，就需要考虑。使用哨兵结点。哨兵节点广泛应用于树和链表中，如伪头、伪尾、标记等，它们是纯功能的，通常不保存任何数据，其主要目的是使链表标准化，如使链表永不为空、永不无头、简化插入和删除。
设置pre和cur结点，还有要删除的结点，维护最终要返回的结点，返回他的下一个结点。
专门用来存储要删除节点的，最后要删除。

if (toDelete != nullptr) {
     
        delete toDelete;
        toDelete = nullptr;
      }

3、力扣19删除倒数第N

典型的双指针，快慢指针，快的先N步出发。
先申请要返回的结果结点，当快指针结束的时候，慢指针刚好到要删除的地方。

4、力扣141链表环

判断链表中是否有环。
数组和链表：数组，所有元素都连续的存储于一段内存中，且每个元素占用的内存大小相同。这使得数组具备了通过下标快速访问数据的能力。但连续存储的缺点也很明显，增加容量，增删元素的成本很高，时间复杂度均为 O(n)。增加数组容量需要先申请一块新的内存，然后复制原有的元素。如果需要的话，可能还要删除原先的内存。删除元素时需要移动被删除元素之后的所有元素以保证所有元素是连续的。增加元素时需要移动指定位置及之后的所有元素，然后将新增元素插入到指定位置，如果容量不足的话还需要先进行扩容操作。
一般来讲，链表中只会有一个结点的指针域为空，该结点为尾结点，其他结点的指针域都会存储一个结点的内存地址。链表中也只会有一个结点的内存地址没有存储在其他结点的指针域，该结点称为头结点。
快慢指针的特性 —— 每轮移动之后两者的距离会加一。用快慢指针解决这个问题，如果有环，总会追上的。

5、力扣142环的入口

要找环的入口。依然是设置快慢指针。有一个数学推理，起点，入口，相遇点之间的关系。快指针一次走两步，慢指针一次走一步。找到相遇点后定义两个指针分别指向起点和相遇点，然后一起走，再次相遇就是环的起点。记住吧，不推理了。

while(fast!=NULL&&fast->next!=NULL)
{
     
    slow=slow->next;
    fast=fast->next->next;
    if(slow==fast){
     
        slow=head;
        while(slow!=fast){
     
            slow=slow->next;
            fast=fast->next;
        }
        return fast;
    }
}

6、力扣160相交链表

美团面试过。
双指针，有相交必会相遇啊。
A的指针遍历完A 接着从headB开始遍历
B的指针遍历完B 接着从headA开始遍历
两个指针都最多走m + n。
当两个指针同时为空时，表示不相交；当两个都非空且相等时，表示相交。

 ListNode* cur_a = headA;
 ListNode* cur_b = headB;

  while(cur_a != cur_b)
  {
     
      cur_a = (cur_a ? cur_a->next : headB);
      cur_b = (cur_b ? cur_b->next : headA);
  }

十九、全为1的矩形面积

1、力扣85最大面积

一个特别巧妙的方法，利用动态数组，转化为84题单调栈的解法。
动态数组存每一列1的高度。
很巧妙。

2、力扣221

算正方形，和矩形不同的是，这个面积是直接边长平方。
用动态规划，另开一个数组存储右下角元素的最大边长。

代码很清楚

class Solution {
     
public:
    int maximalSquare(vector<vector<char>>& matrix) {
     
        if (matrix.size() == 0 || matrix[0].size() == 0) {
     
            return 0;
        }
        int maxSide = 0;
        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<int>> dp(rows, vector<int>(columns));
        for (int i = 0; i < rows; i++) {
     
            for (int j = 0; j < columns; j++) {
     
                if (matrix[i][j] == '1') {
     
                    if (i == 0 || j == 0) {
     
                        dp[i][j] = 1;
                    } else {
     
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
};

二十、回溯

1、力扣17电话号码的字母组合

首先想到用map记录，每个数字对应的字母。
采用回溯算法，每次取一个数字，遍历所有可能的组合最终输出所有可能的组合。
注意map的写法，输入的是字符和字符串，单引号和双引号。

void DFS(int index,string digits)
    {
     
        if(index==digits.size())
        {
     
            ans.push_back(current);
            return;
        }

        for(int i=0;i<MM[digits[index]].size();i++)
        {
     
            current.push_back(MM[digits[index]][i]);   //压入
            DFS(index+1,digits);
            current.pop_back();   //回退
        }
    }

2、力扣22括号

回顾N皇后问题，就是不能出现在同一行，同一列，主对角线，副对角线。
主对角线的下标相减值固定，副对角线差值固定。
一样的回溯算法，思考与深度优先遍历之间的关系。
全排列问题入手。【1,2,3】

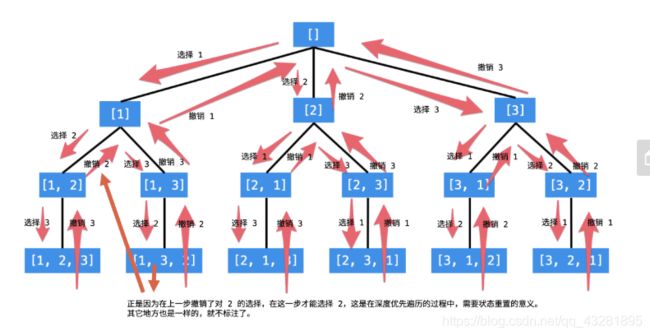
括号生成，回溯法。
存一个path，和一个res。
把符合条件的path都存到结果容器res。

3、力扣39组合总和

数组内的数字可以被重复使用。
寻找所有可行解的题。[2,3,6,7]

以target为根节点，做减法。减到 0或者负数的时候停止，即：结点 00 和负数结点成为叶子结点；所有从根结点到结点 0 的路径（只能从上往下，没有回路）就是题目要找的一个结果。
但是会有重复结果，遇到这一类相同元素不计算顺序的问题，我们在搜索的时候就需要 按某种顺序搜索。具体的做法是：每一次搜索的时候设置 下一轮搜索的起点。

void DFS(int start,int target)
{
     
    if(target == 0)
    {
     
        res.push_back(path);
        return;
    }

    for(int i=start;i<candidates.size() && target-candidates[i]>=0;i++)
    {
     
        path.push_back(candidates[i]);
        DFS(i,target-candidates[i]);
        path.pop_back();
    }
}

下一题，如果数组数据只能用一次呢？？？

void DFS(int start,int target)
{
     
    if(target == 0)
    {
     
        res.push_back(path);
        return;
    }

    for(int i=start;i<candidates.size() && target-candidates[i]>=0;i++)
    {
     
        if(i>start && candidates[i]==candidates[i-1])
        continue;
        path.push_back(candidates[i]);
        DFS(i+1,target-candidates[i]);
        path.pop_back();
    }
}

二十一、股票最佳时机

1、力扣121

股票的一次交易。先买入，再卖出，计算所能获得的最大收益。
数组中两点差，可以转化成求和问题。
最大连续子数组和可以使用动态规划求解， dp[i]表示以 i为结尾的最大连续子数组和，递推公式为：dp[i]=max(0,dp[i−1]+diff[i])。
其实就是要求最低和最高的差。只要大于零就是赚了。
取0和pre+diff中的较大者。
股票问题常用动态规划，因为与前一状态有关。想到动态规划的状态转移方程。
dp[i]=max(dp[i-1],nums[i]-min)，最后一个就是需要的最大收益。

class Solution {
     
public:
    int maxProfit(vector<int>& prices) {
     
        int n = prices.size();
        if (n == 0) return 0; // 边界条件
        int minprice = prices[0];
        vector<int> dp (n, 0);

        for (int i = 1; i < n; i++){
     
            minprice = min(minprice, prices[i]);
            dp[i] = max(dp[i - 1], prices[i] - minprice);
        }
        return dp[n - 1];
    }
};

2、力扣122

第一种方案，贪心算法。逢低买入，逢高卖出。如果[1,2,31000]；按理说第一天买，最后一天卖收益最高，但是一天买一天卖，最后结果是一样的。该算法仅可以用于计算，但计算的过程并不是真正交易的过程，但可以用贪心算法计算题目要求的最大利润。
第二种用动态规划。
一个很神奇的思路，每天都有两种状态，手上有股票或是没有股票。无股票为0，有股票为1。

class Solution {
     
public:
    int maxProfit(vector<int>& prices) {
     
        // 动态规划解法
        
        // 0.初始判断
        if(prices.empty()) return 0;
        
        int dp[prices.size()][2];
        // 1.初始状态
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        // 2.状态转移
        for(int i = 1; i<prices.size();i++){
     
            // 3.状态转移方程
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }
        return dp[prices.size()-1][0];
    }
};

3、力扣123有2笔交易

从简单变困难
不是很懂？？

class Solution {
     
public:
    int maxProfit(vector<int>& prices) {
     
        int n = prices.size();
        if(n == 0) return 0;
        int minPri = prices.front(), maxPro1 = 0; // 顺序遍历的最小pirce和最大利润
        int maxPri = prices.back(), maxPro2 = 0;  // 逆序遍历的最大price和最大利润
        vector<int> profits1(n,0), profits2(n,0); // 顺序和逆序的利润分布
        for(int i = 0; i < n; i++){
     
            if(prices[i] <= minPri) minPri = prices[i];
            else maxPro1 = max(maxPro1, prices[i]-minPri);
            profits1[i] = maxPro1;
            if(prices[n-i-1] >= maxPri) maxPri = prices[n-i-1];
            else maxPro2 = max(maxPro2, maxPri-prices[n-i-1]);
            profits2[n-i-1] = maxPro2;
        }
        int maxPro = profits1[n-1];
        for(int i = 0; i < n-1; i++){
     
            maxPro = max(maxPro, profits1[i]+profits2[i+1]);
        }
        return maxPro;
    }
};

二十二、股票类

1、力扣188有K笔交易

2、力扣309冷冻期

weiwei大神动态规划思路，四步大法
1、交易一次
设置初始状态：dp[i][j]，i指第i天在持股状态为j的情况下获得的最大收益，j指第i天的状态。有两种状态：0和1,0是不持股，特指买入股票又卖出。1指持股。
怎么转移？

// 注意：因为题目限制只能交易一次，因此状态只可能从 1 到 0，不可能从 0 到 1
int[][] dp = new int[len][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < len; i++) {
     
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
}
return dp[len - 1][0];

2、不限制交易次数

dp[0][0] = 0;
dp[0][1] = -prices[0];

for (int i = 1; i < len; i++) {
     
    // 这两行调换顺序也是可以的
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];

3、就两次

public class Solution {
     

    public int maxProfit(int[] prices) {
     
        int len = prices.length;
        if (len < 2) {
     
            return 0;
        }

        // dp[i][j] ，表示 [0, i] 区间里，状态为 j 的最大收益
        // j = 0：什么都不操作
        // j = 1：第 1 次买入一支股票
        // j = 2：第 1 次卖出一支股票
        // j = 3：第 2 次买入一支股票
        // j = 4：第 2 次卖出一支股票

        // 初始化
        int[][] dp = new int[len][5];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        // 3 状态都还没有发生，因此应该赋值为一个不可能的数
        for (int i = 0; i < len; i++) {
     
            dp[i][3] = Integer.MIN_VALUE;
        }

        // 状态转移只有 2 种情况：
        // 情况 1：什么都不做
        // 情况 2：由上一个状态转移过来
        for (int i = 1; i < len; i++) {
     
            // j = 0 的值永远是 0
            dp[i][0] = 0;
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        // 最大值只发生在不持股的时候，因此来源有 3 个：j = 0 ,j = 2, j = 4
        return Math.max(0, Math.max(dp[len - 1][2], dp[len - 1][4]));
    }
}

4、k次不太会

5、冷冻期

int[][] dp = new int[len][3];

// 初始化
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;

for (int i = 1; i < len; i++) {
     
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][2] - prices[i]);
    dp[i][2] = dp[i - 1][0];
}
return Math.max(dp[len - 1][0], dp[len - 1][2]);

3、力扣714

手续费

// dp[i][j] 表示 [0, i] 区间内，到第 i 天（从 0 开始）状态为 j 时的最大收益'
// j = 0 表示不持股，j = 1 表示持股
// 并且规定在买入股票的时候，扣除手续费
int[][] dp = new int[len][2];

dp[0][0] = 0;
dp[0][1] = -prices[0] - fee;

for (int i = 1; i < len; i++) {
     
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
}
return dp[len - 1][0];

二十三、图上的BFS

1、力扣1129

2、力扣1162

3、力扣1306

二十四、拓扑排序

1、力扣207

2、力扣210

3、力扣329

二十五、Trie树

1、力扣208

2、力扣212

3、力扣421

二十六、最短路径

1、力扣743

2、力扣399

二十七、线段树

1、力扣303

2、力扣307

3、力扣315

二十八、DP和sliding window

1、力扣1423

2、力扣322

二十九、

1、力扣1187

2、力扣968

三十、

1、力扣1

2、力扣15

3、力扣18