word2vec模型评估_02. 语言模型（language Model）发展历史

一、导言

本章主要主要介绍语言模型的发展历史，对怎么发展到word2vec进行了简介，对于帮助我们理解word2vec思想或许有些帮助。

非监督式学习得到的词向量（word embedding）已经成功地应用于许多NLP的任务中，它常被誉为是一项利器。实际上，在许多NLP任务中，词向量已经完全地取代了传统的分布特征，比如布朗聚类和LSA特征^[1][2]。

对初学者而言，用词向量来计算词语的语义关系非常容易，NLP方向的深度学习演讲经常把国王 - 男人 + 女人 ≈ 王后的例子作为开篇。在本文中，我们将用词向量（word embeddings）来指代词语在低维向量空间的稠密表征。在英语中，它还可以被称作word vectors或是distributed representations。我们主要关注的是神经网络词向量，即通过神经网络模型学习得到的词向量。

二、词向量的来历

自上世纪90年代开始，特征空间模型就应用于分布式语言理解中。在当时，许多模型用连续型的表征来表示词语，包括潜在语义分析（Latent Semantic Analysis）和潜在狄利克雷分配（Latent Dirichlet Allocation）模型。这个文章中^[3]详细介绍了词向量方法在那个阶段的发展。

Bengio等人在2003年首先提出了词向量的概念，当时是将其与语言模型的参数一并训练得到的。Collobert和Weston在2008年则第一次正式使用预训练的词向量。Collobert和Weston的那篇里程碑式的论文A unified architecture for natural language processing不仅将词向量方法作为处理下游任务的有效工具，而且还引入了神经网络模型结构，为目前许多方法的改进和提升奠定了基础。词向量的真正推广要归因于Mikolov等人于2013年开发的Word2vec，word2vec可以训练和使用词向量。在2014年，Pennington等人发布了GloVe，这是一套预训练得到的完整词向量集，它标志着词向量方法已经成为了NLP领域的主流。

词向量方法是无监督式学习的少数几个成功应用之一。它的优势在于不需要人工标注语料，直接使用未标注的文本训练集作为输入。输出的词向量可以用于下游的业务处理。

三、词向量模型

一般来说，神经网络将词表中的词语作为输入，输出一个低维度的向量表示这个词语，然后用反向传播的方法不断优化参数。输出的低维向量是神经网络第一层的参数，这一层通常也称作Embedding Layer。

生成词向量的神经网络模型分为两种，一种是像word2vec和Glove这样的模型，这类模型的目的就是生成词向量，另一种是将词向量作为副产品产生，两者的区别在于计算量不同。若词表非常庞大，用深层结构的模型训练词向量需要许多计算资源。这也是直到2013年词向量才开始被广泛用于NLP领域的原因。计算复杂度是使用词向量方法需要权衡的一个因素，我们在后面还有讨论。

两种模型的另一个区别在于训练的目标不同：一种是word2vec模型，其目的是训练可以表示语义关系的词向量，它们能被用于后续的任务中；如果后续任务不需要用到语义关系，则按照word2vec方式生成的词向量并没有什么用。另一种模型则根据特定任务需要训练词向量。当然，若特定的任务就是对语言建模，那么两种模型生成的词向量非常相似了。

顺便提一下，word2vec和GloVe在NLP中的地位就相当于VGGNet在机器视觉中的地位，都能够通过简单的训练生成有用的特征。

为了便于比较，我们约定以下符号：假设训练文本集（语料）

（Corpus）含有

个词

，词的数量（# word tokens

^[4]）是

，词典（词表）

的大小是

（# word types），我们只考虑

个词的上下文序列，每个词语对应一个输入词向量

（即Embedding Layer的向量），

维度是

，

输出一个词向量

（另一个词向量）。目标函数用

表示，其中

表示模型的参数，对每个输入值

输出一个得分

。

The term "token" refers to the total number of words in a text, corpus etc, regardless of how often they are repeated. The term "type" refers to the number of distinct words in a text, corpus etc. Thus, the sentence "a good wine is a wine that you like" contains nine tokens, but only seven types, as "a" and "wine" are repeated. A good starting discussion is provided by Mike Scott on the following page ^[4]。

四、语言建模概述

词向量模型与语言模型非常紧密地交织在一起。语言模型的质量评估是基于它们对词语用概率分布的表征能力。事实上，许多最先进的词向量模型都在攻坚的任务就是已有一串词语序列，预测下一个出现的词语将会是什么。词向量模型也常用perplexity的指标进行评测，这项基于交叉熵的指标也是借鉴了语言建模。

在进入词向量模型之前，让我们先来简单地回顾一下基础的语言建模问题。

语言建模的对象是自然语言，即人类文明发展过程中自然演化的语言，不包括编程语言、世界语等。但严格地讲，自然语言也并不完全是自然产生的，而是人为创造出来的。另外，自然语言的表现形式通常分为语音与文字，而语言建模主要针对某种自然语言对应的文字系统，因此将该任务称为“文字系统建模 （Writing System Modeling, WSM）”更为严谨。通常获取某种文字系统下的文本所表达的信息，需要了解对应文字系统的内部结构，以及其与相应自然语言的对应关系。而语言模型仅从文本中构建，能够表示的只有文字系统本身的内部结构信息。虽然采用“文字系统建模”更为严谨，但为了与主流的研究一致，仍然沿用“语言建模”的命名习惯^[5]。

4.1 什么是语言模型呢

语言建模的目的就是构建该自然语言中词序列的分布，然后用于评估某个词序列的概率。如果给定的词序列符合语用习惯，则给出高概率，否则给出低概率。在语言建模过程中，采用了链式法则，单个词序列的概率被分解为序列中各个词的条件概率的乘积，而每个词的条件概率为给定其上文时的该词出现的概率。语言模型因此就是用来计算一个句子的概率的模型(也就是判断一句话是否是人的语言表达方式的概率)。给定一个词汇集合

，对于一个由

中的词构成的序列

，统计语言模型赋予这个序列一个概率

，来衡量

符合自然语言的语法和语义规则的置信度，

就是

语言模型，也称为统计语言模型（Statistical Language Model）。这里的概率指的是组成字符串的这个组合，在训练语料中出现的似然，与句子是否合乎语法无关。假设训练语料来自于人类的语言，那么可以认为这个概率是的是一句话是否是人类语言表达的概率。

首先，由链式法则(chain rule)可以得到

为了保证上述公式的完备性，必须引入一个词

，并且假定

，上述公式满足：

上述语言模型存在两个问题，一是参数空间过大，二是数据稀疏严重。

参数空间过大：假定字符串中字符全部来自与大小为

的词典，上述例子中我们需要计算所有的条件概率，对于所有的条件概率，这里的

都有

种取值，那么实际上这个模型的自由参数数目量级是

，

为字符串的长度。从上面可以看出，模型的自由参数是随着字符串长度的增加而指数级暴增的，这使我们几乎不可能正确的估计出这些参数

^[6]。

数据稀疏性（Data sparsity）：从上面可以看到，每一个

都具有

种取值，这样构造出了非常多的词对，但实际中训练语料是不会出现这么多种组合的，那么依据最大似然估计，最终得到的概率实际是很可能是0，在这种情况下，可能会出现未登陆词(OOV，Out-of-vocabulary)。

4.2 N-gram语言模型

4.2.1 N-gram语言模型定义

针对上面两个问题，我们如何解决，基于马尔科夫假设（Markov Assumption）：下一个词的出现仅依赖于它前面的一个或几个词。基于此假设，定义 n-gram 语言模型如下：

n=1 unigram：

n=2 bigram：

n=3 trigram：

...

n=n n-gram:

在基于n-gram的语言模型中，根据极大似然估计，我们可以基于n-gram出现的频率来计算词语的概率：

针对unigram而言，

其中

是语料库中的总词数（# word tokens）。

例如，我们以bigram模型举例说明，数据集如下所示，

根据bigram模型，

我们有：

利用bigram模型估计句子的概率：

Stanford的这个文档^[7]详细介绍了n-gram模型，大家可以参考，微软的一个长文中详细介绍了n-gram语言模型^[8]。

那么，n-gram 中的参数 n 取多大比较合适呢？一般来说，n 的选取需要同时考虑计算复杂度和模型效果两个因素，这里我们讨论计算复杂度，模型的效果放在4.2.2节讨论。

在计算复杂度方面，上表 给出了 n-gram 模型中模型参数数量随着 m 的逐渐增大而变化的情况，其中假定词典大小

（汉语的词汇量大致是这个量级）。事实上，模型参数的量级是

的指数函数(

，显然 n 不能取得太大，实际应用中最多的是采用 n=3 的三元模型，n取≥4的情况较少。

4.2.2 语言模型的评价^[9]

语言模型构造完成后，如何确定好坏呢？ 目前主要有两种评价方法：

• 实用方法：通过查看该模型在实际应用（如拼写检查、机器翻译）中的表现来评价，优点是直观、实用，缺点是缺乏针对性、不够客观；
• 理论方法：迷惑度/困惑度/混乱度（preplexity），其基本思想是给测试集赋予较高概率值的语言模型较好，针对N-gram模型其计算公式如下：

由公式可知，迷惑度越小，句子概率越大，语言模型越好。使用《华尔街日报》训练数据规模为38million words构造n-gram语言模型，测试集规模为1.5million words，迷惑度如下表所示：

4.2.2 数据稀疏与平滑技术^[9]

大规模数据统计方法与有限的训练语料之间必然产生数据稀疏问题，导致零概率问题，符合经典的zip'f定律。如IBM, Brown：366M英语语料训练trigram，在测试语料中，有14.7%的trigram和2.2%的bigram在训练语料中未出现。

齐普夫定律（Zipf's Law）：一个词在一个有相当长度的语篇中的等级序号（该词在按出现次数排列的词表中的位置，他称之为rank，简称r）与该词的出现次数（他称为frequency，简称f）的乘积几乎是一个常数（constant，简称C）。用公式表示，就是 r × f = C 。（此处的C一般认为取0.1） 　　
Zipf定律是文献计量学的重要定律之一，它和罗特卡定律、布拉德福定律一起被并称为文献计量学的三大定律。
齐普夫（Zipf）定律是由美国学者G.K.齐普夫于20世纪40年代提出的词频分布定律。1932年,哈佛大学的语言学专家Zipf在研究英文单词出现的频率时,发现如果把单词出现的频率按由大到小的顺序排列,则每个单词出现的频率与它的名次的常数次幂存在简单的反比关系，这种分布就称为Zipf定律,它表明在英语单词中,只有极少数的词被经常使用,而绝大多数词很少被使用.实际上,包括汉语在内的许多国家的语言都有这种特点。
这个定律后来在很多领域得到了同样的验证，包括网站的访问者数量、城镇的大小和每个国家公司的数量。 相信你一定听过这样的说法：80%的财富集中在20%的人手中，80%的用户只使用20%的功能，20%的用户贡献了80%的访问量，也就是著名的“二八原则”。

数据稀疏问题定义：“The problem of data sparseness, also known as the zero-frequency problem arises when analyses contain configurations that never occurred in the training corpus. Then it is not possible to estimate probabilities from observed frequencies, and some other estimation scheme that can generalize (that configurations) from the training data has to be used. —— Dagan”。

人们为理论模型实用化而进行了众多尝试与努力，诞生了一系列经典的平滑技术，它们的基本思想是“降低已出现n-gram条件概率分布，以使未出现的n-gram条件概率分布非零”，且经数据平滑后一定保证概率和为1，，详细如下：

• Add-one（Laplace） Smoothing

加一平滑法，又称拉普拉斯定律，其保证每个n-gram在训练语料中至少出现1次。

unigram的最大似然估计的概率值是

其中

是语料库中的总词数（# word tokens）。unigram的Add-1平滑概率为

^[10]：

其中

是词表的大小（# word types）。

bigram的最大似然估计的概率值是：

bigram的Add-1 平滑概率为^[11]：

其中

是词表的大小（# word types）。

推广到一般情况的n-gram的语言模型中，根据极大似然估计，我们可以基于n-gram出现的频率来计算词语的概率：

n-gram的Add-1 平滑概率为^[11]：

其中

是词表的大小（# word types）。

例如，对于句子 the rat ate the cheese ，我们可以来试着计算一下经add-1平滑后的 P(ate|rat)以及 P(ate|cheese)，即

在这个例子中，

是语料库中的词汇量，而这个词汇量是不包括的，但却需要包括

^[11]。

如此一来，训练语料中未出现的n-Gram的概率不再为 0，而是一个大于 0 的较小的概率值。Add-one 平滑算法确实解决了我们的问题，但显然它也并不完美。在

时，即训练语料库中绝大部分n-gram未出现的情况（一般都是如此），Add-one Smoothing后有些“喧宾夺主”的现象，由于训练语料中未出现n-Gram数量太多，平滑后，所有未出现的n-Gram占据了整个概率分布中的一个很大的比例。因此，在NLP中，Add-one给训练语料中没有出现过的 n-Gram 分配了太多的概率空间。此外，认为所有未出现的n-Gram概率相等是否合理其实也值得商榷。而且，对于出现在训练语料中的那些n-Gram，都增加同样的频度值，这是否欠妥，我们并不能给出一个明确的答案

^[11]。

在自然语言处理中，还有其他平滑方法具体可以参考文献^[11][12][13]。

4.3 神经网络语言模型

神经网络语言模型也是统计语言模型中的一种，我们知道统计语言模型的表达是求解如下概率函数：

然而，在机器学习领域有一种通用的招数是这样的：对所考虑的问题建模后先为其构造一个目标函数，然后对这个目标函数进行优化，从而求得一组最优的参数，最后利用这组最优参数对应的模型来进行预测。

对于统计语言模型而言，利用最大似然，可把目标函数设为：

其中

表示语料 （Corpus),

表示词

的上下文（Context），即

周边的词的集合。当

为空时，就取

。特别地，对于前面介绍的 n-gram 模型，就有

，这里我们定义

。

当然，实际应用中常采用最大对数似然，即把目标函数设为

然后对这个函数进行最大化。概率

已被视为关于

和

的函数，即

其中

为待定参数集。这样一来，一旦对上公式进行优化得到最优参数集

后，

也就唯被确定了，以后任何概率

就可以通过函数

来计算。了与 n-gram 相比，这种方法不需要（事先计算并）保存所有的概率值，而是通过直接计算来获取，且通过选取合适的模型可使得

中参数的个数远小于 n-gram 中模型参数的个数。

很显然，对于这样一种方法，最关键的地方就在于函数 F 的构造了。下一小节将介绍种通过神经网络来构造 F 的方法。之所以特意介绍这个方法，是因为它可以视为 word2vec 中算法框架的前身或者说基础。

4.3.1 前向神经网络语言模型

前向神经网络，又被称为全连接（Fully Connected Neural Network）神经网络，是最早被引入到语言建模中的神经网络结构。2003年 Bengio 提出^[14]，神经网络语言模型( neural network language model, NNLM)的思想是提出词向量（word Vector）的概念，代替 ngram 使用的离散变量(高维)，采用连续变量(具有一定维度的实数向量)来进行单词的分布式表示，解决了维度灾难和数据稀疏性的问题，同时通过词向量可获取词之间的相似性。

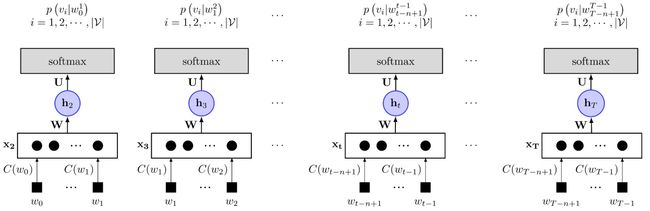
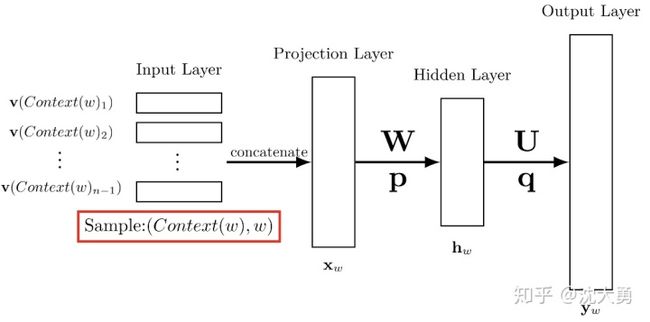
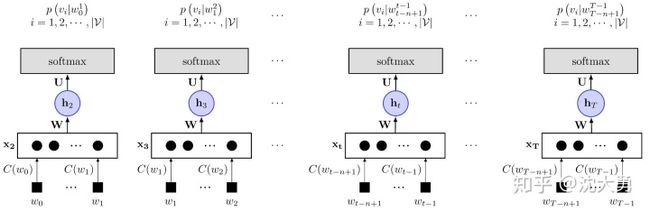
图1 前馈神经网络的模型

图1 所示的是Bengio提出的前馈神经网络的模型。它包括四个层：输人（Iput）层、投影（Projection）层、隐藏（Hidden）层和输出（Output）层，在图1中显示的不是太清楚，具体我们可以看图2。其中

,

分別为投影层与隐藏层以及隐藏层和输出层之间的权值矩阵，

,

分别为隐藏层和输出层上的偏置向量

^[15]。

图2 神经网络模型示意图

当提及文 ^[14]中的神经网络时，人们更多将其视为如图3 所示的三层结构。本文将其描述为如图2所示的四层结构，一方面是便于描述，另一方面是便于和 word2vec 中使用的网络结构进行对比。

图3 三层神经网络模型

作者在文 ^[14]中还考虑了投影层和输出层的神经元之问有边相连的情形，因而也会多出一个相应的权值矩阵，本文忽略了这种情形，但这并不影响对算法本质的理解。在数值实验中，作者发现引入投影层和输出层之问的权值矩阵虽然不能提高模型效果，但可以减少训练的迭代次数。

具体在内部的计算过程如图4所示。

图 4 前馈神经网络语言模型内部计算过程图

建立语言模型的首要工作是从训练数据集中构建词典

，并为每个词赋予唯一的索引，然后构建特征矩阵

，其中

为词典的大小，

为特征向量的大小。特征矩阵

的每行为对应词的特性向量，即词向量，通过词的索引进行查找。在训练中，对于语料

中的任意一个词

将

取为其前面的 n-1 个词（类似于 n-gram）这样二元对

就是一个训练样本了，接下来，讨论样本

经过如图 4所示的神经网络时是如何参与运算的。注意，一旦语料

和词向量长度

给定后，投影层和输出层的规模就确定了，前者为

，后者为

即语料

的词典大小而隐藏层的规模

是可调参数由用户指定。

为什么投影层的规模是（n-1) m 呢？因为输入层包含

中 n-1 个词的词向量，而投影层的向量

是这样构造的：将输入层的 n-1 个词向量按

顺序首尾相接地拼起来形成一个长向量，其长度当然就是

了，有了向量

，接下来的计算过程就很平凡了，具体为

其中 tanh 为双曲正切函数，用来做隐藏层的激活函数，上式中，tanh 作用在向量上表示它用在向量的每一个分量上。

有读者可能要问：对于语料中的一个给定向子的前几个词，其前面的词不足 m-1 个怎么办？此时，可以人为地添加一个（或几个）填充向量就可以了，它们也参与训练过程

经过上述两步计算得到的

只是一个长度为

的向量，其分量不能表示概率。如果想要

的分量

表示当上下文为

时下一个词恰为词典

中第 i 个词的概率，则还需要做一个 softmax 归一化，归一化后，

就可以表示为

其中

表示词

在词典

中的索引。上述公式给出了概率

的函数表示，即找到了上一小节中提到的函数

，那么其中待确定的参数

有哪些呢？总结起来，包括两部分

• 词向量：
• 神经网络参数：
  ,
  ，
  ，

这些参数均通过训练算法得到。值得一提的是，通常的机器学习算法中，输入都是已知的，而在上述神经概率语言模型中，输入

也需要通过训练才能得到。

接下来，简要地分析一下上述模型的运算量。在如图 2 所示的神经网络中，投影层、隐藏层和输出层的规模分别为

，

，

依次看看其中涉及的参数：

1. n 是一个词的上下文中包含的词数，通常不超过 5;
2. m 是词向量长度，通常是
   量级
3. 由用户指定，通常不需取得太大，如
   量级
4. 是语料词典的大小，与语料相关，但通常是
   量级，汉语的规模是20万个词，量级大概是
   。

再结合上述两个公式，不难发现，整个模型的大部分计算集中在隐藏层和输出层之间的矩阵向量运算，以及输出层上的 softmax 归一化运算。因此后续的相关研究工作中，有很多是针对这一部分进行优化的，其中就包括了 word2vec 的工作。

与n-gram模型相比，神经概率语言模型有什么优势呢？主要有以下两点。

1. 词语之间的相似性可以通过词向量来体现

举例来说，如果某个（英语）语料中 S1=“A dog is running in the room”出现了 10000 次，而 S2=“A cat is running in the roon”只出现了 1 次。按照 n-pramn 模型的做法，P (S1) 肯定会远大于（S2）。注意，S1 和 S2 的唯一区別在于 dog 和 cat，而这两个词无论是句法还是语义上都扮演了相同的角色，因此，p (S1) 和 p (S2) 应该很相近才对。

然而，由神经概率语言模型算得的p (S1) 和 p (S2)是大致相等的。原因在于：(1) 在神经概率语言模型中假定了“相似的”的词对应的词向量也是相似的：(2) 概率函数关于词向量是光滑的，即词向量中的一个小变化对概率的影响也只是一个小变化。这样一来，对于下面这些句子

• A dog is running in the room
• A cat is running in the room
• The cat is running in a room
• A dog is walking in a bedroom
• The dog was walking in the room

只要在语料库中出现一个，其他句子的概率也会相应地增大。

2. 基于词向量的模型自带平滑化功能

由

，不再需要像 n-gram 那样进行额外处理了。

最后，我们回过头来想想，词向量在整个神经概率语言模型中扮演了什么角色呢？训练时，它是用来帮助构造目标函数的辅助参数，训练完成后，它也好像只是语言模型的一个副产品。但这个副产品可不能小觑，下一小节将对其作进一步阐述。

3.PPL比较^[16]

实验数据显示前向神经网络语言模型的PPL远低于3-gram语言模型，体现了神经网络语言模型的优越性。

4.3.2 词向量的理解

通过上一小节的讨论，相信大家对词向量已经有一个初步的认识了。接下来，对词向量做进一步介绍。在 NLP 任务中，我们将自然语言交给机器学习算法来处理，但机器无法直接理解人类的语言，因此首先要做的事情就是将语言数学化，如何对自然语言进行数学化呢？词向量提供了一种很好的方式。

一种最简单的词向量是 one- hot representation，就是用一个很长的向量来表示一个词，向量的长度为词典

的大小

，向量的分量只有一个 1，其它全为 0，1 的位置对应该词在词典中的索引。但这种词向量表示有一些缺点，如容易受维数灾难的困扰，尤其是将其用于 Deep Learning 场景时；又如，它不能很好地刻画词与词之间的相似性。

另一种词向量是 Distributed Representation，它最早是 Hinton 于 1986 年提出的^[17]，可以克服 one-hot representation 的上述缺点。其基本想法是：通过训练将某种语言中的每一个词映射成一个固定长度的短向量（当然这里的“短”是相对于 one-hot representation 的“长”而言的），所有这些向量构成一个词向量空间，而每一向量则可视为该空间中的一个点，在这个空间上引入“距离”，就可以根据词之间的距离来判断它们之间的（词法、语义上的）相似性了。Word2vec 中采用的就是这种 Distributed Representation 的词向量。

为什么叫做 Distributed Representation？很多人问到这个题。我的一个理解是这样的：对于 one-hot representation，向量中只有一个非零分量，非常集中（有点孤注一掷的感觉）；而对于 Distributed Representation，向量中有大量非零分量，相对分散（有点风险平推的感觉），把词的信息分布到各个分量中去了。这一点，跟并行计算里的分布式并行很像。

为更好地理解上述思想，我们来举一个通俗的例子。

例 假设在二维平面上分布有 a 个不同的点，给定其中的某个点，现在想在平面上找到与这个点最相近的一个点我们是怎么做的呢？首先，建立一个直角坐标，基于该坐标条，其上的每个点就唯一地对应一个坐标（x,y）；接着引入欧氏距离；最后分別计算这个点与其他 a-1 个点之问的距离，对应最小距离值的那个（或那些）点便是我们要找的点了。

上面的例子中，坐标（x, y）的地位就相当于词向量，它用来将平面上一个点的位置在数学上作量化。坐标系建立好以后，要得到某个点的坐标是很容易的。然而，在 NLP 任务中，要得到词向量就复杂得多了，而且词向量并不唯一，其质量依赖于训练语料、训练算法等因素

如何获取词向量呢？有很多不同模型可用来估计词向量，包括有名的 LSA (Latent Semantic Analysis）和 LDA (Latent Dirichlet Allocation）。此外，利用神经网络算法也是一种常用的方法，上一小节介绍的神经概率语言模型就是一个很好的实例。当然，在那个模型中，目标是生成语言模型，词向量只是一个副产品。事实上，大部分情况下，词向量和语言模型都是捆绑在一起的，训练完成后两者同时得到。用神经网络来训练语言模型的思想最早由百度 IDL（深度学习研究院）的徐伟^[18]提出。这方画最经典的文章要数 Bengio 于 2003 年发表在 JMLR 上的《A Neural Probabilistic Language Model》，其后有一系列相关的研究工作，其中也包括谷歌 Tomas Nikolov 团队的 word2vec。

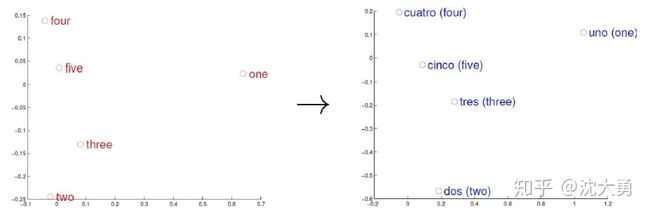
图5 五个词在两个向量空间中的位置（左：E，右：S）

文献中^[19]给出一个简单的例子可以帮助我们了解词向量，考虑英语和西班牙语两种语言，通过训练分别得到它们对应的词向量空间 E (nglish）和S (panish）。从英语中取出五个词 one, two, three, four, five，设其在 E 中对应的词向量分别为

为方便作图，利用主成分分析（PCA）降维，得到相应的二维向量

，在二维平面上将这五个点描出来，如图5左图所示。

类似地，在西班牙语中取出（与 one, two, three, four, five 对应的）uo, dos, tres, cuatro,cinco，设其在 S 中对应的词向量分别为

,用 PCA 降维后的二维向量分别为

将它们在二维平面上描出来（可能还需作适当的旋转），如图4右图所示。

观察左、右两幅图，容易发现：五个词在两个向量空间中的相对位置差不多，这说明两种不同语言对应向量空间的结构之间具有相似性，从而进一步说明了在词向量空间中利用距离刻画词之间相似性的合理性。

注意，词向量只是针对“词”来提的，事实上，我们也可以针对更细粒度或更粗粒度来进行推广，如字向量^[20]，句子向量和文档向量^[21]，它们能为字、句子、文档等单元提供更好的表示。

其他一些好的博客可以参考^[22][23]。

致谢

本文撰写借鉴和复用了参考文献里面的大量的表述，在这里一并说明，此文的撰写仅仅是为了自己方便检索回忆。

参考

1. ^On word embeddings - Part 1 https://ruder.io/word-embeddings-1/index.html
2. ^漫谈词向量 https://www.sohu.com/a/117691542_355135
3. ^A brief history of word embeddings/ https://www.gavagai.se/blog/2015/09/30/a-brief-history-of-word-embeddings/
4. ^^abType/Token Ratios and the Standardised Type/Token ratio http://www.lexically.net/downloads/version5/HTML/index.html?type_token_ratio_proc.htm
5. ^神经网络语言建模系列之一：基础模型 https://www.jianshu.com/p/a02ea64d6459
6. ^自然语言处理之语言模型（LM） https://blog.csdn.net/qq_36330643/article/details/80143960
7. ^Language Model https://web.stanford.edu/class/cs124/lec/languagemodeling.pdf
8. ^A Bit of Progress in Language Modeling Extended Version https://arxiv.org/pdf/cs/0108005.pdf
9. ^^ab语言模型 https://blog.csdn.net/xiaokang06/article/details/17965965
10. ^smoothing backoff http://www.cs.cornell.edu/courses/cs4740/2014sp/lectures/smoothing+backoff.pdf
11. ^^abcde自然语言处理中N-Gram模型的Smoothing算法 https://blog.csdn.net/baimafujinji/article/details/51297802
12. ^NLP Lunch Tutorial: Smoothing https://nlp.stanford.edu/~wcmac/papers/20050421-smoothing-tutorial.pdf
13. ^Maximum Likelihood and Smoothing https://people.cs.umass.edu/~dasmith/inlp2009/lect5-cs585.pdf
14. ^^abcBengio, Y., Ducharme, R., Vincent, P., & Janvin, C. (2003). A Neural Probabilistic Language Model. The Journal of Machine Learning Research, 3, 1137–1155. Retrieved from http://www.jmlr.org/papers/volume3/bengio03a/bengio03a.pdf
15. ^word2vec 中的数学原理详解（三）背景知识 https://blog.csdn.net/itplus/article/details/37969817
16. ^神经网络语言建模系列之一：基础模型 https://www.jianshu.com/p/a02ea64d6459
17. ^Learning distributed representations of concepts https://pdfs.semanticscholar.org/cef4/692d7d5f33b0d819079642c69778497415e6.pdf
18. ^Can Artificial Neural Networks Learn Language Models http://www.speech.cs.cmu.edu/Communicator/papers/01291.pdf
19. ^Exploiting Similarities among Languages for Machine Translation https://arxiv.org/abs/1309.4168
20. ^Deep Learning for Chinese Word Segmentation and POS Tagging https://www.aclweb.org/anthology/D13-1061.pdf
21. ^Distributed Representations of Sentences and Documents https://arxiv.org/abs/1405.4053
22. ^Deep Learning in NLP （一）词向量和语言模型 http://licstar.net/archives/328#s20
23. ^NLP之——Word2Vec详解 https://www.cnblogs.com/guoyaohua/p/9240336.html