学习笔记——简单的DFS（深搜）思考

深度优先搜索，简称DFS，是图的基本算法之一，与广度优先搜索（BFS）常常在搜索中被使用。
与广搜相比，深搜的特点是：可以更简单地对图中各路径进行搜索，这往往是需要求路径种类的突破口。

深搜的基本思路如下：
1.寻找某一顶点，以该顶点为起点。
2.从起点往某一方向出发，在经过某个点后，对该点进行标记（你可以比作“到此一游”，下次看到就不用来这里了，毕竟已经来过了，当然涉及路径不同的部分情况，实际标记的是路线而不只是点），再往未被标记的点前进，继续深度搜索，直至图中可行的点都被访问过。
3.如还有未被访问的点，则选取未被访问过的点，从步骤1开始，直至所有点都被访问过。

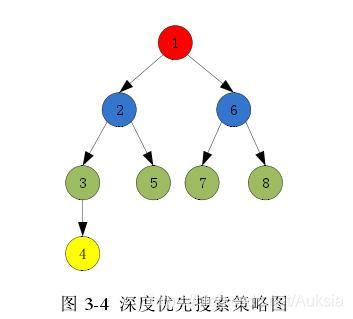
如上图，顶点为1，你可以从1开始，优先从左侧端点开始探索，则路径为1 -> 2 -> 3 -> 4，此时4没有子节点了，就返回上一级3，发现除了4没有其他子节点，继续返回上一级2，继续向下搜索到5…不断搜索，直至把所有可能性搜完。当然，在这你也可以从4开始搜，4 -> 3 -> 2 -> 1 -> 6 -> 8这样的顺序也不妨一试。

深搜（DFS）的模板大致如下：

int vis[MAXN][MAXN]; //对该数列进行搜索
int jud[MAXN][MAXN]; //用于判断是否走过了
int n,m; //图的长、宽
int dx[5] = {
     0,1,0,-1,0}; //两个数组竖着看，往某个方向搜索一个单位
int dy[5] = {
     0,0,1,0,-1};
void DFS(int x, int y){
      // 特别注意，这里x指行，y指列，写反问题就大了orz
		if(不符合x的条件) //例如碰到图的边缘就返回上一级
			return; //返回上一级
		if(不符合y的条件)
			return；//返回上一级
		if(vis[x][y]==-1) // 假设碰到障碍的值设为-1
			return; //返回上一级
		if(满足条件（如搜到终点）){
     
			ans++; //满足条件答案增加，例如讨论路径种类
			return; //搜到终点赶紧往回跑路，退回上一级
		}
		jud[x][y] = 1; //表示“到此一游”，标记已访问
		for(int i=1;i<=4;i++){
     
			int nx,ny;
			nx = x+dx[i]; //x或y的坐标改变一个单位，即移动一个单位
			ny = y+dy[i];
			DFS(nx,ny);	//搜索下一个点
			//jud[x][y] = 0;
			//以上一行为回溯，根据实际情况判断是否需要加上
			//在下文会解释什么时候需要用回溯
		}
	}

下面的题可以拿来试试手~~
洛谷P1605 迷宫
题目背景
给定一个N*M方格的迷宫，迷宫里有T处障碍，障碍处不可通过。给定起点坐标和终点坐标，问: 每个方格最多经过1次，有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

输入格式
第一行N、M和T，N为行，M为列，T为障碍总数。第二行起点坐标SX,SY，终点坐标FX,FY。接下来T行，每行为障碍点的坐标。

输出格式
给定起点坐标和终点坐标，问每个方格最多经过1次，从起点坐标到终点坐标的方案总数。

输入输出样例
输入
2 2 1
1 1 2 2
1 2
输出
1

【数据规模】
1≤N,M≤5

魔鬼画手凑合看哈哈哈
像这样搜索，从1->4->7再向下就出边界了，于是返回上一级，即点7，再进行其他方向的尝试。代码如下：

#include //万能头，也可手写头文件
using namespace std;
int n,m,t; //迷宫长宽和障碍物数量 
int sx,sy,fx,fy; //起点x y坐标，终点x y坐标
int obx,oby; // 障碍物的坐标

int vis[6][6]; //用于搜索路径
int ans = 0; 
int dx[5] = {
     0,1,0,-1,0}; //搜索的上下左右方向
int dy[5] = {
     0,0,1,0,-1};
void dfs(int x,int y) {
      //用x来表示x坐标，y来表示y坐标
	if(x<1 || x>n)	return; //超出图的边缘即返回上一个点，换方向走
	if(y<1 || y>m)	return;
	if(vis[x][y]==-1 || vis[x][y]==1)	return; //若撞到障碍物或者碰到走过的点，换方向走
	if(x==fx && y==fy) {
      //若走到终点，则路径+1，同时回去上一级换方向走
		ans++;
		return;
	}
	//判断条件优先写，写完再标记，以免出现错误
	vis[x][y] = 1; //走过就随手标记
	for(int i=1; i<=4; i++) {
      //往某个方向一直走，走到尽头就换方向
		int nx,ny;
		nx = x+dx[i]; //往某个方向一个单位
		ny = y+dy[i];
		dfs(nx,ny);
	}
		vis[x][y] = 0; //回溯，防止下一次走新方案的时候，无法来到这个点
}
int main() {
     
	scanf("%d %d %d",&n,&m,&t); //注意此处n为行，m为列 
	scanf("%d %d %d %d",&sx,&sy,&fx,&fy); //输入起点终点坐标
	for(int i=1; i<=t; i++) {
     
		scanf("%d %d",&obx,&oby); //输入障碍物坐标
		vis[obx][oby] = -1; //标记障碍物位置，便于搜索的时候判断
	}
	dfs(sx,sy); //从起点开始搜索
	printf("%d",ans); //输出路径方案总数
	return 0;
}

再在这里讲讲一般什么时候需要回溯：
1. 与路径的不同相关（如计算路径方案）
2. 被标记的点会影响下一步或未来某一步的搜索

至于什么时候用BFS（广搜），什么时候用DFS（深搜），我的建议是：
涉及最短距离就用BFS，涉及路径就用DFS。
具体情况具体分析吧。

顺手贴张图。

如有出错 希望有大佬帮忙指正。
以上。
（我太菜了，下次再更新点新东西吧QAQ）