leetcode笔记总结——(6)通过四道题,来掌握二叉树的层序遍历。(python3和C++实现)
目录
- 第一题:
- 1.1 题目描述:
- 1.2 思路:
- 1.3 代码:
- (1)python代码:
- (2)C++代码:
- 第二题:
- 2.1 题目描述:
- 2.2 思路:
- 2.3 代码:
- (1)python代码:
- (2)C++代码:
- 第三题:
- 3.1 题目描述:
- 3.2 思路:
- 3.3 代码:
- (1)python代码:
- (2)C++代码:
- 第四题:
- 4.1 题目描述:
- 4.2 思路:
- 4.3 代码:
- (1)python代码:
- (2)C++代码:
通过四道题,来掌握二叉树的层序遍历。说明一下,要对节点类和树类熟悉,这里有一个教程:https://blog.csdn.net/weixin_45901519/article/details/115224790
第一题:
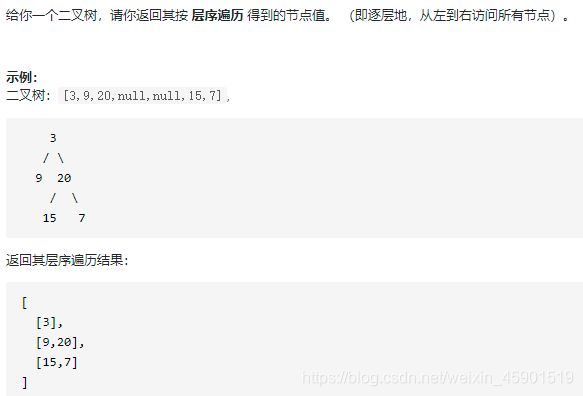
1.1 题目描述:
1.2 思路:
利用广度优先遍历BFS,一层一层的进行查看,思路如下:
- 1、如果是空子树,直接返回[];
- 2、有根节点,则首先根结点入队列queue,queue里装的是当前层的所有结点,开始遍历;
- 3、把当前层queue中的结点的值保存到结果列表中;
- 4、遍历当前层queue的每个结点的左子结点,右子结点,入队列,最关键的地方是:把queue列表更新成当前层的孩子节点列表,直到queue为空;
- 5、最后返回res。
1.3 代码:
(1)python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root: return []
#根结点入queue
queue = [root]
res = []
while queue:
res.append([node.val for node in queue])
#存储当前层的孩子节点列表
ll = []
#对当前层的每个节点遍历
for node in queue:
#如果左子节点存在,入队列
if node.left:
ll.append(node.left)
#如果右子节点存在,入队列
if node.right:
ll.append(node.right)
#后把queue更新成下一层的结点,继续遍历下一层
queue = ll
return res
(2)C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector <vector <int>> ret; //两层vector容器存放遍历结果
if (!root) {
// 如果根节点为空,直接返回空的vector
return ret;
}
queue <TreeNode*> q;
q.push(root); //先让根节点入队
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector <int> ()); //给vector容器中插入一个空的vector容器
for (int i = 1; i <= currentLevelSize; ++i) {
auto node = q.front(); //auto就是根据后面的推断前面的类型
q.pop();
ret.back().push_back(node->val); //将vector容器中的最后一个vector取出,插入节点值
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
};
BFS都是这样的模板,记住即可。
第二题:
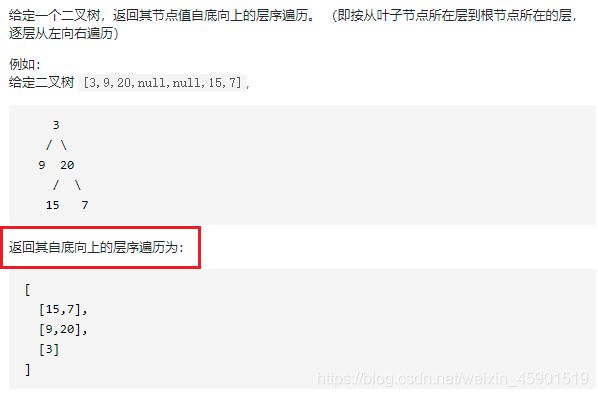
2.1 题目描述:
2.2 思路:
这个和前面的基本一样,只是在输出的时候逆序输出即可。
2.3 代码:
(1)python代码:
python在最后逆序输出的时候有两种方法:
(1)列表提供了.reverse()方法,就可以逆序了,注意改变自身,不返回值。
(2)列表切片操作:list[::-1]就可以了。
推荐使用第一种,试了一下,内存消耗和运行时间都比第二种要效果好。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if not root: # 如果二叉树为空,直接返回[]
return []
queue = [root] # 队列,并且先让根节点入队
res = [] # 储存结果的列表
while queue:
res.append([node.val for node in queue]) # 当前节点的值保存到res中
ll = [] # 保存当前队列中节点的孩子节点
for node in queue:
if node.left: # 左子树
ll.append(node.left)
if node.right:
ll.append(node.right)
queue = ll # 更新队列到下一层
res.reverse() # 逆序输出,会改变自身
return res
# return res[::-1]
(2)C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ret; //存放返回结果
if(!root)
{
return ret;
}
queue<TreeNode*> q; //队列,存放当前节点
q.push(root); //先让根节点入队
while(!q.empty())
{
ret.insert(ret.begin(), vector<int>()); //将空的vector放入ret最前面,为后续的插入做准备
int queue_len = q.size(); //记录当前q的大小,因为q可能会改变
for(int i = 0; i < queue_len;i++)
{
auto node = q.front(); // 查看队首元素
q.pop(); // 将队首元素出队
ret[0].push_back(node->val); // 将当前队首元素插入二维的ret元素中
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
};
上面的C++代码是直接在ret前面插入,但是我们知道,vector是顺序保存的,因此,在第一个位置插入时,后面的元素都要移动,也就说这样时间复杂度高了。下面代码是改进:也就是说先尾插,再在最后逆序。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ret; //存放返回结果
if(!root)
{
return ret;
}
queue<TreeNode*> q; //队列,存放当前节点
q.push(root); //先让根节点入队
while(!q.empty())
{
ret.push_back(vector<int>()); //将空的vector放入ret末尾,为后续的插入做准备
int queue_len = q.size(); //记录当前q的大小,因为q可能会改变
for(int i = 0; i < queue_len;i++)
{
auto node = q.front(); // 查看队首元素
q.pop(); // 将队首元素出队
ret.back().push_back(node->val); // 将当前队首元素插入二维的ret元素中
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
//逆序
reverse(ret.begin(), ret.end());
return ret;
}
};
运行时间和占用内存都优于第一种。
第三题:
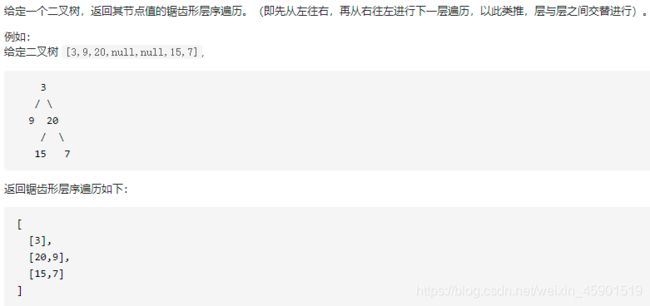
3.1 题目描述:
3.2 思路:
在使用广度优先遍历,从左到右一层一层的遍历了之后(第一题的思路),把结果列表再遍历,这次遍历时,如果下标是奇数,则反转。
3.3 代码:
(1)python代码:
注意列表在反转的时候,有两种方法:
(1)切片操作:[::-1]
(2)反转函数.reverse()(这个函数改变自身,没有返回值)
推荐第二种,因为运行速度快。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
ret = []
queue = [root] # 队列,根节点入队
while queue:
ret.append([node.val for node in queue])
level = [] # 保存当前节点的孩子节点
for node in queue:
if node.left:
level.append(node.left)
if node.right:
level.append(node.right)
queue = level
for i in range(len(ret)):
if i % 2 != 0: # 如果是奇数,则反转
ret[i].reverse() # 这个比[::-1]效果好
return ret
(2)C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret; //存放结果
if (!root) return ret;
queue<TreeNode*> q;
q.push(root);
while(q.size() != 0)
{
ret.push_back(vector<int>()); // 初始化一个元素(插在末尾)
int level_size = q.size(); //记录当前层节点的个数
for(int i = 0;i < level_size;++i)
{
auto node = q.front(); // 查看当前队头元素
q.pop(); //出队
ret.back().push_back(node->val); //插入节点的值
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
}
//奇数下标进行反转
for (int i = 0;i < ret.size();i++)
{
if (i % 2 != 0) //奇数
{
reverse(ret[i].begin(), ret[i].end()); //反转
}
}
return ret;
}
};
第四题:
4.1 题目描述:
4.2 思路:
右视图即每层最右边的值,因此只需要做一个非常简单的小变化,即返回的列表只需要对每一层的列表的最后一个元素入结果列表就可以了。
4.3 代码:
(1)python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root: return []
ret = [] # 存放结果列表
queue = [root] # 根节点入队
while queue:
ret.append([node.val for node in queue][-1]) # 保存每层的最后一个元素
level = [] # 存放下一层节点
for node in queue:
if node.left: level.append(node.left)
if node.right: level.append(node.right)
queue = level
return ret
(2)C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> ans; //存放结果
if (!root) return vector<int>(); //返回匿名对象
queue<TreeNode*> q;
q.push(root);
while(q.size() != 0)
{
int level_size = q.size();
for (int i = 0;i < level_size;++i)
{
auto node = q.front();
q.pop();
if(i == level_size-1) ans.push_back(node->val); // 只保存最后一个
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
}
return ans;
}
};
我刚开始的思路是,先遍历了再在最后面,用一个for循环取最后一个数,这个显然有点蠢。看了别人的代码,在保存的时候就判断要不要入结果列表,复杂度会降低很多。
因此,能在主程序中就判断,坚决不要再重新遍历了,什么代码都是一样。