行为目标检测ROC、AUC及相关参数是什么含义?
行为目标检测ROC、AUC及相关参数是什么含义?
1.ROC、AUC定义及相关概念
ROC : TPR - FPR 曲线
AUC : ROC 曲线下面积
TPR : TP/(TP+FN)
FPR : FP/(FP+TN)
Precision : TP / (TP + FP)
Recall: TP / (TP + FN)
IOU : (TP)/(TP+TN+FP)
TP: IoU>0.5的检测框数量(同一Ground Truth只计算一次)
FP: IoU<=0.5的检测框,或者是检测到同一个GT的多余检测框的数量
FN: 没有检测到的GT的数量
FP:
关于TP、FP、FN、FP后面有更直观更简单直观的计算方式。
2.行为目标检测从得分到AUC的详细计算过程
2.1 数据流
2.2 阈值
2.2.1 阈值threshold的影响
我们需要一个对于score的threshold, 为什么呢? 比如在一个bounding box里, 我识别出来鸭子的score最高, 可是他也只有0.1, 那么他真的是鸭子吗? 很可能他还是负样本。 所以我们需要一个阈值, 如果识别出了鸭子而且分数大于这个阈值才真的说他是正样本, 否则他是负样本。
2.2.2 阈值是如何设定的?
如下图所示,首先我们将一个视频通过滑动窗口分割得到n个小视频段,我们将n个小视频段,通过model模型,我们可以得到一个nxk的得分矩阵,每一行为对应小视频段的得分,我们取出每一行的得分的最大值,得到整个视频的得分矩阵(nx1),我们取阈值thresold = A[k] ( k = 1, 2, 3, n-1 )
图1
2.3 求pr_label(预测标签)
pr为图一最后的得分A={nx1},为了方便计算,我们将n=5;GT是已给出的视频异常数据;不妨设thresold = 0.4,大于0.4的pr_label = 1,反之 pre_label = 0。
| GT | pr | pr_label |
|---|---|---|
| 1 | 0.6 | 1 |
| 0 | 0.2 | 0 |
| 0 | 0.4 | 0 |
| 1 | 0.3 | 0 |
| 1 | 0.5 | 1 |
表1
2.4 求FP, TP, FN, TN,TPR ,FPR ,Precision ,Recall ,IOU ,F-measure
求FP, TP, FN, TN的表格如下:
| GT | pr_label | |
|---|---|---|
| FP | 0 | 1 |
| TP | 1 | 1 |
| FN | 1 | 0 |
| TN | 0 | 0 |
求表1的TP, FN, FP, TN
| GT | pr | pr_label | |
|---|---|---|---|
| 1 | 0.6 | 1 | TP |
| 0 | 0.2 | 0 | TN |
| 0 | 0.4 | 0 | TN |
| 1 | 0.3 | 0 | FN |
| 1 | 0.5 | 1 | TP |
表2
总结表2,TP = 2, FN = 1, FP = 0, TN = 2。
由公式 TPR=TP/(TP+FN)
FPR=FP/(FP+TN)
Precision=TP/(TP+FP)
Recall=TP/(TP+FN)
IOU = (TP)/(TP+TN+FP)
F-measure = 1 / ( 1/2 * ( 1/Precision + 1/Recall ))
我们可以求出 TPR = 0.67;FPR = 0;Precision = 1 ;Recall = 0.67;IOU = 0.5; F-measure = 0.8;这样我们就对于每个threshold,我们都有
(TPR , FPR )的pair 。
2.5 画ROC曲线
2.5.1 ROC的动机
对于0,1两类分类问题,一些分类器得到的结果往往不是0,1这样的标签,如神经网络得到诸如0.5,0.8这样的分类结果。这时, 我们人为取一个阈值,比如0.4,那么小于0.4的归为0类,大于等于0.4的归为1类,可以得到一个分类结果。同样,这个阈值我们可 以取0.1或0.2等等。取不同的阈值,最后得到的分类情况也就不同。
2.5.2 为什么要使用ROC曲线?
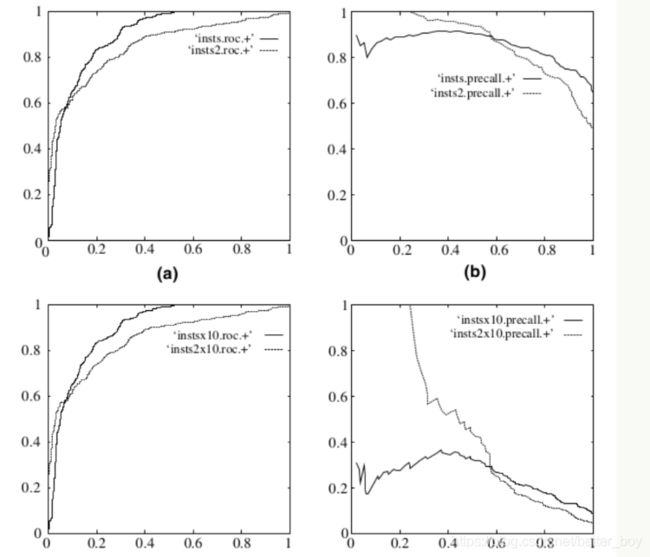
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时 候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相 反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比:
在上图中,(a)和©为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结 果,©和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,Precision- Recall曲线则变化较大。
2.5.3 ROC的定义
关于两类分类问题,原始类为positive、negative,分类后的类别为p’、n’。排列组合后得到4种结果,如下图所示:
于是我们得到四个指标,分别为:真阳、伪阳、伪阴、真阴。ROC空间将伪阳性率(FPR)定义为 X 轴,真阳性率(TPR)定义为 Y 轴。这两个值由上面四个值计算得到,公式如下:
TPR:在所有实际为阳性的样本中,被正确地判断为阳性之比率。TPR=TP/(TP+FN)
FPR:在所有实际为阴性的样本中,被错误地判断为阳性之比率。FPR=FP/(FP+TN)
放在具体领域来理解上述两个指标。如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
2.5.4 ROC曲线图形可视化
由上述2.4参数可知,我们可以根据已有数据,得出以下表格(仅仅是数据的一部分)
表3
对于每个threshold,我们都有(TPR , FPR )的pair , 也就有了TPR 和FPR 之间的curve关系。有了这么一条TPR -FPR , 他衡量着两个有价值的判断标准, TPR 和FPR 的关系, 那么不如两个一起动态考虑,我们可以得到下图的曲线(根据表3。左侧只展示了部分数据,其中FPR是根据升序排列)。
2.6 AUC值
AUC(Area Under roc Curve)是一种用来度量分类模型好坏的一个标准。
2.6.1 AUC值的定义
AUC值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
2.6.2 AUC值的物理意义
假设分类器的输出是样本属于正类的socre(置信度),则AUC的物理意义为,任取一对(正、负)样本,正样本的score大于负样本 的score的概率。
2.6.3 AUC值的计算
(1)第一种方法:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积之和,计算的精度与阈值的精 度有关。
(2)第二种方法:根据AUC的物理意义,我们计算正样本score大于负样本的score的概率。取NM(N为正样本数,M为负样本数) 个二元组,比较score,最后得到AUC。时间复杂度为O(NM)。
(3)第三种方法:与第二种方法相似,直接计算正样本score大于负样本的score的概率。我们首先把所有样本按照score排序,依次 用rank表示他们,如最大score的样本,rank=n(n=N+M),其次为n-1。那么对于正样本中rank最大的样本(rank_max),有M-1个其他 正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负 样本的概率为: