神经网络（目标为深层堆叠稀疏自动编码器网络，使用matlab自带的函数）

 

1.一个普通神经网络的训练完整代码：

感谢该网友提供的以下这块代码 https://zhidao.baidu.com/question/309976879.html

P_pix=[ 175.8728234	67	0.380957096	0.270238095

        149.5075249	113	0.7558148	0.370238095
        155.1104445	145	0.934817771	0.46547619
        151.5008251	95	0.627059291	0.610714286
        163.4778272	60	0.36702225	0.754761905
        219.5723116	72	0.327910197	0.257142857
        176.356725	119	0.674768711	0.351190476
        139.7621988	185	1.323676942	0.489285714
        162.3837191	126	0.775939858	0.642857143
        175.2430455	70	0.399445238	0.742857143
        207.9933893	98	0.471168821	0.280952381
        140.0357097	116	0.828360139	0.357142857
        139.3646297	131	0.939980254	0.48452381
        138.1828499	125	0.904598509	0.632142857
        175.5874268	67	0.381576296	0.741666667];
t=[1 0 0;1 1 0; 0 1 0; 0 1 1; 0 0 1;1 0 0;1 1 0; 0 1 0; 0 1 1; 0 0 1;1 0 0;1 1 0; 0 1 0; 0 1 1; 0 0 1];
t_train=t';
P_train=P_pix';
P_min_max=minmax(P_train);
for n1=1:15
           P_train(1,n1)=(P_train(1,n1)-P_min_max(1,1))/(P_min_max(1,2)-P_min_max(1,1));
           P_train(2,n1)=(P_train(2,n1)-P_min_max(2,1))/(P_min_max(2,2)-P_min_max(2,1));
end
net = newff(minmax(P_train),[17,3],{'tansig','logsig'},'trainbfg');

net=init(net);
net.trainparam.epochs=5000;
net.trainparam.show=1000
net.trainparam.goal=1e-7;
net=train(net,P_train,t_train);
P_pix_n=[169.0473307	72	0.42591622	0.25952381
        142.1908928	126	0.886132702	0.371428571
        148.982568	128	0.859160919	0.50952381
        148.5	96	0.646464646	0.60952381
        167.002994	68	0.407178329	0.742857143];
P_pix_n=P_pix_n';
for n1=1:5
           P_pix_n(1,n1)=(P_pix_n(1,n1)-P_min_max(1,1))/(P_min_max(1,2)-P_min_max(1,1));
           P_pix_n(2,n1)=(P_pix_n(2,n1)-P_min_max(2,1))/(P_min_max(2,2)-P_min_max(2,1));
end
sim(net,P_pix_n)

结果是
ans =

    1.0000    0.9789    0.0002    0.0000    0.0000
    0.0282    1.0000    1.0000    0.9999    0.0000
    0.0000    0.0000    0.0056    0.9998    1.0000

 

2. 查看训练完成的权值和偏置代码

感谢：https://zhidao.baidu.com/question/1609659045598691947.html

一般情况下net.IW{1,1}就是输入层和隐含层之间的权值。
如果网络是单隐含层，net.lw{2,1}就是输出层和隐含层之间的权值。
可以如此记忆，输入层为代号1，第一隐层为代号1，第二隐层为代号2，输出层为代号3。以此类推，
 

IW规定的是输入层与第一隐层的权值 IW{1,1} 方向为，第二代号到第一代号的权值，也就是第一隐层到输入层权值，该值为矩阵17*4。LW代表第一隐层直至输出层的情况，LW{2,1}即指第二隐层到第一隐层的权值，此处因为只有一个隐层，整体网络结构为4*17*3， 4为输入维数，17为中间隐层维数，3为输出维数，所以LW{2,1}表示输出层到第一隐层的权值，即3*17。稍微解释1中代码的newff 的参数：

偏置很好理解net.b{1}就是输入层到第一隐层的偏置，以此类推。

net = newff(minmax(P_train),[17,3],{'tansig','logsig'},'trainbfg');
minmax(P_train)：输出归一化后的每个最大值和最小值，此处按行求最大值和最小值。也即每个属性的最大值和最小值。

[17,3] ：代表隐层到输出层的维数，注意包含输出层，输入层不需要指明。17为第一隐层数，3为输出层数
{'tansig','logsig'} ： 此处为第一隐层到输出层的激活函数。即第一隐层为tansig，输出层为‘logsig’从训练得截图也可得出。

 

trainbfg' ： 为训练方法。

 

3.如何让历史重现？--需要在train函数前对net.iw,net.lw,net.b{1},net.b{2}进行赋值

net = newff(minmax(P_train),[17,3],{'tansig','logsig'},'trainbfg');
%net=init(net);此函数主要功能是随机初始化权值和偏置

net.iw{1,1}=net.iw{1,1}; %此函数是将上次训练好后的权值赋值给这次训练的权值，运行时你会发现并不训练，因为之前已经训练好了，所以你

%用训练好后的权值就会使程序不运行，因为达到截止要求。这里主要是为堆叠稀疏自动编码器做准备，因为有微调，所以肯定最终的效果，还是

%会进行训练。

首先需要在train 函数后面保存上次运行后的权值和偏置，为了复现历史结果，需要，在下次的train 函数前面去掉init函数，然后在train 函数前面添加之前训练后的权值。由于已经达到误差要求，所以运行程序并不进行训练。从而保证结果的可复现性。

net.lw{2,1}=net.lw{2,1};
net.b{1}=net.b{1};

 

net.b{2}=net.b{2};

net=train(net,P_train,t_train);

4.一个简单的针对分类问题的深度堆叠稀疏自动编码器代码：http://ww2.mathworks.cn/help/nnet/ug/construct-deep-network-using-autoencoders.html

直接在matlab运行下述命令，就能打开实例代码：

 

 

openExample('nnet/ConstructDeepNetworkUsingAutoencodersExample')

 

%% Construct Deep Network Using Autoencoders

% Load the sample data.

% Copyright 2015 The MathWorks, Inc.

[X,T] = wine_dataset;
%%
% Train an autoencoder with a hidden layer of size 10 and a linear transfer
% function for the decoder. Set the L2 weight regularizer to 0.001,
% sparsity regularizer to 4 and sparsity proportion to 0.05.
hiddenSize = 10;
autoenc1 = trainAutoencoder(X,hiddenSize,...
    'L2WeightRegularization',0.001,...
    'SparsityRegularization',4,...
    'SparsityProportion',0.05,...
    'DecoderTransferFunction','purelin');
%%
% Extract the features in the hidden layer.
features1 = encode(autoenc1,X);
%%
% Train a second autoencoder using the features from the first autoencoder. Do not scale the data.
hiddenSize = 10;
autoenc2 = trainAutoencoder(features1,hiddenSize,...
    'L2WeightRegularization',0.001,...
    'SparsityRegularization',4,...
    'SparsityProportion',0.05,...
    'DecoderTransferFunction','purelin',...
    'ScaleData',false);
%%
% Extract the features in the hidden layer.
features2 = encode(autoenc2,features1);
%%
% Train a softmax layer for classification using the features, |features2|,
% from the second autoencoder, |autoenc2|.
softnet = trainSoftmaxLayer(features2,T,'LossFunction','crossentropy');
%%
% Stack the encoders and the softmax layer to form a deep network.
deepnet = stack(autoenc1,autoenc2,softnet);
%%
% Train the deep network on the wine data.
deepnet = train(deepnet,X,T);
%%
% Estimate the wine types using the deep network, |deepnet|.
wine_type = deepnet(X);
%%
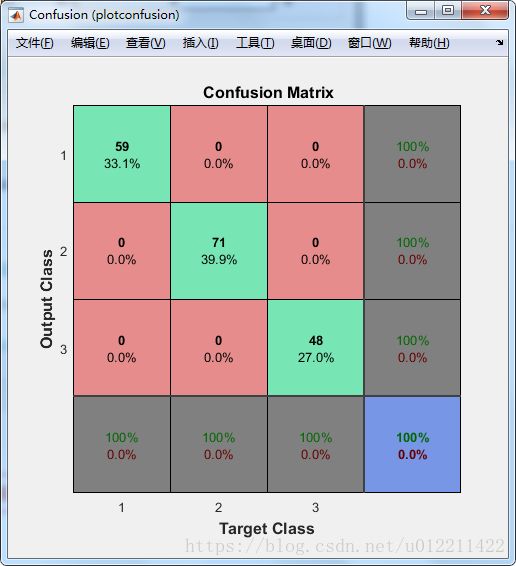
% Plot the confusion matrix.

 

 

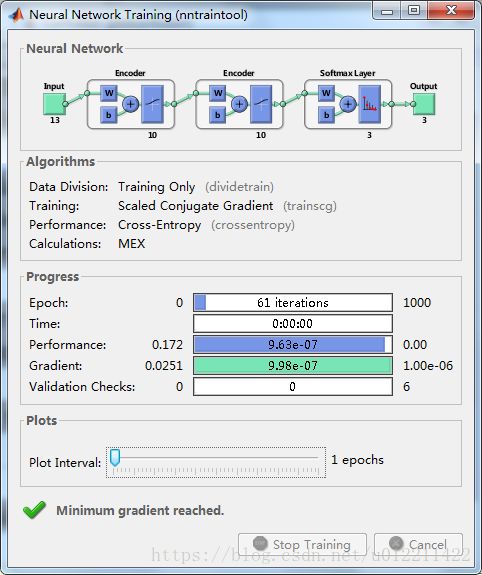
plotconfusion(T,wine_type);

 

运行此代码可以出现上述两张图片。

5.当遇到回归问题，好像实例并不能为我们解决，此时就需要手动堆叠训练深度堆叠自动编码器。

下面简单的构建一个回归模型，例子不太好还是用2中的分类问题，所以大家不要太见怪，自己改改数据集就行。

该数据集的输入变量为13*178，输出变量为3*178，也就是输入维数为13，输出维数为3，样本个数为178。具体还要仔细查阅。比如分训练集和测试集之类的，此处只有训练集。

%% Construct Deep Network Using Autoencoders
% Load the sample data.


% Copyright 2015 The MathWorks, Inc.


[X,T] = wine_dataset;


P_train = X;
P_min_max=minmax(X);
for ml =1:13
    for n1=1:178
           P_train(1,n1)=(P_train(ml,n1)-P_min_max(ml,1))/(P_min_max(ml,2)-P_min_max(ml,1));
    end
end


%%
% Train an autoencoder with a hidden layer of size 10 and a linear transfer
% function for the decoder. Set the L2 weight regularizer to 0.001,
% sparsity regularizer to 4 and sparsity proportion to 0.05.
hiddenSize = 10;
autoenc1 = trainAutoencoder(P_train,hiddenSize,...
    'L2WeightRegularization',0.001,...
    'SparsityRegularization',4,...
    'SparsityProportion',0.05,...
    'DecoderTransferFunction','purelin',...
     'ScaleData',false);


%%
% Extract the features in the hidden layer.
features1 = encode(autoenc1,X);
%%
% Train a second autoencoder using the features from the first autoencoder. Do not scale the data.
hiddenSize = 10;
autoenc2 = trainAutoencoder(features1,hiddenSize,...
    'L2WeightRegularization',0.001,...
    'SparsityRegularization',4,...
    'SparsityProportion',0.05,...
    'DecoderTransferFunction','purelin',...
    'ScaleData',false);


%%
% Extract the features in the hidden layer.
features2 = encode(autoenc2,features1);
%%
% Train a deep model--finetuning,


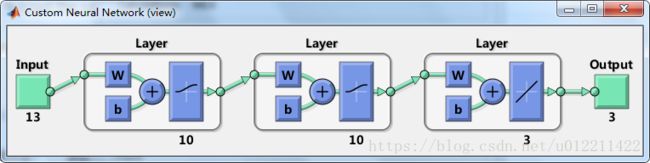
net = newff(minmax(P_train),[10,10,3],{'logsig','logsig','purelin'},'trainscg');
net.iw{1,1}=autoenc1.EncoderWeights;
net.lw{2,1}=autoenc2.EncoderWeights;
net.b{1}=autoenc1.EncoderBiases;
net.b{2}=autoenc2.EncoderBiases;
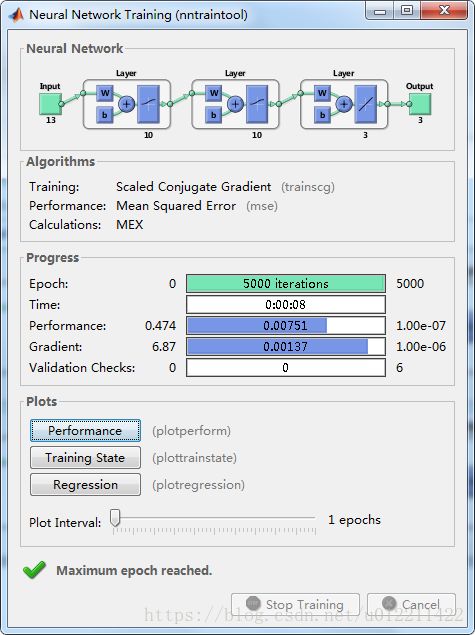
net.trainparam.epochs=5000;
net.trainparam.show = 1000;
net.trainparam.goal=1e-7;
net=train(net,P_train,T);
view(net)
T_predicted = sim(net,P_train);