卷积、池化
卷积、池化
文章目录
- 卷积、池化
- 一、卷积
-
- 1.定义:
- 2.目的
- 3.卷积核
-
- 卷积核的作用:
- 卷积核一般为奇数
- 卷积核示例:
- 4.步长stride
- 5.padding
- 6.公式
- 7.卷积核的选择@@@
- 二、池化
-
- 1定义:
- 2.目的
- 3.分类:
- 4.公式
一、卷积
1.定义:
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n),则卷积的结果
-
中文名
卷积
-
外文名
Convolution
-
定 义
分析数学中一种重要的运算
-
其 他
可以被看作是“滑动平均”的推广
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YWuRWjz3-1573636622609)(C:\Users\WMY\Pictures\Saved Pictures\卷积\2018080411520076.gif)]
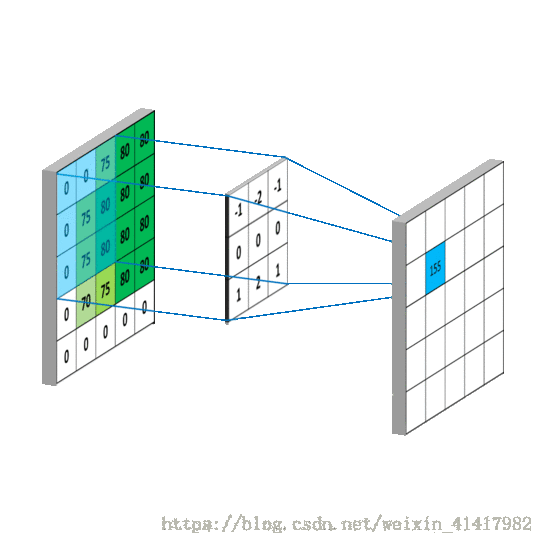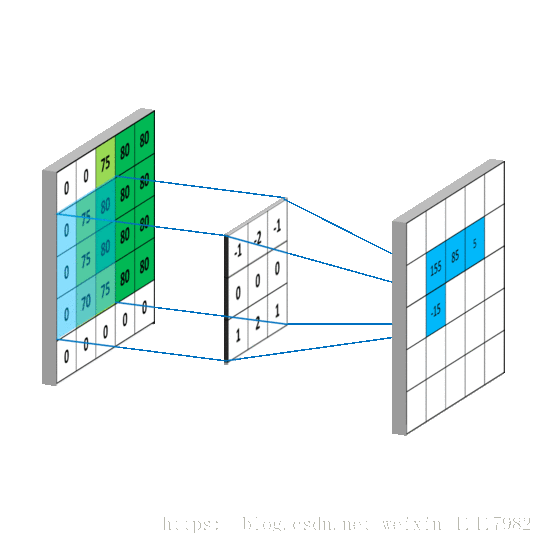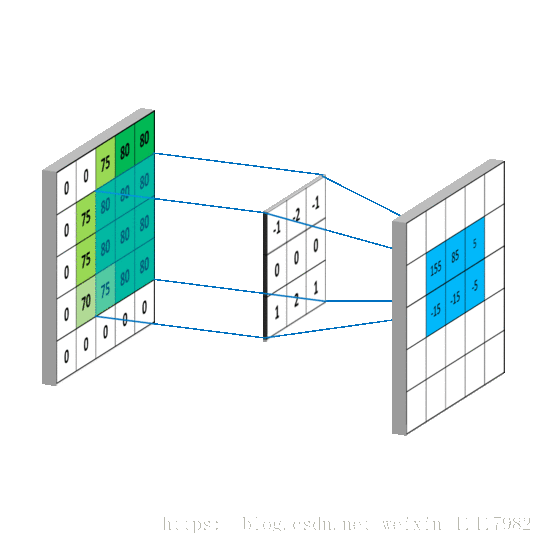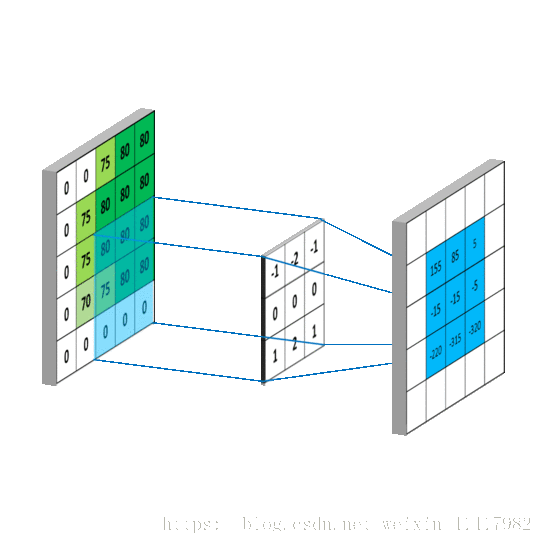
2.目的
深层神经网络中使用卷积的优点:参数共享,稀疏连接
【1】参数共享(Parameter Sharing)
准确的定义如下:
A feature detector (such as a vertical edge detector) that’s useful in one part of the image is probably useful in another part of the image.
直观的理解就是,一个卷积核,如果它适用于一幅图片的左上角做边缘检测,则他也能适用于图片的右下角。
卷积核的参数不需要改动,就能被适应,这就是所谓参数共享。
【2】稀疏连接(Sparsity of Connections)
准确的定义如下:
In each layer, each output value depends only on a small number of inputs.
直观的理解就是,卷积输出的每一个数值(像素),只与卷积核大小的像素值有关,与卷积核范围之外的其它像素无关。
结论
深层神经网络中使用卷积,可以通过参数共享和稀疏连接,减少参数。参数少了,我们就能用更少的训练集来训练网络,从而预防过拟合。
卷积层只需要很少的参数,就能连接两个很大维度的特征
全连接层,要连接两个很大维度的特征,参数会非常多
3.卷积核
卷积核的作用:
滤波**/**特征提取**
假设有一个卷积核如下图所示:
![]()
我们可以看到小鼠各部分和它做卷积的结果。图形越相似,所得结果也就越大。
![]()
![]()
![]() .
.
卷积核一般为奇数
卷积核一般都把size设为奇数,主要有以下两个原因:
【1】保证了锚点(卷积核的中心)刚好在中间,方便以模块中心为标准进行滑动卷积。
【2】保证了padding时,图像的两边依然相对称。
1、奇数卷积核有中心像素点
如下图中,奇数大小的卷积核有唯一的中心像素点,而偶数大小的卷积核没有中心像素点
为什么需要中心像素点?因为中心像素点有以下两点左右:
确定局部卷积后要更新的像素点位置。如下图的卷积操作,中心像素的位置对应着当前卷积操作wx+b的值要赋给那个位置。如果卷积核是偶数,中心位置有四个像素。一种可能的解决方式是同时更新这四个像素的值,但这样会增加计算量。同时以步长stride=1移动卷积核时,会覆盖之前的值,造成计算浪费。
便于进行卷积操作,以中心点移动卷积核,(这点好像有点牵强,以左上角或右下角任一点像素也可移动卷积核)
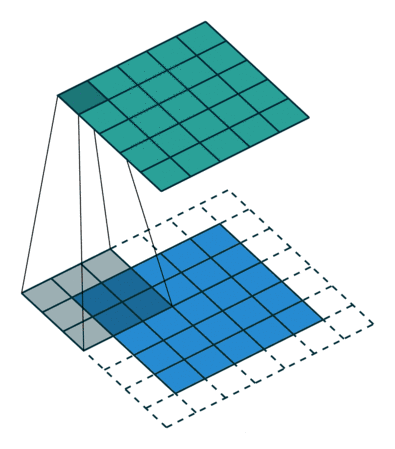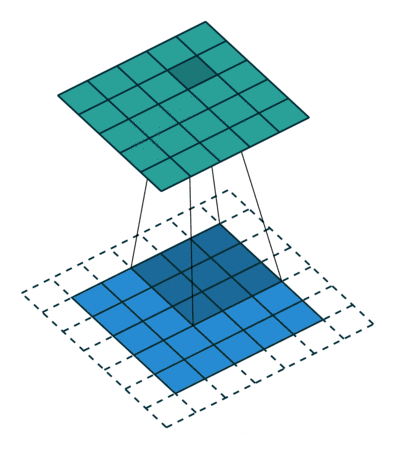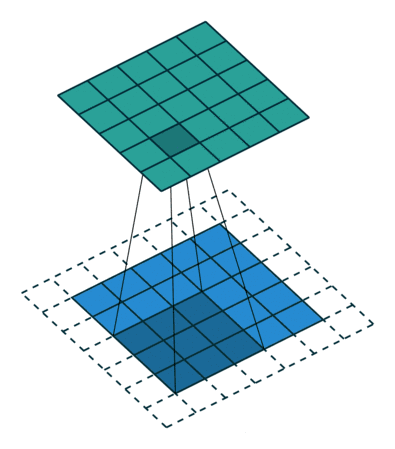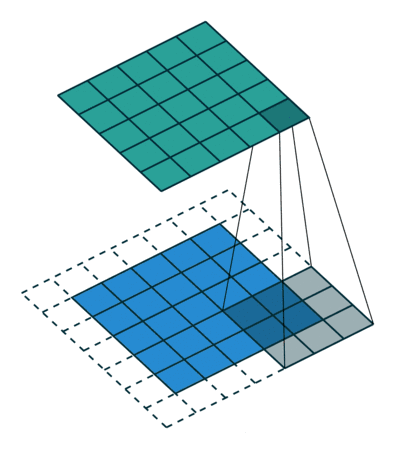
2、奇数的卷积核便于图像进行对称的补0padding
卷积有好几种方式如valid,same。其中same卷积的方式如上面卷积示例图所示,是为了保持卷积后特征图大小不变,在卷积操作进行前先在图像的周围补0。假设卷积前特征图大小为m,卷积核大小为k,那么正常情况下卷积后特征图大小n应该为m-k+1。既
为了使卷积后特征图大小保持不变,在卷积前把特征图的尺寸增大k-1。然后在进行卷积操作。此时
也就是卷积操作前后特征图大小相等。
为了使特征图增大k-1。通常使用的方式是在图像周围补0。如果卷积核的大小是奇数,则k-1为偶数。则可以在图像两侧进行对称的padding。左右上下各补充(k-1)/2。
更多细节见 https://blog.csdn.net/MrR1ght/article/details/99472017
卷积核示例:
Sobel卷积核(Gx表示水平方向,Gy表示垂直方向)
![]()
![]()
卷积后
![]()
![]()
4.步长stride
控制卷积核移动的距离
步长stride是一个一维的向量,长度为4。形式是[a,x,y,z],分别代表[batch滑动步长,水平滑动步长,垂直滑动步长,通道滑动步长]
在tensorflow中,stride的一般形式是[1,x,y,1]
第一个1表示:在batch维度上的滑动步长为1,即不跳过任何一个样本
x表示:卷积核的水平滑动步长
y表示:卷积核的垂直滑动步长
最后一个1表示:在通道维度上的滑动步长为1,即不跳过任何一个颜色通道
原文链接:https://blog.csdn.net/u014453898/article/details/81517975
5.padding
卷积操作存在两个问题:
1、图像越来越小;
2、图像边界信息丢失,即有些图像角落和边界的信息发挥作用较少。
因此需要padding
一张M x M的图片,经过卷积核F x F,strides = [1,1,1,1], padding = valid 卷积操作后,
得到大小为 C_side x C_side 的 feature map,
其中,
C_side = M - ( F - 1 ), 即边长减少了 F-1个单位
若想保持卷积后的图像大小不变,需要在原图边长基础上padding F-1个单位的零元素,
即经过 strides = [1,1,1,1], padding = same 卷积操作后,
C_side = ( M +2P )- ( F - 1 ) = M
P = ( F - 1 )/ 2
一般的,卷积核边长大小F为奇数:
1、方便padding = same卷积操作,左右(上下)两边对称补零;
2、奇数卷积核有中心像素,便于确定卷积核的位置。
当卷积步长strides不为1时,边长计算公式如下:
For the SAME padding, the output height and width are computed as:
out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2])) And
For the VALID padding, the output height and width are computed as:
out_height = ceil(float(in_height - filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width - filter_width + 1) / float(strides[2]))
原文链接:https://blog.csdn.net/zhaozx19950803/article/details/80409502
6.公式
原文链接: :https://blog.csdn.net/weixin_36836622/article/details/90473315
7.卷积核的选择@@@
如何选择卷积核的大小?越大越好还是越小越好?
答案是小而深,单独较小的卷积核也是不好的,只有堆叠很多小的卷积核,模型的性能才会提升。
CNN的卷积核对应一个感受野,这使得每一个神经元不需要对全局图像做感受,每个神经元只感受局部的图像区域,然后在更高层,将这些感受不同局部的神经元综合起来就可以得到全局信息。这样做的一个好处就是可以减少大量训练的参数。
VGG经常出现多个完全一样的3×3的卷积核堆叠在一起的情况,这些多个小型卷积核堆叠的设计其实是非常有效的。两个3×3的卷积层串联相当于1个5×5的卷积层,即一个像素会和周围5×5的像素产生关联,可以说感受野是5×5。同时,3个串联的3×3卷积层串联的效果相当于一个7×7的卷积层。除此之外,3个串联的3×3的卷积层拥有比一个7×7更少的参数量,只有后者的 (3×3×3) / (7×7) = 55%。最重要的是3个3×3的卷积层拥有比一个7×7的卷积层更多的非线性变换(前者可以使用三次ReLu激活,而后者只有一次)。
三个3x3感受野的叠加效果等同于一个7x7的感受野,为什么用三个3x3而不用一个7x7?
(1)使用三个非线性修正函数,使得决策函数更可分。
(2)减少了参数数量;
2.为什么使用1x1卷积核?
在不影响卷积层的感受野前提下,增加了决策函数的非线性性。
原文链接:https://blog.csdn.net/shayashi/article/details/86506347
原文链接:https://blog.csdn.net/fu6543210/article/details/82817916
二、池化
1定义:
对图像的某一个区域用某一个值代替
池化(Pooling):也称为欠采样或下采样。
2.目的
(1)下采样(downsamping)
(2)减少参数量
降维、去除冗余信息、对特征进行压缩、简化网络复杂度、减小计算量、减小内存消耗等等
(3)实现非线性
(4)可以扩大感知野。
(5)可以实现不变性,其中不变形性包括,平移不变性、旋转不变性和尺度不变性。
原文链接:https://blog.csdn.net/XX_123_1_RJ/article/details/86677482。
3.分类:
-
-
Max Pooling:最大池化
-
Average Pooling:平均池化
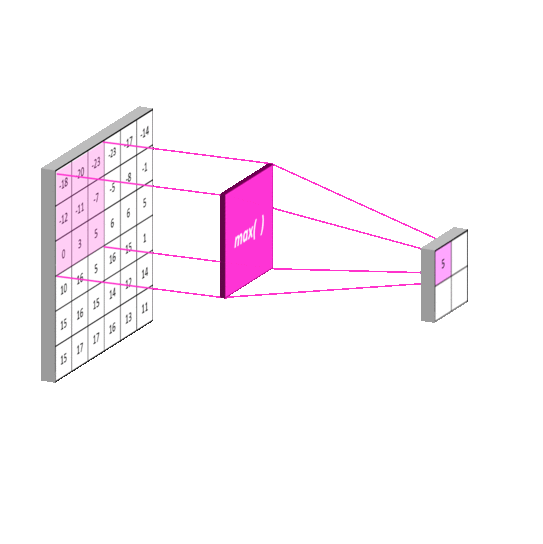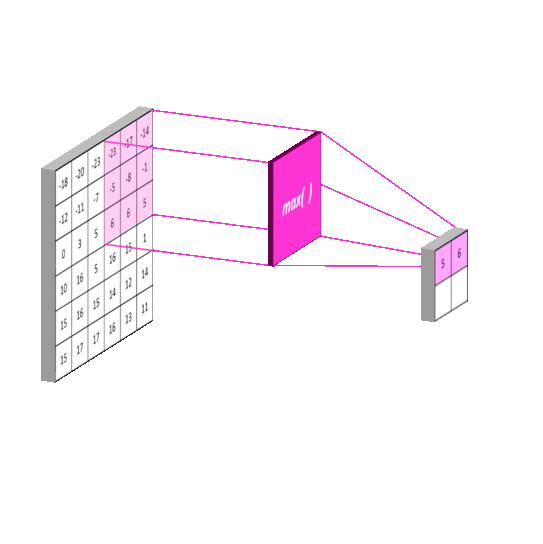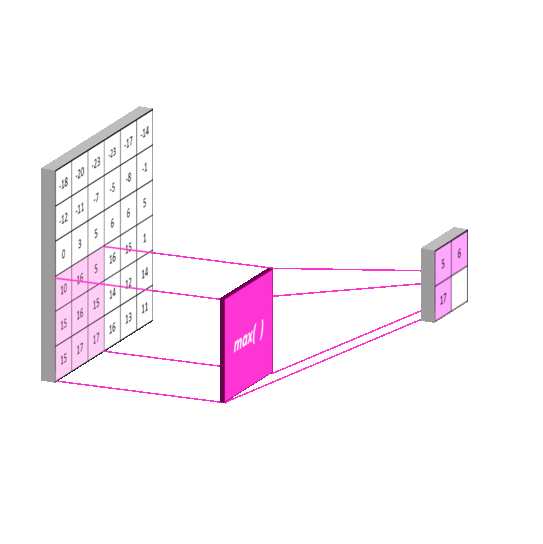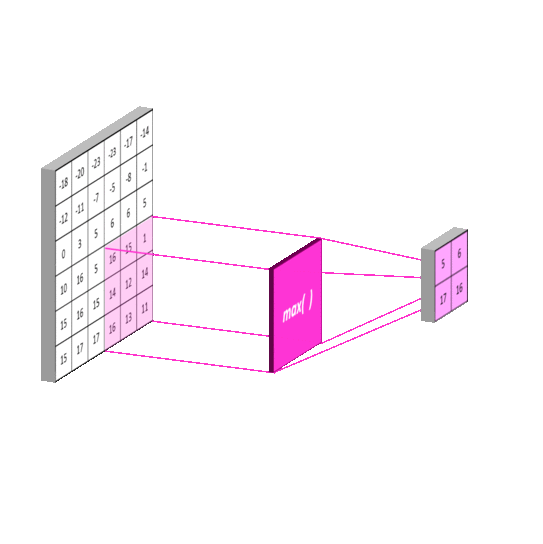
-
mean-pooling能减小邻域大小受限造成的估计值方差增大,更多的保留图像的背景信息,
max-pooling能减小 卷积层参数误差造成估计均值的偏移,更多的保留纹理信息。
Stochastic-pooling则介于两者之间,通过对像素点按照数值大小赋予概率,再按照概率进行亚采样,在平均意义上,与mean-pooling近似,在局部意义上,则服从max-pooling的准则
4.公式
@@@人在认识图像时,理解顺序为
图片的颜色、亮度—— 边缘、角点、直线(局部特征)——纹理、几何形状
计算机识别图像,假设是个猫的耳朵
训练时,卷积——池化——全连接——线性变换——激活函数——输出特征向量n1(计算机就认为这个特征向量是猫耳朵)
ss=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl8zNjgzNjYyMg==,size_16,color_FFFFFF,t_70)
@@@人在认识图像时,理解顺序为
图片的颜色、亮度—— 边缘、角点、直线(局部特征)——纹理、几何形状
计算机识别图像,假设是个猫的耳朵
训练时,卷积——池化——全连接——线性变换——激活函数——输出特征向量n1(计算机就认为这个特征向量是猫耳朵)
测试时,由输入图片得到的特征向量n2,计算机就对一下答案,看它俩是不是一样 maybe是这样