专题一 MATLAB基础知识
此部分为慕课，中南大学科学计算与MATLAB语言课程所做笔记。
文章目录
- 专题一 MATLAB基础知识
-
- 1.1 MATLAB系统环境
- 1.2 MATLAB数值数据
-
- 数值数据类型的分类
- 数值数据输出格式
- 常用数学函数
- 1.3 变量及其操作
-
- 变量与赋值语句
- 预定义变量
- 变量的管理
- 1.4 MATLAB矩阵的表示
-
- 矩阵的建立
- 冒号表达式
- 结构矩阵和单元
- 1.5 矩阵元素的引用
-
- 矩阵元素的引用方式
- 利用冒号表达式获得子矩阵
- 利用空矩阵删除矩阵的元素
- 改变矩阵的形状
- 1.6 MATLAB基本运算
-
- 算术运算
- 逻辑运算
- 1.7 字符串处理
-
- 字符串的表示
- 字符串的操作
专题一 MATLAB基础知识
1.1 MATLAB系统环境
设置当前文件夹窗口：
cd e:\matlab_work
Matlab的搜索路径：
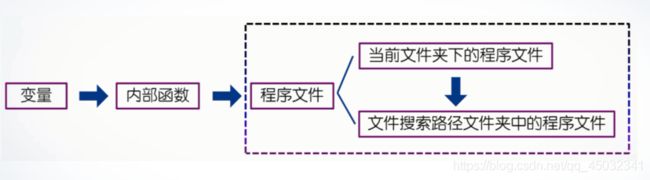用 path 命令设置 文件 搜索路径 ：
path(path,‘e:\matlab_work’)
1.2 MATLAB数值数据
数值数据类型的分类
- 整型
- 浮点型
- 复数型
（1）整型：
无符号整数：无符号8位整数、无符号16位整数、无符号32位整数、无符号64位整数。
带符号整数：带符号8位整数、带符号16位整数、带符号32位整数、带符号64位。
int8()
uint8()
（2）浮点型
single函数：将其他类型的数据转换为单精度型。
double函数：将其他类型的数据转换为双精度型 。
class(4)：返回数据类型。
（3）复数型
复型数据包括实部和虚部两个部分，实部和虚部默认为双精度型，虚数单位用i或j来表示。
real 函数 ：求复数的实部。
imag 函数：求复数的虚部。
>> 1+2i
ans =
1.0000 + 2.0000i
>> 1+2j
ans =
1.0000 + 2.0000i
数值数据输出格式
format命令的格式：format 格式符
>> foamat long
>> 50/3
ans =
16.6666666666666668
>> format
>> 50/3
ans =
16.6667
注意：format 命令只影响数据输出格式，而不影响数据的计算和存储 。
常用数学函数
- exp()：以e为底指数形式
- sin()、sind()：三角函数有以弧度为单位的函数和以角度为单位的函数，如果是以角度为单位的函数，就在函数名后面加“d”
- abs()：以求实数的绝对值、复数的模、字符串的 ASCII 码值
- fix()、 floor() 、ceil()、 round()：用于取整，round 函数是按照四舍五入的规则来取整；ceil是向上取整，取大于等于这个数的第一个整数；floor是向下取整，取小于等于这个数的第一个整数；fix是固定取靠近0的那个整数，也就是舍去小数取整
- rem()：例如，rem(m,10)，m除以10，取余数
- isprime()：返回是素数的元素
- find()：返回索引号
求[0,100]所有素数：
>> x = 0:100;
>> k = isprime(x);
>> k1 = find(k);
>> p = x(k1)
1.3 变量及其操作
变量与赋值语句
在MATLAB中，变量名是以字母开头，后接字母、数字或下画线的字符序列，最多 63个字符。
预定义变量
预定义变量是在MATLAB工作空间中驻留，由系统本身定义的变量 。
- ans是默认赋值变量
- i和j代表虚数单位
- pi代表圆周率
- NaN代表非数字
变量的管理
（1）who和whos
who：返回变量名
whos：返回变量名及其信息
（2）内存变量文件
用于保存MATLAB工作区变量的文件叫做内存变量文件，其扩展名为.mat，也叫 MAT 文件 。
- save命令：创造内存变量文件
- load文件：装入内存变量文件
>> save mydata k k1;
>> load mydata
1.4 MATLAB矩阵的表示
矩阵的建立
（1） 利用直接输入法建立矩阵: : 将矩阵的元素用中括号括起来，按矩阵行的顺序输入各元素，同一行的各元素之间用 逗号或空格分隔，不同行的元素之间用分号分隔。
（2）利用已建好的矩阵建立更大的矩阵，一个大矩阵可以由已经建立好的小矩阵拼接而成。
>> A = [1,2,3;4,5,6;7,8,9];
>> B = [-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C = [A,B;B,A]
（3）用实部矩阵和虚部矩阵构成复数矩阵
>> A = [1,2,3;4,5,6;7,8,9];
>> B = [-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C = A + B*i
冒号表达式
（1）格式：初始值：步长：中止值
（2）linspace(a,b,n)：[a,b]之间产生n个数。
注意：当n省略时，自动产生100个元素
结构矩阵和单元
（1） 结构矩阵
由结构数据构成的矩阵就是结构矩阵，结构矩阵里的每个元素就是结构数据类型。
格式为：
结构矩阵元素.成员名=表达式
>>a(1).x1=10;
>>a(1).x2='sang';
>>a(1).x3=[1,2;3,4];
（2）单元矩阵
建立单元矩阵和一般矩阵相似，直接输入就可以了，只是单元矩阵元素用大括号括起来。
a = {10,'sang', [1,2,;3,4];11, 'tian', [9,9;7,8]};
1.5 矩阵元素的引用
矩阵元素的引用方式
（1）通过下标来引用 矩阵的元素
A(3,2)表示A矩阵第3行第2列的元素
>> A(3,2) = 10
注意：如果给出的行下标或列下标大于原来矩阵的行数和列数，那么 MATLAB 将自动扩展原来的矩阵，并将扩展后没有赋值的矩阵元素置为0。
>> A = [1,2,3;4,5,6];
>> A(4,5) = 10
A =
1 2 3 0 0
4 5 6 0 0
0 0 0 0 0
0 0 0 0 10
（2）通过下标来引用 矩阵的元素
在 MATLAB 中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，一直到矩阵的最后一列元素。
矩阵元素的序号就是矩阵元素在内存中的排列顺序。
>> A = [1,2,3;4,5,6];
>> A(3)
ans =
2
序号与下标是一一对应的，以m*n矩阵A为例,矩阵元素 A(i,j)的序号为 (j-1) *m+i。
- sub2ind函数：将矩阵中指定元素的行、列下标转换成存储的序号 。通用格式：D=sub2ind(S,I,J)，D，序号；S，行数和列数组成的向量；I，转换矩阵的行下表；J，转换矩阵的列下表。
- ind2sub函数 ：将把矩阵元素的序号转换成对应的下标 ，其调用格式为：[I,J] = ind2sub(S,D)，I，行下标；J，列下标；S，行数和列数组成的向量；D，序号。
sub2ind函数举例：
>> clear
>> A = [1:3;4:6];
>> A
A =
1 2 3
4 5 6
>> D = sub2ind(size(A),[1,2;2,2],[1,1;3,2])
D =
1 2
6 4
ind2sub函数举例：
>> [I,J] = ind2sub([3,3],[1,3,5])
I =
1 3 2
J =
1 1 2
利用冒号表达式获得子矩阵
子矩阵是指由矩阵中的一部分元素构成的矩阵
- A(i,:)：第i行的全部元素
- A(:,j)：第j列的全部元素
end 运算符：表示某一维的末尾元素下标。
利用空矩阵删除矩阵的元素
空矩阵是指没有任何元素的矩阵。
>> clear
>> A = [1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]
A =
1 2 3 0 0
7 0 9 2 6
1 4 -1 1 8
>> A(:,[2,4]) = []
A =
1 3 0
7 9 6
1 -1 8
改变矩阵的形状
reshape( A,m,n)：在矩阵总元素保持不变的前提下，将矩阵A重新排成m m ×n n 的二维矩阵。
注意： reshape 函数只是改变原矩阵的行数和列数，但并不改变原矩阵元素个数及其存储顺序。
>> clear
>> A = [1,2,3,4,5,6,7,8,9];
>>> B = reshape(A,3,3)
B =
1 4 7
2 5 8
3 6 9
1.6 MATLAB基本运算
算术运算
（1）基本算术运算
基本算术运算符：＋(加) 、－(减) 、*(乘) 、 /( 右除) ) 、(左除) 、^(乘方) 。
- MATLAB的算术运算是在矩阵意义下进行的。
- 单个数据的算术运算只是矩阵运算的一种特例。
注意：MATLAB的运算是在矩阵意义下进行的，单个数据的算术运算只是矩阵运算的一种特例。
加减运算
- 若两矩阵同型，则运算时两矩阵的相应元素相加减。
- 若两矩阵不同型，则MATLAB将给出错误信息。
- 一个标量也可以和矩阵进行加减运算，这时把标量和矩阵的每一个元素进行加减运算。
乘法运算
- 矩阵A和B进行乘法运算，要求A的列数与B的行数相等，此时则称A、B矩阵是可乘的，或称A和B两矩阵维数和大小相容。
- 如果两者的维数或大小不相容，则将给出错误信息，提示用户两个矩阵是不可乘的。
除法运算
在MATLAB中，有两种矩阵除法运算：右除/和左除\ 。如果A矩阵是非奇异方阵，则B/A等效于B*inv (A) ，A\B等效于inv(A)*B 。
>> clear
>> A = [1,2,3;4,2,6;7,4,9];
>> B = [4,3,2;7,5,1;12,7,92];
>> C1 = B/A
C1 =
-0.1667 -3.3333 2.5000
-0.8333 -7.6667 5.5000
12.8333 63.6667 -36.5000
乘方运算
一个矩阵的乘方运算可以表示成A^x，要求A为方阵，x为标量。
>> clear
>> A=[1,2,3;4,5,6;7,8,0];
>> A^2
ans =
30 36 15
66 81 42
39 54 69
（2）点运算
- 点运算符：.*和./和.\和.^。
- 两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵同型。
>> clear
>> A = [1,2,3;4,5,6;7,8,9];
>> B = [-1,0,1;1,-1,0;0,1,1];
>> C = A.*B
C =
-1 0 3
4 -5 0
0 8 9
>> D = A*B
D =
1 1 4
1 1 10
1 1 16
例如：当x=0.1、0.4、0.7、1时，分别求y=sin(x) * cos(x)的值。
>> clear
>> x = 0.1:0.3:1;
>> y = sin(x).*cos(x)
y =
0.0993 0.3587 0.4927 0.4546```
### 关系运算
- 关系运算符： <( 小于)、<=(小于或等于) 、>(大于) 、>=(大于或等于) 、==(等于) 、～=(不等于) 。
- 当两个比较量是标量时，直接比较两数的大小。若关系成立，关系表达式结果为1，否则为0 。
- 当参与比较的量是两个同型的矩阵时，比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行，最终的关系运算的结果是一个与原矩阵同型的矩阵 ，它的元素由0或1组成。
- 当参与比较的一个是标量，而另一个是矩阵时，则把标量与矩阵的每一个元素按标量关系运算规则逐个比较，最终的关系运算的结果是一个与原矩阵同型的矩阵，它的元素由0或1组成。
例：建立3阶方阵A，判断A的元素是否为偶数。
```markup
>> clear
>> A = [24,35,13;22,63,23;39,47,80];
>> A
A =
24 35 13
22 63 23
39 47 80
>> P = rem(A,2)
P =
0 1 1
0 1 1
1 1 0
逻辑运算
逻辑运算符： &(与) 、 |(或) 和～(非)
设参与逻辑运算的是两个标量a和b，那么运算规则为：
- a&b a、b全为非零时，运算结果为1，否则为0。
- a|b a、b中只要有一个为非零时，运算结果为1 。
- ~a当a为零时，运算结果为1；当a为非零时，运算结果为0。
例如：水仙花数是指各位数字的立方之和等于该数本身的三位正整数，求全部水仙花数。
>> clear
>> x = 100:999;
>> x1 = rem(x,10);
>> x2 = rem(fix(x/10),10);
>> x3 = fix(x/100);
>> k = find((x1.^3+x2.^3+x3.^3 == x));
>> s = x(k)
1.7 字符串处理
字符串的表示
（1）在MATLAB中,字符串是用单引号括起来的字符序列:
>> clear
>> name = 'My name is sang';
>> a = name(1:2)
a =
'My'
（2）若字符串中的字符含有单引号，则该单引号字符要用两个单引号来表示:
>> clear
>> name = 'I''m sang!'
name =
'I'm sang!'
（3）建立多行字符串，形成字符串矩阵
>> clear
>> x = ['abcde';'12345'];
>> x
x =
2×5 char 数组
'abcde'
'12345'
>> x(2,5)
ans =
'5'
length()：计算长度。
字符串的操作
（1）字符串的执行
格式： eval(s) s为字符串
>> clear
>> t = pi;
>> m = '[t,sin(t),cos(t)]';
>> y = eval(m)
y =
3.1416 0.0000 -1.0000
（2）字符串之间的转换
- abs 和 double 函数都可以用来获取字符串矩阵所对应的 ASCII 码数值矩阵。
- char 函数可以把 ASCII 码矩阵转换为字符串矩阵。
>> clear
>> s1 = 'MATLAB';
>> a = abs(s1)
a =
77 65 84 76 65 66
>> char(s1+32)
ans =
'matlab'
（3）字符串的比较
字符串的比较有两种方法：利用关系运算符或字符串比较函数。
- strcmp (s1,s2) ： 用来比较字符串 s1 和 s2 是否相等，如果相等，返回结果为 1 ，否则返回 0 。
- strncmp (s1,s2,n) ： 用来比较两个字符串前 n 个字符是否相等，如果相等，返回 1 ，否则返回 0 。
- strcmpi (s1,s2) ： 在忽略字母大小写前提下，比较字符串 s1 和 s2 是否相等，如果相等，返回 1 ，否则返回 0 。
- strncmpi (s1,s2,n) ： 在忽略字符串大小写前提下，比较两个字符串前 n 个字符是否相等，如果相等，返回 1 ，否则返回 0 。
>> clear
>> strcmp('www0','w123')
ans =
logical
0
>> strncmpi('www0','W123',1)
ans =
logical
1
（3）字符串的 查找与替换
- findstr (s1,s2) ：返回短字符串在长字符串中的开始位置。
- strrep (s1,s2,s3) ：将字符串 s1 中的所有子字符串 s2 替换为字符串 s3。