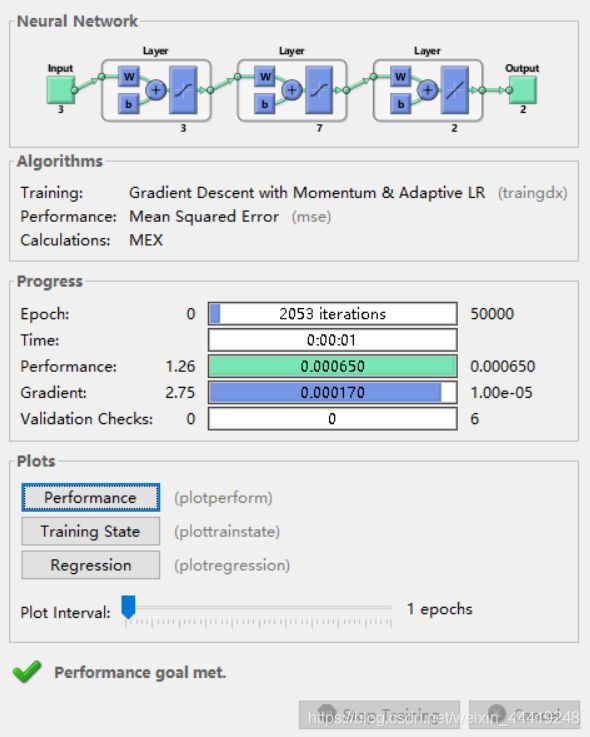
神经网络预测函数的根
假设已知X1={X1,X2,X3...},X2={X,1X2,X3...},X3={X1,X2,X3...},Y1={Y1,Y2,Y3...},Y2={Y11,Y22,Y33...}
测量数据Y{x1,X11;x2,X22;x3,X33;}
其中,Y1与X1~X3有关,Y2也与X1~X3有关,
p=[X1;X2;X3]; %输入数据矩阵
t=[Y1;Y2]; %目标数据矩阵%利用premnmx函数对数据进行归一化
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%BP网络训练
net=newff(dx,[3,7,2],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000; %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=50000; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3); %均方误差
net=train(net,pn,tn); %开始训练,其中pn,tn分别为输入输出样本
%利用原始数据对BP网络仿真
an=sim(net,pn); %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt); % 把仿真得到的数据还原为原始的数量级;
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1990:2009;
newk=a(1,:);
newh=a(2,:);
figure (2);
subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+')
legend('网络输出客运量','实际客运量');
xlabel('年份');ylabel('客运量/万人');
subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+')
legend('网络输出货运量','实际货运量');
xlabel('年份');ylabel('货运量/万吨');
%利用训练好的网络进行预测
% 当用训练好的网络对新数据pnew进行预测时,也应作相应的处理:
pnew=[X1 X11
X2 X2
X3 X33];
pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;
anewn=sim(net,pnewn); %利用归一化后的数据进行仿真;
anew=postmnmx(anewn,mint,maxt) %把仿真得到的数据还原为原始的数量级;