《视觉SLAM十四讲》学习笔记：第5讲相机与图像

《视觉SLAM十四讲》学习笔记：第5讲相机与图像

前言：本学习笔记将记录《视觉SLAM十四将》中一些重要的知识点，并对书中一些比较难的知识点添加上一些笔者个人的理解，以供笔者本人复习并与各位同学一起交流学习。本笔记结构将与原书结构一致，如果某一目录下面没有任何笔记，则代表笔者认为该小节内容相对来说没有过多重点知识。

本讲主要解决问题
本讲只要讨论机器人如何观测外部世界，也就是观测方程部分。
理论：
1.理解针孔相机的模型、内参与径向畸变参数。
2.理解一个空间点是如何投影到相机成像平面的。
实践：
3.掌握OpenCV的图像存储与表达方式。
4.学会基本的摄像头标定方法。

5.1 相机模型

5.1.1 针孔相机模型
针孔相机模型，也就是简单的小孔成像模型，如下图所示：

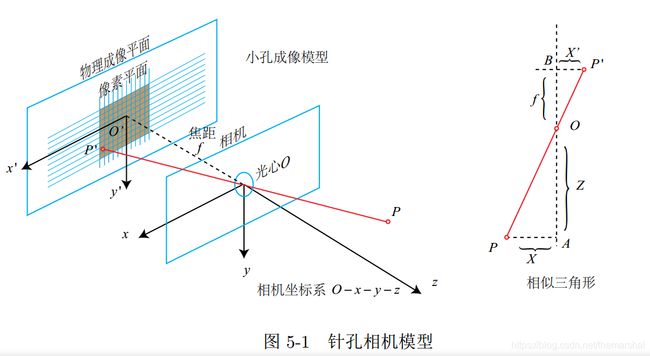
现在来对这个简单的针孔模型进行几何建模。设$O-x-y-z$为相机坐标系，习惯上我们让$z$轴指向相机前方，$x$向右，$y$向下。$O$为摄像机的广信，也是针孔模型中的针孔。现实世界的空间点$P$，经过小孔$O$投影之后，落在物理成像平面$O^{\prime }-x^{\prime }-y^{\prime }$上，成像点为$P^{\prime }$。设P的坐标为$[X,Y,Z{]}^T$，$P^{\prime }$为$[X^{\prime },Y^{\prime },Z^{\prime }{]}^T$，并且设物理成像平面到小孔的距离为$f$（焦距）。那么，根据三角形相似关系，有：

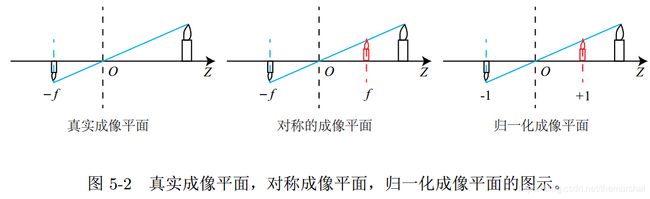
其中负号表示成的像是倒立的。为了简化模型，我们把可以成像平面对称到相机前面，和三维空间点一起放在摄像机坐标系的同一侧（注意，后面的对称平面和归一化平面其实都是虚拟的平面），这样可以把公式中的负号去掉：

真实的成像平面，对称的成像平面和归一化成像平面如下图所示：

整理得：

虽然式(5.3)描述了点$P$和它的像之间的空间关系。不过，在相机中，我们最终获得的是一个个的像素，这需要在成像平面上对像进行采样和量化。为了描述传感器将感受到的光线转换成图像像素的过程，我们设在物理成像平面上固定着一个像素平面$o-u-v$。我们在像素平面得到了$P^{\prime }$的像素坐标：$[u,v{]}^T$。
像素坐标系通常的定义方式是：原点$o^{\prime }$位于图像的左上角，$u$轴向右与$x$轴平行，$v$轴向下与$y$轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。我们设像素坐标在$u$轴上缩放了$\alpha$倍，在$v$上缩放了$\beta$倍。同时，原点平移了$[c_x,c_y{]}^T$。那么，$P^{\prime }$的坐标与像素坐标$[u,v{]}^T$的关系为：

代入式（5.3）并把$\alpha f$合并成$f_x$，把$\beta f$合并成$f_y$,得：

关注单位：$f$的单位为米，$\alpha ,\beta$的单位为像素每米，所以$f_x,f_y$的单位为像素。把该式写成矩阵形式，会更加简洁，不过左侧需要用到齐次坐标：

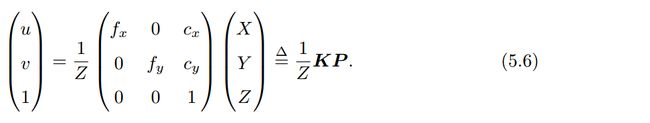
按照习惯，将$Z$挪到左侧：

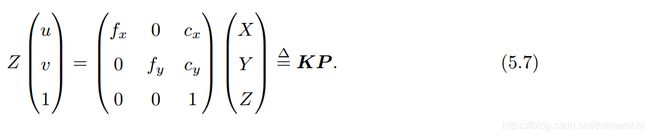
该式中，我们把中间的量组成的矩阵称为相机的内参数矩阵$K$。通常认为，相机的内参在出厂之后是固定的，不会在使用过程中发生变换。有的相机生产厂商会告诉你相机的内参，而有时需要自己确定相机的内参，也就是标定。
除了内参之外，相机还有相对的外参。在式（5.6）中，我们使用的是$P$在相机坐标系下的。由于相机在运动，所以$P$的相机坐标应该是它的世界坐标(记为$P_w$)，根据相机的当前位姿，变换到相机坐标系下的结果。（即$P$的坐标是相机坐标系下）。相机的位姿由它的旋转矩阵$R$和平移向量$t$来描述，那么有：

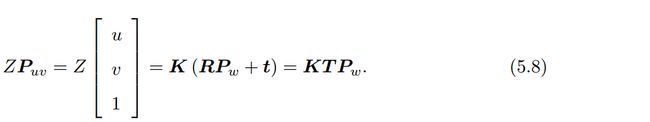
这里第三个等号左右两边利用了齐次坐标的转换。这个齐次坐标的转换描述里$P$的世界坐标到像素坐标的投影关系。其中，相机的位姿$R,t$又称为相机的外参数。相比于不变的内参，外参会随着相机运动发生改变，用是也是$SLAM$中待估计的目标，代表着机器人的轨迹。
上式两侧都是齐次坐标。因为齐次坐标乘上非零常数后表达同样的含义，所以可以简单地把$Z$去掉：

但这样等号意义就变里，成为在齐次坐标下像等的概念，相差里一个非零常数。
这里作者重点提了一下齐次到非齐次的变换。可以看到，右侧的$T{P}_W$表示把一个世界坐标系下的齐次坐标，变换到相机坐标系下。为了使它与$K$相乘，需要取它的前三维组成向量——因此$T{P}_w$最后一维为1。此时，对于这个三维向量，我们还可以按照齐次坐标的方式，把最后一维进行归一化处理，得到了$P$在相机归一化平面上的投影：

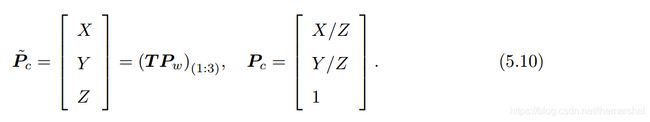
这时 $P_c$ 可以看成一个二维的齐次坐标，称为归一化坐标。它位于相机前方 $z=1$ 处的平面上。该平面称为归一化平面。由于 $P_c$ 经过内参之后就得到了像素坐标，所以我们可以把像素坐标 $[u,v{]}^T$，看成对归一化平面上的点进行量化测量的结果。
5.1.2 畸变
畸变是由透镜产生的，由透镜形状引起的畸变称为径向畸变，由透镜安装不与成像面严格平行产生的畸变为切向畸变。其中，径向畸变又分为桶形失真和枕形失真，如下图所示：

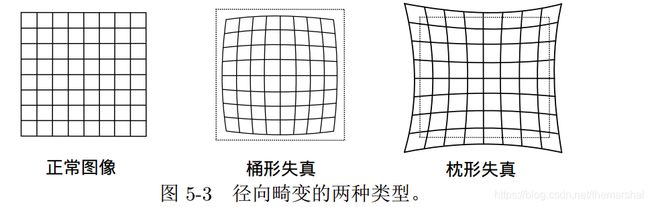
桶形畸变是由于图像放大率随着离光轴的距离增加而减小，而枕形畸变却恰好相反。在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。
利用数学方法来定义两种畸变就是，将平面上一点$p$用极坐标表示$[r,\theta {]}^T$，径向畸变可看成坐标点沿着长度方向发生里变化$\delta r$，也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生里变化，也就是水平夹角发生里变化$\delta \theta$。
因此，对于径向畸变，可以用和距中心距离有关的二次及高次多项式函数进行纠正：

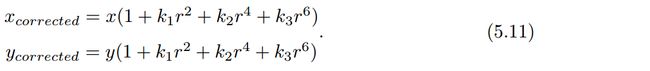
其中$[x,y{]}^T$是未纠正的点的坐标，$[x_{corrected},y_{corrected}{]}^T$是纠正后的点的坐标，注意它们都是归一化平面上的点，而不是像素平面上的点。在式（5.11）描述的纠正模型中，对于畸变较小的图像中心区域，畸变纠正主要是$k_1$起作用。而对于畸变较大的边缘区域主要是$k_2$起作用。普通摄像头用这两个系数就能很好的纠正径向畸变。对于畸变较大的摄像头，比如鱼眼镜头，可以加入$k_3$畸变项对畸变进行纠正，
而对于切向畸变，可以用另外两个参数$p1,p2$来进行纠正：

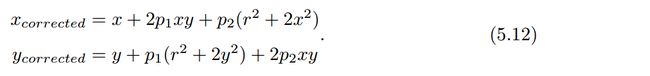
因此，联合式（5.11）和式（5.12），对于相机坐标系中的一点$P(X,Y,Z)$，我们能够通过五个畸变系数找到这个点在像素平面上的正确位置：
1.将三维空间点投影到归一化图像平面。设它的归一化坐标为$[x,y{]}^T$。
2.对归一化平面上的点进行径向畸变和切向畸变纠正。

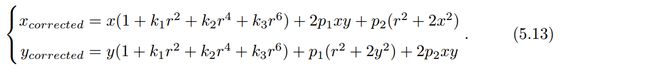
3.将纠正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置。

在上面的纠正畸变的过程中，我们使用里五个畸变项。实际应用中，可以灵活选择纠正模型，比如只选择$k_1,p_1,p_2$这三项等。
（注：获得三项系数的方式可以利用对黑白棋盘进行标定，然后利用matlab库函数求得参数，此处不过多赘述）。
在$SLAM$中，常见的去畸变的做法就是先对整张图像进行去畸变，得到去畸变后的图像，然后讨论此图像上的点的空间位置。因此，当一个图像去畸变后，就可以直接用针孔模型建立投影关系，而不用考虑畸变了。
最终，总结一下单目相机的成像过程：
1.首先，世界坐标系下有一个固定的点$P$,世界坐标为$P_w$;
2.由于相机在运动，它的运动由$R,t$或变换矩阵$T\in SE(3)$描述。$P$的相机坐标为：$P_c=R{P}_w+t$。
3.此时的$P_c$仍然有$X,Y,Z$三个量，把它们投影到归一化平面$Z=1$上，得到$P$的归一化相机坐标：$P_c=[X/Z,Y/Z,1{]}^T$。
4.对坐标进行去畸变化处理。
5.最后，$P$的归一化坐标经过内参后，对应到它的像素坐标：$P_{uv}=K{P}_c$。
注意到$Z$可能小于1，说明该点位于归一化平面后面，它可能不会在相机平面上成像，实践当中要检查一次。
5.1.3 双目相机模型
针孔相机模型描述里单目相机的成像模型，然而，该模型忽略里深度信息，也就无法确定这个空间点的具体位置的。而只有当$P$的深度确定时，我们才能确切地指导它的空间位置。
测量目标深度的方法有很多，双目相机主要依靠基线去进行测量：

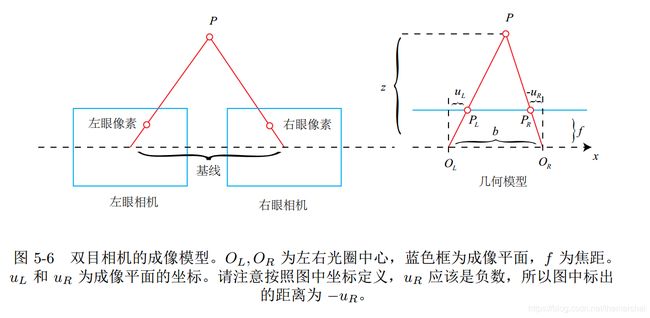
根据上图，同时，根据三角形相似关系，有：

稍作整理，得：

这里d为左右图的横坐标之差，称为视差。根据视差，可以估计一个像素离相机的距离。视差与距离成反比：视差越大，距离越近。同时，由于视差最小为一个像素，于是双目的深度存在一个理论上的最大值，由$fb$确定。我们看到，当基线越长时，双目最大能测到的距离就会变远；反之，小型双目器件则只能测量很近的距离。
虽然由视差计算深度的公式很简洁，但视差$d$本身的计算却比较困难。当我们想计算每个像素的深度时，其计算量与精度都将成为问题，而且只有在图像纹理变化丰富的地方才能计算视差。由于计算量的原因，双目深度估计仍需要使用$GPU或FPGA$来计算。
5.1.4 RGB-D相机模型
RGB-D相机可以主动测量每个像素的深度，原理主要有两大类：
1.通过红外结构光来测量像素距离的。
2.通过飞行时间法原理测量像素距离的。
无论是结构光还是 ToF， RGB-D 相机都需要向探测目标发射一束光线（通常是红外光）。在结构光原理中，相机根据返回的结构光图案，计算物体离自身的距离。而在 ToF中，相机向目标发射脉冲光，然后根据发送到返回之间的光束飞行时间，确定物体离自身的距离。 ToF 原理和激光传感器十分相似，不过激光是通过逐点扫描来获取距离，而 ToF相机则可以获得整个图像的像素深度，这也正是 RGB-D 相机的特点。所以，如果你把一个 RGB-D 相机拆开，通常会发现除了普通的摄像头之外，至少会有一个发射器和一个接收器。
在测量深度之后，RGB-D相机通常按照生产时的各个相机摆放位置，自己完成深度与彩色图像素之前的配对，输出一一对应的彩色图和深度图。我们可以在同一个图像位置，读取到色彩信息和距离信息，计算像素的3D相机坐标，生成点云。对RGB-D数据，既可以在图像层面进行处理，亦可在点云层面处理。
RGB-D相机能够实时地测量每个像素点的距离。但是，由于这种发射-接受的测量方式，使得它使用方面比较受限。用红外进行深度值测量的 RGB-D 相机，容易受到日光或其他传感器发射的红外光干扰，因此不能在室外使用，同时使用多个时也会相互干扰。对于透射材质的物体，因为接受不到反射光，所以无法测量这些点的位置。此外， RGB-D 相机在成本、功耗方面，都有一些劣势。

5.2 图像

本节的知识较为基础，但是此处不过多描述，但请注意分辨率的宽高与二维数组中的行列的对应关系。

5.3 实践：图像的存取与访问

这里有两点注意：
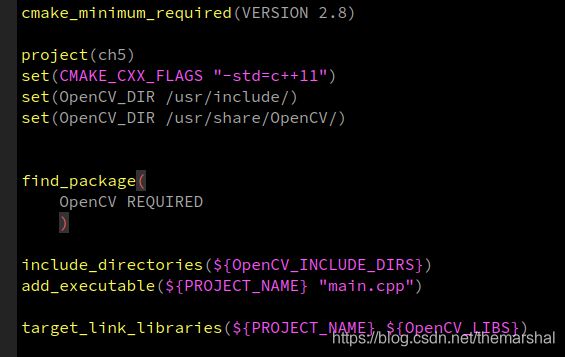
1.安装ros全家桶的时候就会帮你安装好OpenCV，不需要单独编译，个人安装的ros-melodic版本，cmakelist编辑如下，仅供参考：

2.注意区别赋值和clone的区别。

5.4 实践：拼接点云

拼接点云这边遇到的坑较多，踩坑集锦见博客：https://blog.csdn.net/themarshal/article/details/107467114