人工智能-数学基础-线性代数与仿射变换
此篇文章需要一些线性代数、矩阵分块和Numpy的基础,在文中对这些基础不再赘述
一. 坐标变换
1.1 一个点变换到另一个点
存 在 坐 标 点 ( x 1 , x 2 ) 需 要 变 换 到 ( y 1 , y 2 ) , 可 以 进 行 如 下 计 算 : 存在坐标点(x_1,x_2)需要变换到(y_1,y_2) ,可以进行如下计算: 存在坐标点(x1,x2)需要变换到(y1,y2),可以进行如下计算:
{ y 1 = a 11 x 1 + a 12 x 2 y 2 = a 21 x 1 + a 22 x 2 \begin{cases} y_1=a_{11}x_1+a_{12}x_2 \\ y_2=a_{21}x_1+a_{22}x_2 & \end{cases} { y1=a11x1+a12x2y2=a21x1+a22x2
以上代数计算关系可以写为矩阵运算关系:
[ y 1 y 2 ] = [ a 11 a 12 a 21 a 22 ] ⋅ [ x 1 x 2 ] \begin{bmatrix} y_1 \\ y_2 \\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} [y1y2]=[a11a21a12a22]⋅[x1x2]
y → = A ⋅ x → \overrightarrow{y} = A \cdot \overrightarrow{x} y=A⋅x
分量计算为:
y i = ∑ j = 1 2 a i j x j y_i = \sum_{j=1}^2a_{ij}x_j yi=j=1∑2aijxj
此为矩阵的点乘(内积)
1.2 n个点进行坐标变化
假 设 有 N 个 点 X ∈ R N × 2 , 多 有 点 均 进 行 矩 阵 预 算 : 假设有N个点 X \in \R^{N \times 2} ,多有点均进行矩阵预算: 假设有N个点X∈RN×2,多有点均进行矩阵预算:
注意:此时每一行代表了一个点
[ y 11 y 12 y 21 y 22 y 31 y 32 ] = [ x 11 x 12 x 21 x 22 x 31 x 32 ] ⋅ [ a 11 a 12 a 21 a 22 ] \begin{bmatrix} y_{11} & y_{12} \\ y_{21} & y_{22} \\ y_{31} & y_{32} \\ \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \\ \end{bmatrix} \cdot \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix} ⎣⎡y11y21y31y12y22y32⎦⎤=⎣⎡x11x21x31x12x22x32⎦⎤⋅[a11a21a12a22]
Y = X ⋅ A Y = X \cdot A Y=X⋅A
分量的形式:
y n i = ∑ j = 1 2 x n j a j i y_{ni} = \sum_{j=1}^2x_{nj}a_{ji} yni=j=1∑2xnjaji
1.3 M维空间数据
对 于 M 维 数 据 , X 为 n 行 m 列 数 据 X ∈ R n × m , A 为 m 行 k 列 数 据 A ∈ R m × k 对于M维数据, X为n行m列数据X \in \R^{n \times m},A为 m行k列数据A \in \R^{m \times k} 对于M维数据,X为n行m列数据X∈Rn×m,A为m行k列数据A∈Rm×k
Y = X ⋅ A Y = X \cdot A Y=X⋅A
Y 为 n 行 k 列 数 据 Y ∈ R n × k Y为 n行k列数据 Y\in \R^{n \times k} Y为n行k列数据Y∈Rn×k
分量的形式:
y i j = ∑ k m x i k a k m y_{ij} = \sum_k^mx_{ik}a_{km} yij=k∑mxikakm
所 以 , 如 果 需 要 对 n 维 空 间 中 的 点 进 行 变 换 , 则 需 要 A 满 足 m 行 m 列 , A ∈ R m × m 所以,如果需要对n维空间中的点进行变换,则需要 A满足m行m列,A \in \R^{m \times m} 所以,如果需要对n维空间中的点进行变换,则需要A满足m行m列,A∈Rm×m
二. 矩阵的仿射变换
2.1 我们先模拟一些点数据:
"""
模拟点数据
"""
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend("TkAgg")
# 随机生成 1000 行, 2列的范围从 (0-1)的数据
points = np.random.random([1000, 2])
# 生成均匀的1000个 0到2的数字
random_num = np.linspace(0, 2, 1000)
# 将 line_x 重调为 1000行 1 列的矩阵
line_x = np.reshape(random_num, [1000, 1])
# 将 line_x进行列拼接. 得到 1000行两列的数据, 该数据类似于 斜率 0.5的直线
line = np.concatenate([line_x, line_x], axis=1)
# 将散点和线性数据进行 行拼接, 得到 2000行2列的数据
join_point = np.concatenate([points, line], axis=0)
plt.scatter(join_point[:, 0], join_point[:, 1], alpha=0.5, color="#ff0000")
# 使横纵坐标等长
plt.axis("equal")
plt.show()
2.2 对点数据进行拉伸旋转平移:
a.仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
b.仿射变换可以进行平移、旋转、放缩、镜像等变化。
c.仿射变换,可以保持原来的线共点、点共线的关系不变,保持原来相互平行的线仍然平行,保持原来的中点仍然是重点,保持原来在一直线上的几段线段的比例关系不变,但是仿射变换不能保持原来的线段长度不变,也不能保持原来夹角角度不变。
d.仿射变换公式:
[ x 1 y 1 1 ] = [ a 1 a 2 t x a 3 a 4 t y 0 0 1 ] ⋅ [ x y 1 ] \begin{bmatrix} x_1\\ y_1 \\ 1\\ \end{bmatrix} = \begin{bmatrix} a_1 & a_2 & t_x \\ a_3 & a_4 & t_y \\ 0 & 0 & 1\\ \end{bmatrix} \cdot \begin{bmatrix} x\\ y \\ 1\\ \end{bmatrix} ⎣⎡x1y11⎦⎤=⎣⎡a1a30a2a40txty1⎦⎤⋅⎣⎡xy1⎦⎤
其 中 ( t x , t y ) 表 示 平 移 量 , 而 参 数 a i 则 反 映 了 图 像 旋 转 、 缩 放 等 变 化 。 其中 (t_x,t_y)表示平移量,而参数a_i则反映了图像旋转、缩放等变化。 其中(tx,ty)表示平移量,而参数ai则反映了图像旋转、缩放等变化。
例如:
"""
仿射变换,拉伸,旋转, 平移
"""
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend("TkAgg")
# 随机生成 1000 行, 2列的范围从 (0-1)的数据
points = np.random.random([1000, 2])
# 生成均匀的1000个 0到2的数字
random_num = np.linspace(0, 2, 1000)
# 将 line_x 重调为 1000行 1 列的矩阵
line_x = np.reshape(random_num, [1000, 1])
# 将 line_x进行列拼接. 得到 1000行两列的数据, 该数据类似于 斜率 0.5的直线
line = np.concatenate([line_x, line_x], axis=1)
# 将散点和线性数据进行 行拼接, 得到 2000行2列的数据
join_point = np.concatenate([points, line], axis=0)
# 设置一个转换器(2行2列的矩阵), 该变换是 x 轴方向拉伸
# 该矩阵的行列式也代表了面积的变化, 比如该行列式的为2,则代表变化后, 面积扩大了一倍
A1 = np.array([[2, 0],
[0, 1]])
# 进行仿射变换, 以下三种均为矩阵的点乘
# affine_point = join_point.dot(A)
# affine_point = np.dot(join_point, A)
affine_point1 = join_point @ A1
# 设置一个转换器(2行2列的矩阵),该变换是斜向拉伸
A2 = np.array([[1, 0.5],
[0.5, 1]])
affine_point2 = join_point @ A2
# 单位矩阵, 做乘法保持以前大小形状角度不变
A3 = np.array([[1, 0],
[0, 1]])
# 平移矩阵, 标识向右平移1, 向上平移2
B = np.array([1, 2])
affine_point3 = join_point @ A3 + B
# 将原图形旋转90度
theta = np.pi/2
A4 = np.array([[np.cos(theta), np.sin(theta)],
[-np.sin(theta), np.cos(theta)]])
affine_point4 = join_point @ A4
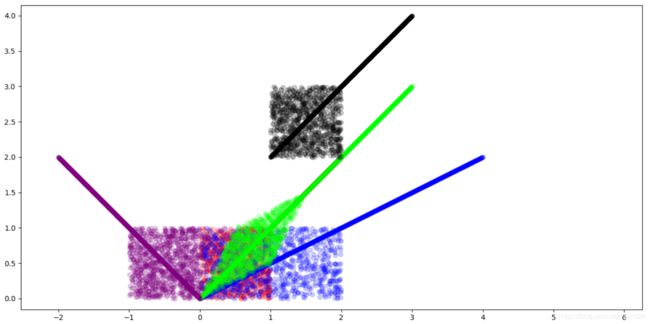
plt.scatter(join_point[:, 0], join_point[:, 1], alpha=0.2, color="#ff0000")
plt.scatter(affine_point1[:, 0], affine_point1[:, 1], alpha=0.2, color="#0000ff")
plt.scatter(affine_point2[:, 0], affine_point2[:, 1], alpha=0.2, color="#00ff00")
plt.scatter(affine_point3[:, 0], affine_point3[:, 1], alpha=0.2, color="#000000")
plt.scatter(affine_point4[:, 0], affine_point4[:, 1], alpha=0.2, color="#800080")
# 使横纵坐标等长
plt.axis("equal")
plt.show()
三. 利用仿射变换可以对图像进行操作
"""
将姚明同学逆过来
"""
import cv2
import numpy as np
# 获取图片并获取宽高信息
img = cv2.imread("ym.png")
h, w, c = img.shape
# openCV的参数设置中, A和B写在了一起
# 以y轴为标准做镜像, 并平移宽度 w的长度
A = np.array([[-1., 0., w],
[0., 1, 0]])
img = cv2.warpAffine(img, A, (w, h))
cv2.imshow("img", img)
cv2.waitKey(0)
四.对视频进行仿射变换
例如:
import cv2
import numpy as np
# 读取摄像的句柄,调去第一个摄像头
cap = cv2.VideoCapture(0)
# 构建读取循环
while True:
ret, img = cap.read()
h, w, c = img.shape
# 对影像做仿射变换
A = np.array([[-1., 0., w],
[0., 1, 0]])
img = cv2.warpAffine(img, A, (w, h))
cv2.imshow("img", img)
# 每隔100ms没响应则继续读取
ret = cv2.waitKey(100)
if ret == 97:
break
cv2.destroyAllWindows()